KMP模式匹配算法

朴素的模式匹配算法

对主串的每一个字符作为子串的开头，与要匹配的字符串进行匹配。对主串做大循环，每个字符开头做需匹配长度的小循环，直到匹配成功或者全部遍历完成为止

示例程序(朴素的模式匹配)

int Index(char *S, char *T)
{
    int i, j;
    // 直到遍历主串完成或者需匹配字符串全部匹配成功
    for (i = 0, j = 0; i < (int)strlen(S) && j < (int)strlen(T);) {
        if (S[i] == T[j]) {
            // 如果当前字符相同，则比较下一个字符
            i++;
            j++;
        } else {
            // 如果当前字符不同，则主串进行回溯，跳转到当前匹配的开头的下一位
            // 需匹配字符串从头开始
            i = i - j + 1;
            j = 0;
        }
    }
    // 判断是否全部匹配成功，返回位置(第)
    if (j == (int)strlen(T)) {
        return i - j + 1;
    } else {
        return -1;
    }
}

---

KMP模式匹配算法

按照朴素的模式匹配算法进行字符串的查找，我们仔细想想会发现，有些步骤是多余的，例如：

主串S:abcfgex
需要匹配串T:abcx

第1次:
abcdefgex
abcdex
i=6,j=6,f和x不相等

第2次:
abcdefgex
 abcdex
i=2,j=1,a和b不相等

第3次:
abcdefgex
  abcdex
i=3,j=1,a和c不相等

第4次:
abcdefgex
   abcdex
i=4,j=1,a和d不相等

第5次:
abcdefgex
    abcdex
i=5,j=1,a和e不相等

第6次:
abcdefgex
     abcdex
i=6,j=1,a和f不相等

仔细分析可以发现，在第一次匹配中，我们已经知道S和T的abcde是一样的，而且T串的首字符与后面的字符均不相同，所以其实第2,3,4,5次匹配是多余的，第6次由于S和T不相同，不能判断T的首字符是否与S不同，固从第6次开始继续比较即可

那么可能有人又要问了，假如T串后面也有字符a那该怎么办呢?

接下来我们看看下面的例子:

主串S:abcababcacc
需要匹配串T:abcabx

第1次:
abcababcacc
abcabx
i=6,j=6,x和a不相等

第2次:
abcababcacc
 abcabx
i=2,j=1,a和b不相等

第3次:
abcababcacc
  abcabx
i=3,j=1,a和c不相等

第4次:
abcababcacc
   abcabx
i=6,j=3,c和a不相等

同样，我们可以发现2,3,5是多余的，而且第4次中ab的比较也是多余的，因为在1中已经比较ST中12的ab和45的ab均是相同的，已经比较过，固不需要再回溯比较

继续分析我们可以发现，很多回溯都是没有必要的，那么KMP算法出现了，KMP算法的目的就是为了减少没必要的回溯，为了方便分析，我们将上面两个例子去除没必要的回溯，如下:

主串S:abcfgex
需要匹配串T:abcx

第1次:
abcdefgex
abcdex
i=6,j=6,f和x不相等

第6次:
abcdefgex
     abcdex
i=6,j=1,a和f不相等

主串S:abcababcacc
需要匹配串T:abcabx

第1次:
abcababcacc
abcabx
i=6,j=6,x和a不相等

第4次:
abcababcacc
   abcabx
i=6,j=3,c和a不相等

既然主串中i值不回溯，也就是i不能变小，那么我们要考虑的当然也就是T串中的j值了，而且通过上面的分析我们可以发现T串中j值的变化与主串无关，而是与自身是否有重复串有关。例如上面的例子，在例子一中，T中没有重复的字符，j直接由6变为1，在例子二中由于前缀ab与后缀ab相同，j由6变为3

这时要引入一个辅助next数组，来保存j的变化值，也就是说next数组其实就是查找T串中每一位前面的子串的前后缀有多少位匹配，从而决定j失配时应该回退到哪个位置。

next数组值的推导

函数定义：

• j = 0时, next[j] = -1
• 如果对于值k，已有p0 p1, …, pk-1 = pj-k pj-k+1, …, pj-1，相当于next[j] = k。即若0到j-1的子串前缀后缀的公共元素的最大长度n, next[j] = n

推导分析：

j	0	1	2	3	4	5
String T	a	b	c	d	e	f
next[j]	-1	0	0	0	0	0

j	0	1	2	3	4	5
String T	a	b	c	a	b	x
next[j]	-1	0	0	0	1	2

j	0	1	2	3	4	5
String T	a	b	a	b	a	b
next[j]	-1	0	0	1	2	3

j	0	1	2	3	4	5
String T	a	a	a	a	a	a
next[j]	-1	0	1	2	3	4

接下来要做的工作，我们需要深入理解一下next数组的含义，对于next函数的理解也是整个KMP算法的关键所在，也是整个KMP算法的核心，所以我们必须深刻的理解它的含义

现在我们要解决的问题是已知next [0, …, j]，如何求出next [j + 1]呢？

模式字符串记为P(下标从0开始)，next[q] = k 表示P[q]之前的子串中，存在长度为k的相同前缀和后缀，即P[0]~P[k-1]与P[q-k]~P[q-1]依次相同。如果P[k] = P[q]，那么next[q+1] = k+1，此时表示P[q+1]之前的子串中，存在长度为k+1的相同前后缀，这应该不成问题。下面贴张图详细表示：

如果P[k] != P[q]，那么说明next[q+1] 不会是 k+1，也就是说P[q+1]之前的子串中，不会存在长度为k+1的相同前后缀。那么我们就要去寻找长度更短的相同前后缀，假设长度为j，此时P[0]~P[j-1]和P[q-j]~P[q-1]依次相同。下面再贴张图：

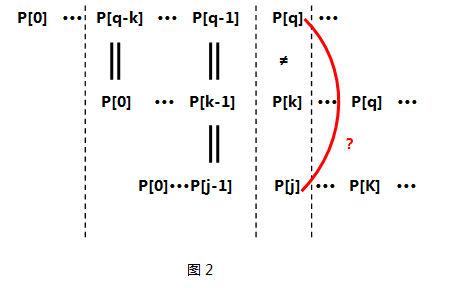
接着我们比较P[q]和P[j]是否相同，如果相同，则next[q+1] = j+1；如果不同，则按照k = next[k]递归查找。说到这，大家应该可以看出这里的j = next[k]。如果还不明白，看看next数组的定义，next[k] = j 表示P[k]之前的子串中，存在长度为j的相同前后缀。从图2可以看出，P[0]~P[j-1]和P[k-j]~P[k-1]是依次相同的

next数组获取代码

int GetNext(char *T, int *next)
{
    int i, j;
    // 初始化next数组，方便调试输出，可去除
    for (i = 0; i < 255; i++) {
        next[i] = -255;
    }
    // 初始化第1位数据
    next[0] = -1;
    for (i = 0, j = -1; i < (int)strlen(T) - 1;) {
        if (j == -1 || T[i] == T[j]) {
            // T[i]表示后缀的单个字符，T[j]表示前缀的单个字符
            next[++i] = ++j;
        } else {
            // j值回溯
            j = next[j];
        }
    }
    return 0;
}

等我深入理解了再回头来整理一下

有了next数组以后，我们可以进行KMP匹配：

int IndexKMP(char *S, char *T)
{
    int i, j;
    int next[256];
    GetNext(T, next);
    // PrintNext(next);
    for (i = 0, j = 0; i < (int)strlen(S) && j < (int)strlen(T);) {
        // 新增j==0判断
        if (j == 0 || S[i] == T[j]) {
            i++;
            j++;
        } else {
            // i值不需要回溯，j值跳到预设的位置
            j = next[j];
        }
    }
    if (j == (int)strlen(T)) {
        return i - j + 1;
    } else {
        return -1;
    }
}

完整代码

/*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

  > Author: xiaojunyu/LunaW
  > Mail  : [email protected]
  > Gmail : [email protected]
  > Blog  : http://blog.csdn.net/lunaw
  > Web   : http://lunaw.cn

 *-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*/

#include 
#include 

int Index(char *S, char *T);    // 朴素模糊匹配 返回子串的位置
int GetNext(char *T, int *next);    // KMP模式匹配中next数组的获取
int PrintNext(int *next);   // 打印next数组
int IndexKMP(char *S, char *T); // KMP匹配算法 返回子串的位置

int main(void)
{
    char S[] = "1234512125";
    char T[] = "12125";
    // printf("%d\n", Index(S, T));
    printf("%d\n", IndexKMP(S, T));
    return 0;
}

int PrintNext(int *next)
{
    int i;
    for (i = 0; next[i] != -255; i++) {
        printf("%d ", next[i]);
    }
    printf("\n");
    return 0;
}

int GetNext(char *T, int *next)
{
    int i, j;
    // 初始化next数组，方便调试输出，可去除
    for (i = 0; i < 255; i++) {
        next[i] = -255;
    }
    // 初始化第1位数据
    next[0] = -1;
    for (i = 0, j = -1; i < (int)strlen(T) - 1;) {
        if (j == -1 || T[i] == T[j]) {
            // T[i]表示后缀的单个字符，T[j]表示前缀的单个字符
            next[++i] = ++j;
        } else {
            // j值回溯
            j = next[j];
        }
    }
    return 0;
}

int Index(char *S, char *T)
{
    int i, j;
    // 直到遍历主串完成或者需匹配字符串全部匹配成功
    for (i = 0, j = 0; i < (int)strlen(S) && j < (int)strlen(T);) {
        if (S[i] == T[j]) {
            // 如果当前字符相同，则比较下一个字符
            i++;
            j++;
        } else {
            // 如果当前字符不同，则主串进行回溯，跳转到当前匹配的开头的下一位
            // 需匹配字符串从头开始
            i = i - j + 1;
            j = 0;
        }
    }
    // 判断是否全部匹配成功，返回位置(第)
    if (j == (int)strlen(T)) {
        return i - j + 1;
    } else {
        return -1;
    }
}

int IndexKMP(char *S, char *T)
{
    int i, j;
    int next[256];
    GetNext(T, next);
    // PrintNext(next);
    for (i = 0, j = 0; i < (int)strlen(S) && j < (int)strlen(T);) {
        // 新增j==0判断
        if (j == 0 || S[i] == T[j]) {
            i++;
            j++;
        } else {
            // i值不需要回溯，j值跳到预设的位置
            j = next[j];
        }
    }
    if (j == (int)strlen(T)) {
        return i - j + 1;
    } else {
        return -1;
    }
}

---

KMP算法优化

待后续完全理解了再进行完善