分治法及经典例题
分治法的基本思想
将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治法的求解过程:
①划分:将整个问题划分为多个子问题,子问题与原问题有相同的类型。
②求解:求解各个子问题(可以使用递归反复调用)
③合并:合并所有子问题的解,形成原问题的解。

分治算法经典例题1:二分查找
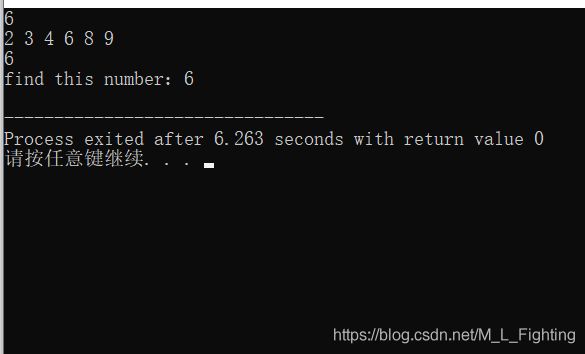
给定一个有序数组,查找某数是否在这个有序数组中。
#include结果展示:
分治算法经典例题2:求数组中的最大最小值
#include结果展示:
分治算法经典例题3:快速排序
#include