Collections中sort()和Arrays中的sort方法分析

首先从源代码看起：

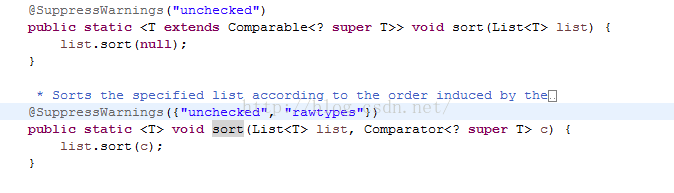
在Collections中提供的sort方法有以下有两种重载

第一个重载的定义是：> 表示该方法中传递的泛型参数必须实现了Comparable中的compareTo(T o)方法，否则进行不了sort排序。第二个是提供Comparator（比较手段）。

然后再来看list.sort(c)这个方法：

default void sort(Comparator c) {
        Object[] a = this.toArray();
        Arrays.sort(a, (Comparator) c);
        ListIterator i = this.listIterator();
        for (Object e : a) {
            i.next();
            i.set((E) e);
        }
    }

把这个方法细分为3个步骤：

（1）将list装换成一个对象数组

（2）将这个对象数组传递给Arrays类的sort方法（也就是说collections的sort其实本质是调用了Arrays.sort）

（3）完成排序之后，再一个一个地，把Arrays的元素复制到List中。

那么我们自然地来追溯Arrays类的sort方法：（重点看一下如下两个重载（归并排序，优化后的归并排序），其他还有其他类型参数的重载（使用的快排），但都能理解）

public static void sort(Object[] a) {
        if (LegacyMergeSort.userRequested)
            legacyMergeSort(a);
        else
            ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
    }

 public static  void sort(T[] a, Comparator c) {
        if (c == null) {
            sort(a);
        } else {
            if (LegacyMergeSort.userRequested)
                legacyMergeSort(a, c);
            else
                TimSort.sort(a, 0, a.length, c, null, 0, 0);
        }
    }

重点在于： sort有一个分支判断，当LegacyMergeSort.userRequested为true的情况下，采用legacyMergeSort，否则采用ComparableTimSort。LegacyMergeSort.userRequested的字面意思大概就是“用户请求传统归并排序”的意思，这个分支调用的是与jdk1.5相同的方法来实现功能。

ComparableTimSort是改进后的归并排序，对归并排序在已经反向排好序的输入时表现为O(n^2)的特点做了特别优化。对已经正向排好序的输入减少回溯。对两种情况（一会升序，一会降序）的输入处理比较好（摘自百度百科）。

legacyMergeSort方法最终调用的是如下mergeSort方法，下面来看一下mergeSort：

private static void mergeSort(Object[] src,
                                  Object[] dest,
                                  int low,
                                  int high,
                                  int off) {
        int length = high - low;

        // Insertion sort on smallest arrays
        if (length < INSERTIONSORT_THRESHOLD) {
            for (int i=low; ilow &&
                         ((Comparable) dest[j-1]).compareTo(dest[j])>0; j--)
                    swap(dest, j, j-1);
            return;
        }

        // Recursively sort halves of dest into src
        int destLow  = low;
        int destHigh = high;
        low  += off;
        high += off;
        int mid = (low + high) >>> 1;
        mergeSort(dest, src, low, mid, -off);
        mergeSort(dest, src, mid, high, -off);

        // If list is already sorted, just copy from src to dest.  This is an
        // optimization that results in faster sorts for nearly ordered lists.
        if (((Comparable)src[mid-1]).compareTo(src[mid]) <= 0) {
            System.arraycopy(src, low, dest, destLow, length);
            return;
        }

        // Merge sorted halves (now in src) into dest
        for(int i = destLow, p = low, q = mid; i < destHigh; i++) {
            if (q >= high || p < mid && ((Comparable)src[p]).compareTo(src[q])<=0)
                dest[i] = src[p++];
            else
                dest[i] = src[q++];
        }
    }

注：INSERTIONSORT_THRESHOLD常量为7，当排序数组长度小于7则使用插入排序（小数组使用插入排序），当大于7时使用我们通常的归并排序（递归与合并两个过程）。

• ComparableTimSort.sort()方法的代码：

• static void sort(Object[] a, int lo, int hi, Object[] work, int workBase, int workLen) {
          assert a != null && lo >= 0 && lo <= hi && hi <= a.length;
  
          int nRemaining  = hi - lo;
          if (nRemaining < 2)
              return;  // Arrays of size 0 and 1 are always sorted
  
          // If array is small, do a "mini-TimSort" with no merges
          if (nRemaining < MIN_MERGE) {
              int initRunLen = countRunAndMakeAscending(a, lo, hi);
              binarySort(a, lo, hi, lo + initRunLen);
              return;
          }
  
          /**
           * March over the array once, left to right, finding natural runs,
           * extending short natural runs to minRun elements, and merging runs
           * to maintain stack invariant.
           */
          ComparableTimSort ts = new ComparableTimSort(a, work, workBase, workLen);
          int minRun = minRunLength(nRemaining);
          do {
              // Identify next run
              int runLen = countRunAndMakeAscending(a, lo, hi);
  
              // If run is short, extend to min(minRun, nRemaining)
              if (runLen < minRun) {
                  int force = nRemaining <= minRun ? nRemaining : minRun;
                  binarySort(a, lo, lo + force, lo + runLen);
                  runLen = force;
              }
  
              // Push run onto pending-run stack, and maybe merge
              ts.pushRun(lo, runLen);
              ts.mergeCollapse();
  
              // Advance to find next run
              lo += runLen;
              nRemaining -= runLen;
          } while (nRemaining != 0);
  
          // Merge all remaining runs to complete sort
          assert lo == hi;
          ts.mergeForceCollapse();
          assert ts.stackSize == 1;
      }

  
  （1）传入的待排序数组若小于阈值MIN_MERGE（Java实现中为32，Python实现中为64），则调用 binarySort，这是一个不包含合并操作的mini-TimSort。（binarySort的解释： Sorts the specified portion of the specified array using a binary insertion sort.  This is the best method for sorting small numbers of elements.  It requires O(n log n) compares, but O(n^2) data movement (worst case).）
  
• a) 从数组开始处找到一组连接升序或严格降序（找到后翻转）的数 
  b) Binary Sort：使用二分查找的方法将后续的数插入之前的已排序数组，binarySort 对数组 a[lo:hi] 进行排序，并且a[lo:start]是已经排好序的。算法的思路是对a[start:hi] 中的元素，每次使用binarySearch 为它在 a[lo:start] 中找到相应位置，并插入。
  
• （2）开始真正的TimSort过程：
  
• （2.1） 选取minRun大小，之后待排序数组将被分成以minRun大小为区块的一块块子数组，如下是minRunLength方法的源码：

   private static int minRunLength(int n) {
          assert n >= 0;
          int r = 0;      // Becomes 1 if any 1 bits are shifted off
          while (n >= MIN_MERGE) {
              r |= (n & 1);
              n >>= 1;
          }
          return n + r;
      }

  解释：a) 如果数组大小为2的N次幂，则返回16（MIN_MERGE / 2） b) 其他情况下，逐位向右位移（即除以2），直到找到介于16和32间的一个数。这个函数根据 n 计算出对应的 natural run 的最小长度。MIN_MERGE 默认为32，如果n小于此值，那么返回n 本身。否则会将 n 不断地右移，直到少于 MIN_MERGE，同时记录一个 r 值，r 代表最后一次移位n时，n最低位是0还是1。 最后返回 n + r，这也意味着只保留最高的 5 位，再加上第六位。

• （2.2）do-while

  （2.2.1）找到初始的一组升序数列，countRunAndMakeAscending 会找到一个run ，这个run 必须是已经排序的，并且函数会保证它为升序，也就是说，如果找到的是一个降序的，会对其进行翻转。

  （2.2.2）若这组区块大小小于minRun，则将后续的数补足，利用binarySort 对 run 进行扩展，并且扩展后，run 仍然是有序的。

  （2.2.3）当前的 run 位于 a[lo:runLen] ，将其入栈ts.pushRun(lo, runLen);//为后续merge各区块作准备：记录当前已排序的各区块的大小

  （2.2.4）对当前的各区块进行merge，merge会满足以下原则（假设X，Y，Z为相邻的三个区块）：

  a) 只对相邻的区块merge 
  b) 若当前区块数仅为2，If X<=Y，将X和Y merge 
  b) 若当前区块数>=3，If X<=Y+Z，将X和Y merge，直到同时满足X>Y+Z和Y>Z

  由于要合并的两个 run 是已经排序的，所以合并的时候，有会特别的技巧。假设两个 run 是 run1,run2 ，先用 gallopRight在 run1里使用 binarySearch 查找run2 首元素 的位置k, 那么 run1 中 k 前面的元素就是合并后最小的那些元素。然后，在run2 中查找run1 尾元素 的位置 len2 ，那么run2 中 len2 后面的那些元素就是合并后最大的那些元素。最后，根据len1 与len2 大小，调用mergeLo或者 mergeHi 将剩余元素合并。

  （2.2.5） 重复2.2.1 ~ 2.2.4，直到将待排序数组排序完  
  （2.2.6） Final Merge：如果此时还有区块未merge，则合并它们