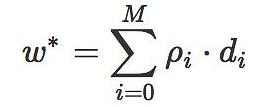【机器学习】GBDT 算法 整理

GBDT是一种集成学习算法，却和传统的Adaboost有很大的不同。回顾下Adaboost，它是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同（备注：Adaboost我会再新开日记）。

CART决策树既可以用于分类也可以用于回归，决策树分为分类树和回归树，分类树的衡量标准是最大熵，回归树的衡量标准是最小化均方差，所以GBDT中的树都是回归树，不是分类树，这点对理解GBDT相当重要（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。

GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

对于机器学习来说，监督学习就是训练数据既有特征(feature)又有标签(label)，通过训练，让算法可以自己找到特征和标签之间的联系，即训练模型，在面对只有特征没有标签的数据时，用已训练的模型，可以判断出标签。监督学习主要运用于分类算法。

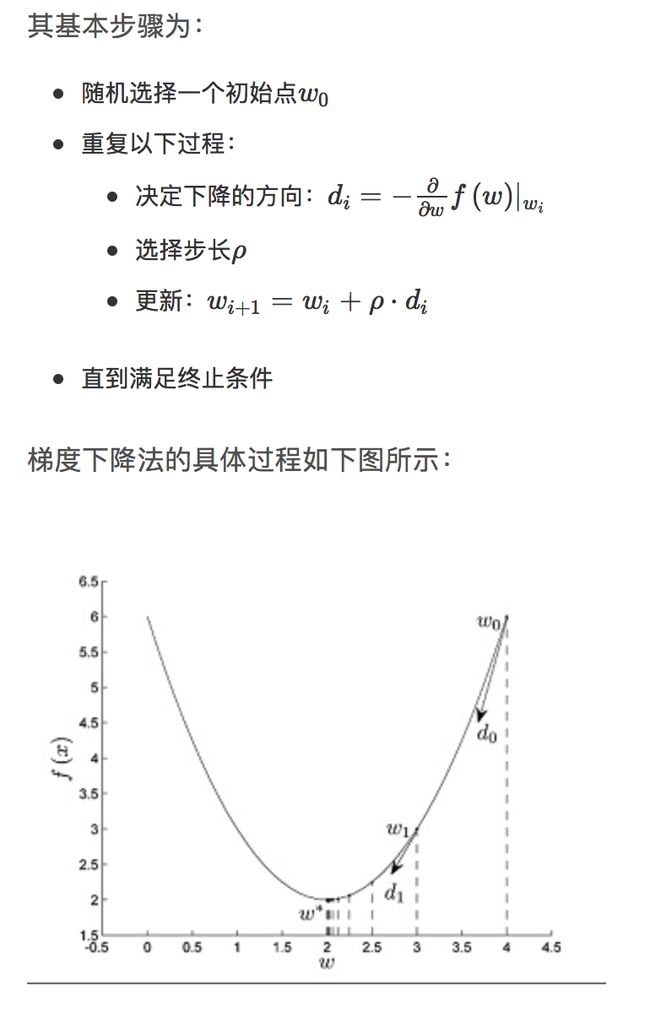
参考梯度下降法的思路，相同的处理过程，不同的处理对象。 梯度下降算法是求解最优化问题最简单、最直接的方法。梯度下降法是一种迭代的优化算法，对于优化损失函数问题： min f(w)

网络截图，非原创

由以上的过程，我们可以看出，对于最终的最优解w∗，是由初始值w0经过M代的迭代之后得到的，在这里，设w0=d0，则w∗为：

以上是在指定的函数空间中对最优函数进行搜索，结果是搜索到一个最优的w，那么，能否直接在函数空间（function space）中查找到最优的函数呢？根据上述的梯度下降法的思路，对于模型的损失函数L(y,F(X))，为了能够求解出最优的函数F∗(X)，首先，设置初始值为：

F0(X)=f0(X)

以函数F(X)作为一个整体，对于每一个样本X(i)，都存在对应的函数值F(X(i))。与梯度下降法的更新过程一致，假设经过M代，得到最优的函数F∗(X)为：

gm(X)是决定下降的方向(可理解为矢量，是有方向、长度的值)，pi是下降的步长。这里h(X;a)与gm(X)是同一个函数不同表示，h(X;a)中有L(y,F(X))，F(X)有参数a，这里的a可理解为一般梯度下降处理时的w。 梯度下降是优化一个损失函数，处理的粒度是更新参数w，使得最后的损失函数f(w)最小，f(w)也可以表示为L(y,f(x))； 函数空间的优化也是梯度下降的思路，处理粒度是更新函数F∗(X)，使得损失函数L(y,F(X))最小。

5，Bagging与Boosting

Boosting的详细原理可以参考另外一篇关于Adboosting的介绍。这里做两者对比，这部分内容主要是复制某个博客的内容，因为说的太好了。 Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器，更准确的说这是一种分类算法的组装方法。即将弱分类器组装成强分类器的方法。 首先介绍Bootstraping，即自助法：它是一种有放回的抽样方法（可能抽到重复的样本）。 5.1、Bagging (bootstrap aggregating)

Bagging即套袋法，其算法过程如下：

A）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（同一个样本可能被多次抽到）

B）每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

C）对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题：计算上述模型的均值作为最后的结果。（所有模型的重要性相同，每个模型的权值相同）

5.2、Boosting

其主要思想是将弱分类器组装成一个强分类器。在PAC（概率近似正确）学习框架下，则一定可以将弱分类器组装成一个强分类器。

关于Boosting的两个核心问题：

1）在每一轮如何改变训练数据的权值或概率分布？

通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得被误分类的样本重要性提高，促使分类器对误分的数据有较好的效果或者说让那些能正确把之前被误分类的样本准确分类的模型的权值提高。

2）通过什么方式来组合弱分类器？

通过加法模型将弱分类器进行线性组合，比如AdaBoost通过加权多数表决的方式，即增大错误率小的分类器的权值，同时减小错误率较大的分类器的权值。 而提升树通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型。

5.3、Bagging，Boosting二者之间的区别

Bagging和Boosting的区别：

1）样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

Bagging：使用均匀取样，每个样例的权重相等

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

Bagging：各个预测函数可以并行生成

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

5)、总结

这两种方法都是把若干个分类器整合为一个分类器的方法，只是整合的方式不一样，最终得到不一样的效果，将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果，但是也增大了计算量。

下面是将决策树与这些算法框架进行结合所得到的新的算法：

（1）Bagging + 决策树 = 随机森林

（2）AdaBoost + 决策树 = 提升树

（3）Gradient Boosting + 决策树 = GBDT 转自：https://blog.csdn.net/u014755493/article/details/70225437

6，Gradient Boosting

boosting是一种思想，Gradient Boosting是一种实现Boosting的方法，它的主要思想是，每一次建立模型，是在之前建立模型损失函数的梯度下降方向。损失函数描述的是模型的不靠谱程度，损失函数越大，说明模型越容易出错。如果我们的模型能够让损失函数持续的下降，说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度的方向下降。 一般的梯度下降是以一个样本点(xi,yi)作为处理的粒度，w是参数，f(w;x)是目标函数，即减小损失函数L(yi,f(xi;w))，优化过程就是不断处理参数w(这里用到梯度下降)，使得损失函数L最小；GB是以一个函数作为处理粒度，对上一代的到的函数或者模型F(X)求梯度式，即求导，决定下降方向。 请参考第4部分——在函数空间的优化。

7，Gradient Boosting Decision Tree

GBDT的决策树有两种回归树和分类树，具体的决策树可以是CART或者C4.5生成。GBDT可以是学习得到一个强学习器f(x)，这样是通过梯度下降学习的，预测一个数值，这样的数值是连续的；也可以预测一个实数值，例如：10岁，20岁，5岁等，这样的数值是离散的；以上两种可以称为是回归时的功能。分类树是用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。这里要强调的是，前者的结果加减是有意义的，如10岁+5岁-3岁=12岁，后者则无意义，如男+男+女=到底是男是女？要强调的是：不管是预测数值还是分类，在GBDT中都是学习残差的过程。

1）下面先介绍回归树梯度下降求解法

 

弱分类器ht(x)的生成是拟合一个与上一代的损失函数相关的函数

 

用(xi,rti)拟合的回归树是根据输入x和上一轮残差rti计算得来的，结果是得到ctj，其中的ft-1(x)是上一代(t-1代)的学习器。ctj公式意思是：本轮决策树加入参数c，拟合上一轮残差rti，并使得拟合时误差最小情况下得到的输出是ctj。本轮拟合残差rti的结果是ctj

ctj的表达式意思是拟合上一轮的残差，拟合过程中误差最小情况下输出的拟合结果，拟合上一轮ft-1(x)与yi之间的残差rti，ht(x)是目标函数。这个目标函数是要用到本轮最终的强学习器中。J是指多个节点，每个节点中的样本计算值与目标值之间邪恶差距是不同的，所以上一轮的残差不同，本轮拟合残差的结果不同，要分开。

想想在线性回归中，例如我们希望找到一组参数使得模型的残差最小化。如果只使用一次项来解释二次曲线，那么就会存有大量残差，此时就可以用二次项来继续解释残差，所以可在模型中加入这个二次项，得出结果与目标值之间的差会减小。

2）分类树：学习残差

 

网络截图1

 

网络截图2

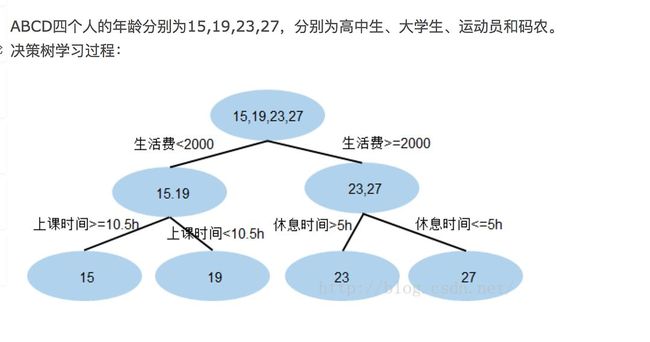
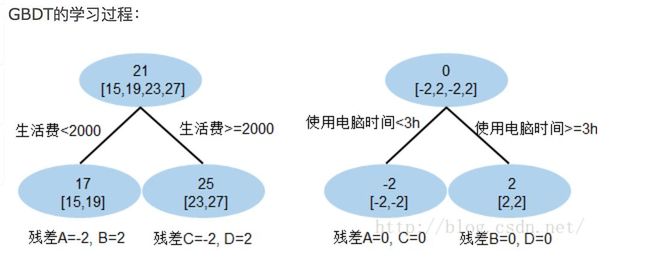
现在A,B,C,D的预测值都和真实年龄一致 A: 15岁高中学生，收入较少，天天没时间玩电脑；预测年龄A = 17– 2 = 15

B: 19岁大学生；收入较少，天天宅在宿舍玩电脑；预测年龄B = 17+ 2 = 19

C: 23岁运动员；收入较多，体育训练没时间玩电脑；预测年龄C = 25 – 2 = 23

D: 27岁码农；收入较多，长时间玩电脑；预测年龄D = 25 + 2 = 27

注：图1和图2最终效果相同，为何还需要GBDT呢，答案是过拟合。过拟合是指为了让训练准确率更高，在训练集范围内的准确率很高，但是泛化性很低，换一个数据集，模型就失效了。只要允许一棵树的叶子结点足够多，训练集的准确率总会到100%的。在训练准确度和实际预测准确度之间，大家肯定选择后者。

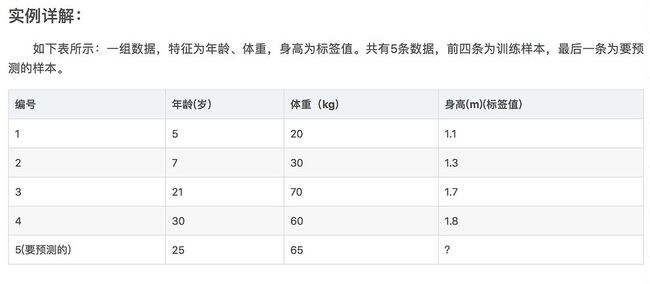
8，GBDT实例

上文已经说了一个例子了，这个例子即前文说的学习残差，不是通过梯度下降的方式。事实上本文说的梯度下降或者学习残差都是相同原理。 接下来介绍梯度下降相关的简单实例：

网络截图

 

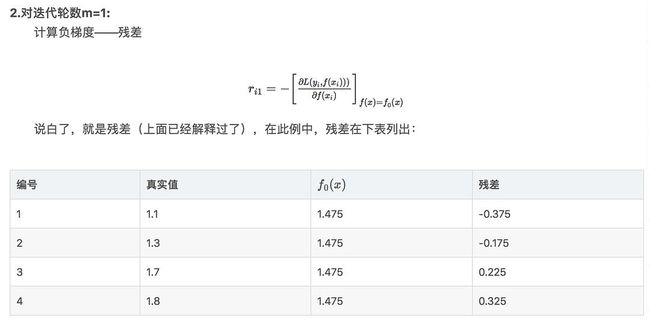
这里r就是前文公式中的c；在对r求偏导数时，是对每个样本求偏导数，即(r-y1)+(r-y2)+(r-y3)+(r-y4)=0,结果r是y的平均数

 

网络截图

 

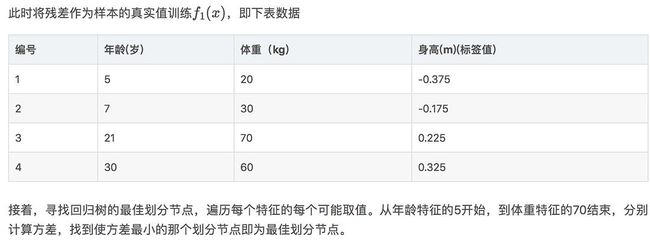
将根节点划分为两个节点，与真实身高之间的差就是残差需要下一轮学习。计算方差的方式就是划分之后的节点，节点里的值先求均值，再求方差。网络截图3

 

这里说的方差就是指求平均值然后求平均差值

 

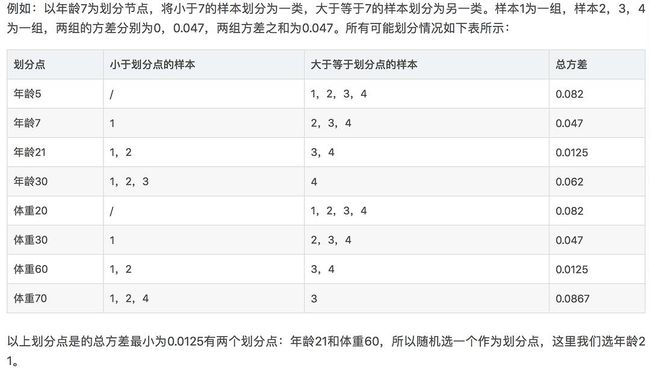
这里说的拟合残差是指拟合网络截图3中的身高残差，和求f0(x)一样是求平均值。这里的r就是前文的ctj，就是下标不同;f0(x)就是前文的ft-1(x)。根据总方差最小根节点分出两个节点，节点1有残差-0.375和-0.175；节点2有残差0.225和0.325。分成两区域j=1

r11和r21与f0(x)相加后与每个样本真实身高之间的差值是新的残差，需要下一轮学习。

网络截图

 

 

9，GBDT与Xgboost的区别

GBDT核心是累加所有树的结果作为最终结果，所以在GBDT中的树可以理解为都是回归树。 回归树的分裂结点对于平方损失函数，拟合的就是残差；对于一般损失函数（梯度下降），拟合的就是残差的近似值，分裂结点划分时枚举所有特征的值，选取划分点。 最后预测的结果是每棵树的预测结果相加。 xgboost算法的步骤和GB基本相同，都是首先初始化为一个常数，gbdt是根据一阶导数ri，xgboost是根据一阶导数gi和二阶导数hi，迭代生成基学习器，相加更新学习器。其他差别在这里只列出部分，这些都是易于理解的，为XGBoost的介绍做铺垫。 基分类器的选择：传统GBDT以CART作为基分类器，XGBoost还支持线性分类器，这个时候XGBoost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。 二阶泰勒展开：传统GBDT在优化时只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，XGBoost工具支持自定义损失函数，只要函数可一阶和二阶求导。 方差-方差权衡：XGBoost在目标函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出分数的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是XGBoost优于传统GBDT的一个特性。 Shrinkage（缩减）：相当于学习速率（xgboost中的）。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）