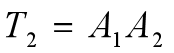Robotics与机器人基础(一):正逆运动学与机械臂搭建
摘要:本文基于Robotics工具箱,结合机器人运动基础,用matlab搭建一个机械臂,并讲述其所需要的运动学知识。
所用环境:Robotics_10.3 matlab_2018a
一、坐标系建立与位姿态计算
每一个连杆具有两个坐标系(注意:坐标系的搭建不是唯一的,不同的坐标系可能导致不同的计算结果,但是都对),我们用一个4x4的齐次变换矩阵来描述不同连杆间的位姿(这里命名为矩阵A)。包括一个旋转变换和一个平移变换,如A1表示第一连杆对基坐标系的位姿。A2表示第二连杆对第一连杆的位姿。则第二连杆对基坐标系的位姿变换矩阵为:
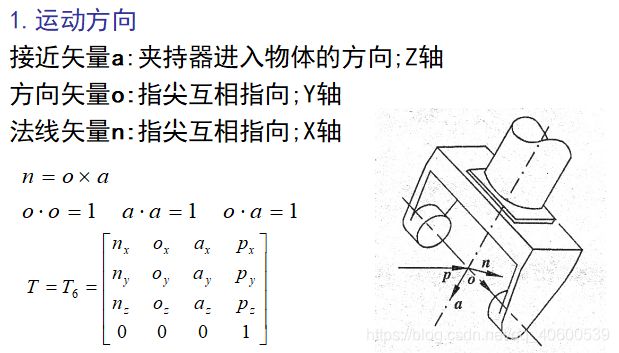
齐次变换矩阵如下。其中n、o、a、p为四个列向量,最后一个描述平移量。
二、描述一台机械臂
机械臂是由一系列串联的连杆组成。在matlab里可通过Link类来构造连杆(后面会介绍)。连杆由关节连接起来,每个关节有一个可以平移(称为移动副)或者旋转(称为转动副)的自由度。
有N个关节的机械臂具有N+1个连杆。连杆0是机械臂的基座,其坐标系称为基坐标系。一个机器人的关节可以由一串字符来表述,R是转动副,P为移动副(R,P可以与之后的robotics函数里一些参数相对应起来)。如Puma560机械臂可以表述为“RRRRRR”,即六个旋转自由度。
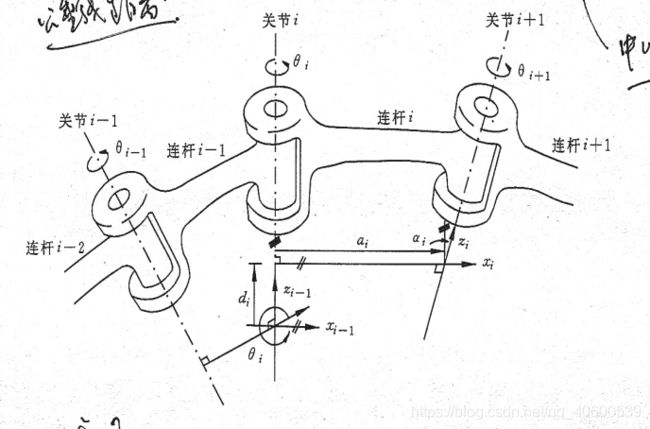
连杆之间具有角度和位移上的不同,从而可以用一些参数描述他们之间的关系,以下是常用的四个参数。与上图对应。
(我认为x坐标轴的选定可以取连杆的轴方向,向右或者向外。当然坐标系选取可以有多种方法)
这些角度、位移参数构成了我们的D-H参数表,有了这个DH表,一个机械手的形状、位姿等就被确定了。
对于转动关节,连杆偏移d是常量;而对于移动关节,关节角是常量。
三、正运动学
即用连杆变换的乘积来求得末端执行机构的位姿。T = A0*A1*A2*…*AN
而位姿矩阵A可以由下列公式求得(可以先旋转再平移,或者平移再旋转;顺序不同得到的结果不同,但是都能达到移动的目的)
四、逆运动学
与正运动学相反,待补充。
五、机械臂的matlab实现
以下基于robotics的环境,需要先下载好。
1、首先是基本的旋转、平移操作
%绕x轴旋转pi/2得到的旋转矩阵
(1)r = rotx(pi/2);
%matlab默认的角度单位为弧度,这里可以用度数作为单位
(2)R = rotx(30, 'deg') * roty(50, 'deg') * rotz(10, 'deg');
%求出R等效的任意旋转变换的旋转轴矢量vec和转角theta
(3)[theta,vec] = tr2angvec(R);
若使用旋转矩阵作为正运动学的算子则要使用trotx等,因为rotx是3*3的矩阵,而trotx返回的是4*4矩阵。
transl(x,y,z) 为平移算子 如:transl(10,0,0) 则代表X正方向上平移10个单位
T = rotz(pi/2)*roty(pi/4)*transl(5,0,0) 可以理解为
①沿原坐标系X轴正方向上平移5个单位,再沿着原坐标y轴旋pi/4,再沿原坐标系z轴旋转(pi/2)。
②沿z轴旋转pi/2,然后沿着新坐标系Y轴旋转pi/4,再沿X轴平移5个单位
即,按原坐标系变换是左乘,按新坐标系变换是右乘算子。
2、连杆绘制
几个连杆和关节就组成了机械手。
连杆可由Link类定义,用法如下:
L1 = Link('d', 0, 'a', 0, 'alpha', pi/2); %Link 类函数,传入'd' =0 ,'a' = 0, 'alpha' = 0;
Link可以传入的参数还有很多,例如:
运动学参数:theta 关节角度;d 连杆偏移量;a 连杆长度;alpha 连杆扭角;等等
动力学参数:m 连杆质量;B 粘性摩擦力(对于电机)1*1或2*2 等等
可通过SerialLink类创建一个机器人对象,把连杆顺序串联成为机械手
bot = SerialLink([L1 L2 L3]);%连接连杆
bot.display();%显示D-H参数表
调用 fkine()函数可以进行正运动学求解,qr数组定义了三个连杆各转动的角度。
qr=[pi/4,pi/4,pi/4]; %终了位置3个关节点的参数
forward_kinematics = fkine(bot,qr);%前向运动学、返回末端变换矩阵调用jtraj(T0,T1,t) 函数可以求从T0到T1的轨迹,用法如下
qr=[pi/4,pi/4,pi/4]; %终了位置3个关节点的参数
t= [0:0.05:2]'; %整个运动发生在2秒内、采样周期是50ms
disp('转动过程中的关节点参数:');
[q,qd,qdd]=jtraj(qz,qr,t);%返回末端位移、速度、加速度3、图像显示
figure()函数可以创建一个图像显示的窗口,显示一副或多图片。
figure('name','hello') 可以定义一个窗口名为’hello'
plot可用于画图。可以理解为figure是一个画布,而plot()传入的才是在画布上显示的图片。例如
bot.plot(q) %显示运动动态轨迹。
创建一个三自由度的连杆机械臂整体代码如下:
clear;clc;
% A = trotz(sita1)*transl(0,0,d1)*transl(a,0,0)*trotx(alpha);
% A = trotz(pi/2)*transl(0,0,0)*transl(0,0,0)*trotx(-pi/2);
L1 = Link('alpha', pi/2, 'a', 2, 'd', 0); %Link 类函数 theta先不传参
L2 = Link('alpha', 0, 'a', 2, 'd', 0);
L3 = Link('alpha', 0, 'a', 1, 'd', 0);
bot = SerialLink([L1 L2 L3]);%连接连杆
bot.display();%显示D-H参数表
qz=[0,0,0]; %初始位置关节点参数
% forward_kinematics = bot.fkine([0 pi/2 pi/2]);%前向运动学
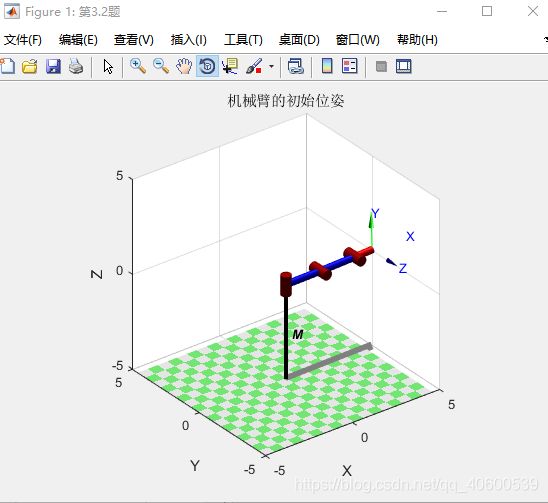
bot.name = 'M';
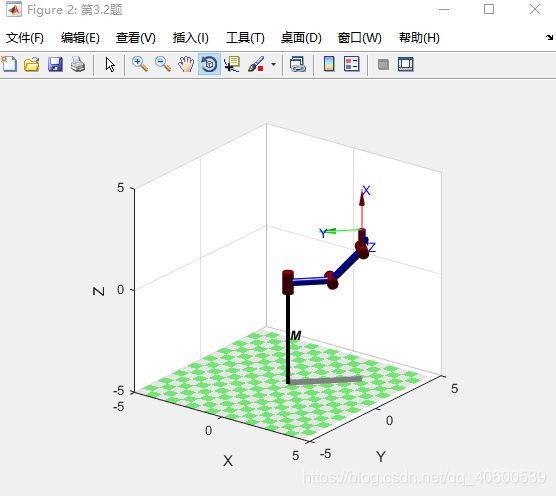
figure('name','第3.2题');
bot.plot([0 0 0]);%绘制机器人
title('机械臂的初始位姿');
%轨迹求解
qr=[pi/4,pi/4,pi/4]; %终了位置3个关节点的参数
forward_kinematics = fkine(bot,qr);%前向运动学、返回末端变换矩阵
t= [0:0.05:2]'; %整个运动发生在2秒内、采样周期是50ms
disp('转动过程中的关节点参数:');
[q,qd,qdd]=jtraj(qz,qr,t);%返回末端位移、速度、加速度
%画动态图
figure('name','第3.2题');
bot.plot(q) %显示运动动态轨迹
title('机械臂运动动态图');
% %以第四个关节点为例画位移,速度,加速度参数变化图
% figure
% %提取矩阵第四列,即为第四个关节点的位移,速度,加速度参数
% i =2;
% q4=q(:,i);
% qd4=qd(:,i);
% qdd4=qdd(:,i);
% subplot(2,2,1)
% plot(t,q4)
% title('位移变化');
% subplot(2,2,2)
% plot(t,qd4)
% title('速度变化');
% subplot(2,2,3)
% plot(t,qdd4)
% title('加速度变化');