逻辑斯蒂回归(Logistic Regression)
本文部分参考和摘录了以下文章,在此由衷感谢以下作者的分享!
周志华《机器学习》
李航《统计学习方法》
通过逻辑回归的sigmoid函数把线性回归转化到[0,1]之间,这个值为什么可以代表概率? - Grok的回答 - 知乎
通过逻辑回归的sigmoid函数把线性回归转化到[0,1]之间,这个值为什么可以代表概率? - 麦田守望者的回答 - 知乎
https://blog.csdn.net/mrxjh/article/details/78499801
logistic回归经常被人译为“逻辑回归“,虽然我个人认为貌似并没有什么关联,但下面就姑且这么叫吧。
逻辑回归虽然是名字里带着回归,但其实是一种解决分类问题的算法,说到分类就有分几类的区别,本篇我们只讨论用于二分类问题的逻辑回归。
基本的线性回归的形式为:
y = ω T x + b y=\omega^{T}x+b y=ωTx+b
线性回归模型产生的预测值是一系列实值。为了使得输出的预测结果变成分类所需的0和1,我们需要在线性回归的基础式子外再套一个函数将其输出变成0和1,我们最理想的函数是单位阶跃函数,单位阶跃函数的图像如下:
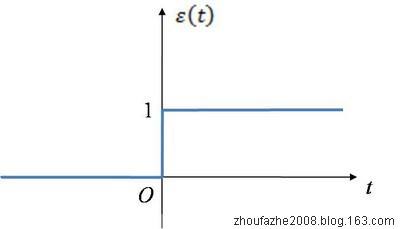
从图中可以看出单位阶跃函数不是连续函数,不连续代表不能保证可微的严格性,因此不能直接作用于式中。我们需要的是一个一定程度上具有相似功能的函数去代替单位阶跃函数,那就是sigmoid函数。sigmoid函数的表达式如下:
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
![]()
sigmoid函数又叫对数几率函数,他能将输出压缩到0-1之内。套上之后的函数表达式为:
y = 1 1 + e − ( ω T x + b ) y=\frac{1}{1+e^{-(\omega^{T}x+b)}} y=1+e−(ωTx+b)1
这样就把线性回归表达式的实值输出结果压缩成了一个0-1之间的小数。但这样还是没有实现分类的效果,我们需要加一个“门槛“,若输出值大于这个门槛,那么就将其结果判断为1,反之判断为0,一般这个“门槛“都是0.5。
从这里我们就可以看出,逻辑回归的输出是有概率意味的,它的输出结果表达的是当前测试样本属于1类别的概率。
当初看完这个算法的介绍后,就有一个问题深深困扰着我,那就是它的输出凭什么能代表概率呢?
我们来看看周志华的《机器学习》中的解释。
由上面的逻辑回归的模型表达式可以推导出:
l n y 1 − y = ω T x + b ln\frac{y}{1-y}=\omega^{T}x+b ln1−yy=ωTx+b
若将 y y y视为样本 x x x作为正例的可能性,则 1 − y 1-y 1−y是其反例的可能性,两者的比值称为“几率“(odds),反映了 x x x作为正例的相对可能性。对几率取对数则得到对数几率:
l n y 1 − y ln\frac{y}{1-y} ln1−yy
这样就可以将上式写为概率形式:
l n P ( y = 1 ∣ x ) P ( y = 0 ∣ x ) = ω T x + b ln\frac{P(y=1|x)}{P(y=0|x)}=\omega^{T}x+b lnP(y=0∣x)P(y=1∣x)=ωTx+b
显然有
P ( y = 1 ∣ x ) = e ω T x + b 1 + e ω T x + b P(y=1|x)=\frac{e^{\omega^{T}x+b}}{1+e^{\omega^{T}x+b}} P(y=1∣x)=1+eωTx+beωTx+b
P ( y = 0 ∣ x ) = 1 1 + e ω T x + b P(y=0|x)=\frac{1}{1+e^{\omega^{T}x+b}} P(y=0∣x)=1+eωTx+b1
(如果不明白这两个式子怎么出来,将第一个式子的分子归一就能得到之前熟悉的表达式)
所以说逻辑回归并不是一个表达式,是两个。用极大似然估计来求出其参数即完成了模型的训练。
以上便是周志华《机器学习》中的推导建模过程。似乎还是没有解释为什么y就能表示概率,只是提到了一句“若将y视为样本作为x正例的可能性“,但并没有严谨的从数学角度解释其原因。
但我从知乎上看到一个解释,再加上自己理解来试着解释一下这个问题。从后验概率再配合贝叶斯公式有如下推导:
P ( c 1 ∣ x ) = P ( x ∣ c 1 ) P ( c 1 ) P ( x ) = P ( x ∣ c 1 ) P c 1 P ( x ∣ c 1 ) P ( c 1 ) + P ( x ∣ c 2 ) P ( c 2 ) = 1 1 + P ( x ∣ c 2 ) P ( c 2 ) P ( x ∣ c 1 ) P ( c 1 ) = 1 1 + e l n P ( x ∣ c 2 ) P ( c 2 ) P ( x ∣ c 1 ) P ( c 1 ) = 1 1 + e − l n P ( x ∣ c 1 ) P ( c 1 ) P ( x ∣ c 2 ) P ( c 2 ) P(c_{1}|x)=\frac{P(x|c_{1})P(c_{1})}{P(x)}\\ \qquad \qquad \qquad \qquad =\frac{P(x|c_{1})P{c_{1}}}{P(x|c_{1})P(c_{1})+P(x|c_{2})P(c_{2})}\\ \quad \qquad =\frac{1}{1+\frac{P(x|c_{2})P(c_{2})}{P(x|c_{1})P(c_{1})}}\\\quad \quad \quad \ =\frac{1}{1+e^{ln\frac{P(x|c_{2})P(c_{2})}{P(x|c_{1})P(c_{1})}}}\\\qquad \quad \ \ \ =\frac{1}{1+e^{-ln\frac{P(x|c_{1})P(c_{1})}{P(x|c_{2})P(c_{2})}}} P(c1∣x)=P(x)P(x∣c1)P(c1)=P(x∣c1)P(c1)+P(x∣c2)P(c2)P(x∣c1)Pc1=1+P(x∣c1)P(c1)P(x∣c2)P(c2)1 =1+elnP(x∣c1)P(c1)P(x∣c2)P(c2)1 =1+e−lnP(x∣c2)P(c2)P(x∣c1)P(c1)1
其中 c 1 c_{1} c1表示第一种情况,也就是类别为1的分类。 P ( c 1 ∣ x ) P(c_{1}|x) P(c1∣x)则表示 x x x为1也就是正例的概率,也就是我们之前推导的 y y y,此时我们会发现最终的推导式子与之前我们列出的逻辑回归的模型表达式非常相似。除了有一点不一样,但是我们稍加推导一下会发现其实也是一样的。
P ( x ∣ c 1 ) P ( c 1 ) P ( x ∣ c 2 ) P ( c 2 ) = P ( x c 1 ) P ( x c 2 ) = P ( c 1 x ) P ( c 2 x ) = P ( c 1 ∣ x ) P ( x ) P ( c 2 ∣ x ) P ( x ) = P ( c 1 ∣ x ) P ( c 2 ∣ x ) = y 1 − y \frac{P(x|c_{1})P(c_{1})}{P(x|c_{2})P(c_{2})}=\frac{P(xc_{1})}{P(xc_{2})}=\frac{P(c_{1}x)}{P(c_{2}x)}=\frac{P(c_{1}|x)P(x)}{P(c_{2}|x)P(x)}=\frac{P(c_{1}|x)}{P(c_{2}|x)}=\frac{y}{1-y} P(x∣c2)P(c2)P(x∣c1)P(c1)=P(xc2)P(xc1)=P(c2x)P(c1x)=P(c2∣x)P(x)P(c1∣x)P(x)=P(c2∣x)P(c1∣x)=1−yy
所以说逻辑回归的模型表达式是有概率的原理在里面的,但前提是 ω T x + b \omega^{T}x+b ωTx+b这个回归表达式拟合的是“对数几率“这种东西。也就是说最终训练出的 ω \omega ω和 b b b要使得这个线性回归表达式的输出为训练样本的对数几率。
那么问题来了,这些样本一定符合这个概率分布吗?这里就是问题所在,我们实现当然不知道它符不符合,所以我们假设他符合,然后直接去做,如果最终的结果是work的,那么说明这假设是成立的,毕竟是必要条件嘛。
如果还是有疑惑的话,那么将这个问题再放大来看,看一下之前推导出来的逻辑回归的概率表达式子:
P ( y = 1 ∣ x ) = e ω T x + b 1 + e ω T x + b P(y=1|x)=\frac{e^{\omega^{T}x+b}}{1+e^{\omega^{T}x+b}} P(y=1∣x)=1+eωTx+beωTx+b
脱开逻辑回归结构这个概念来说,这个式子就是一个概率表达式,我们假设训练样本是符合这个形式的概率分布的,当然这里说的只是这种形式,具体的参数不知道。就如同说样本符合高斯分布,但我们不知道符合具体怎样的高斯分布。
我们就相当于假设训练样本符合这个形式的概率分布,然后通过极大似然估计的方法来找到参数。
其实从极大似然估计的原理也能看出来,极大似然估计的原理就是在已知样本的情况下,去找它最大可能的性的参数是什么,这就是所谓的“极大似然“。
所以说事先我们并不知道样本是否符合这样的概率分布,我们只能假设它符合,然后直接使用看其是否work即可。而数据科学家们会在乎这个假设成立不成立,但做“机器学习“的话就可以直接做了,这也是做“机器学习“的一个鸡贼之处。
接下来我们继续简单推导一下极大似然法估计的去找参数的过程。
对于给定的数据集 { ( x i , y i ) } i = 1 m \{(x_{i},y_{i})\}^{m}_{i=1} {(xi,yi)}i=1m,对率回归模型最大化“对数似然“:
l ( ω , b ) = ∑ i = 1 m l n P ( y i ∣ x i ; ω , b ) l(\omega,b)=\sum_{i=1}^{m}lnP(y_{i}|x_{i};\omega,b) l(ω,b)=i=1∑mlnP(yi∣xi;ω,b)
这个式子的意思是,对于每一个样本来说,找到参数使其属于真实标记的概率最大。
为了便于讨论,令 β = ( ω ; b ) \beta=(\omega;b) β=(ω;b), x ^ = ( x ; 1 ) \widehat{x}=(x;1) x =(x;1),则 ω x + b \omega x+b ωx+b可以简写为 β T x ^ \beta^{T}\widehat{x} βTx 。再令 P 1 ( x ^ ; β ) = P ( y = 1 ∣ x ^ ; β ) P_{1}(\widehat{x};\beta)=P(y=1|\widehat{x};\beta) P1(x ;β)=P(y=1∣x ;β), P 0 ( x ^ ; β ) = P ( y = 0 ∣ x ^ ; β ) = 1 − P 1 ( x ^ ; β ) P_{0}(\widehat{x};\beta)=P(y=0|\widehat{x};\beta)=1-P_{1}(\widehat{x};\beta) P0(x ;β)=P(y=0∣x ;β)=1−P1(x ;β),将其代入到似然函数中:
P ( y i ∣ x i ; ω , b ) = y i P 1 ( x ^ i ; β ) + ( 1 − y i ) P 0 ( x ^ i ; β ) P(y_{i}|x_{i};\omega,b)=y_{i}P_{1}(\widehat{x}_{i};\beta)+(1-y_{i})P_{0}(\widehat{x}_{i};\beta) P(yi∣xi;ω,b)=yiP1(x i;β)+(1−yi)P0(x i;β)
这种表达形式是非常聪明的,一个通式可以表达出y取1和0两种情况。将之前推导出的后验概率代入到其中就可有如下推导:
P ( y i ∣ x i ; ω , b ) = y i e z 1 + e z + ( 1 − y i ) 1 1 + e z P(y_{i}|x_{i};\omega,b)=y_{i}\frac{e^{z}}{1+e^{z}}+(1-y_{i})\frac{1}{1+e^{z}} P(yi∣xi;ω,b)=yi1+ezez+(1−yi)1+ez1
上面的式子是我们需要最大化的式子,我们可以取倒数等价出一个最小化的式子:
P ( y i ∣ x i ; ω , b ) = y i 1 + e z e z + ( 1 − y i ) ( 1 + e z ) P(y_{i}|x_{i};\omega,b)=y_{i}\frac{1+e^{z}}{e^{z}}+(1-y_{i})(1+e^{z}) P(yi∣xi;ω,b)=yiez1+ez+(1−yi)(1+ez)
我们可以等价为每个样本属于真是标记的概率的倒数的总和最小,这样就变成了一个最优化问题。
将其代入到似然函数中取对数就可以得到:
l ( β ) = ∑ i = 1 m ( − y i β T x ^ i + l n ( 1 + e β T x ^ i ) ) l(\beta)=\sum_{i=1}^{m}(-y_{i}\beta^{T}\widehat{x}_{i}+ln(1+e^{\beta^{T}\widehat{x}_{i}})) l(β)=i=1∑m(−yiβTx i+ln(1+eβTx i))
上面这个式子便是我们最重要寻优的式子,也是逻辑回归模型的损失函数,我们可以利用最优化方法去寻得其最优解。逻辑回归的损失函数是关于 β \beta β 的高阶可导连续凸函数,根据凸优化理论,经典的数值优化方法例如梯度下降法、牛顿法等都可求得最优解,于是可以得到:
β ∗ = a r g m i n β l ( β ) \beta^{*}=\underset{\beta}{argmin} l(\beta) β∗=βargminl(β)
寻优的过程便是模型训练的过程。
逻辑回归sklearn参数总结
import sklearn.linear_model.LogisticRegression
参数:
**penalty **: str, ‘l1’ or ‘l2’, default: ‘l2’ ——正则化项
dual : bool, default: False ——对偶方程。默认是false。如果是true,则表示使用‘Dual formulation’,这种情况仅仅适合于penalty='l2’且solver用的是liblinear的情况;只要样本数大于特征数值,最好将dual=false
tol : float, default: 1e-4 ——迭代优化停止的条件
C : float, default: 1.0 ——正则化的强度,必须是正浮点数,数值越小正则化在损失函数中占的比重越大。
fit_intercept : bool, default: True 决定偏置b是否存在
ntercept_scaling : float, default 1. ——一个浮点数,只有当 solver=‘liblinear’ 才有意义。当采用 fit_intercept 时,相当于人造一个特征出来,该特征恒为 1,其权重为b 。在计算正则化项的时候,该人造特征也被考虑了。因此为了降低人造特征的影响,需要提供 intercept_scaling。(其实我也不知道怎么用)
class_weight : dict or ‘balanced’, default: None ——类别的权重。
如果为字典:则字典给出了每个分类的权重。
如果为字符串 ‘balanced’:则每个分类的权重与该分类在样品中出现的频率成反比。
如果未指定,则每个分类的权重都为 1。
random_state : int, RandomState instance or None, optional, default: None ——打乱数据时候用的随机数生成器(我也不知道为什么要打乱)
如果为整数,则它指定了随机数生成器的种子。
如果为RandomState实例,则指定了随机数生成器。
如果为None,则使用默认的随机数生成器。
solver : {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’} ——优化求解方法
liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
max_iter : int, default: 100 ——最大迭代次数。当选择newton-cg, sag and lbfgs这三种算法时才能用。
multi_class : str, {‘ovr’, ‘multinomial’}, default: ‘ovr’ ——指定对于多分类问题的策略,可以为如下的值。
‘ovr’ :采用 one-vs-rest 策略。
‘multinomial’:直接采用多分类逻辑回归策略。
verbose : int, default: 0 ——用于开启/关闭迭代中间输出的日志。
warm_start : bool, default: False ——如果为True,那么使用前一次训练结果继续训练,否则从头开始训练。
n_jobs : int, default: 1 ——指定任务并行时的 CPU 数量。如果为 -1 则使用所有了用的 CPU。
属性:
coef_ : array, shape (1, n_features) or (n_classes, n_features)
特征的权重向量
intercept_ : array, shape (1,) or (n_classes,) ——偏置b的值
n_iter_ : array, shape (n_classes,) or (1, ) ——实际迭代次数
方法就不多介绍了,有需求的可以到官方网站看。
除此之外,对于逻辑回归的调参经验,推荐刘建平这篇博客。