Pytorch 循环神经网络 nn.RNN() nn.RNNCell() nn.Parameter()不同方法实现

RNN

网络结构

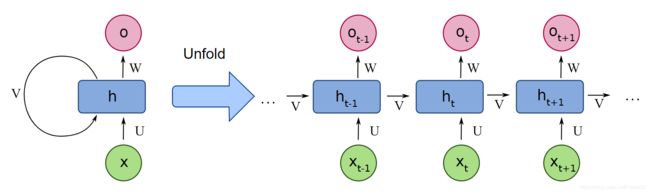
一个典型的单层RNN网络，结果如下所示。其实很简单就是一个神经元（蓝色模块），针对时序输入信号分别输入网络中，网络再每个时序进行输出，其中通过一个状态量记录时序信息。

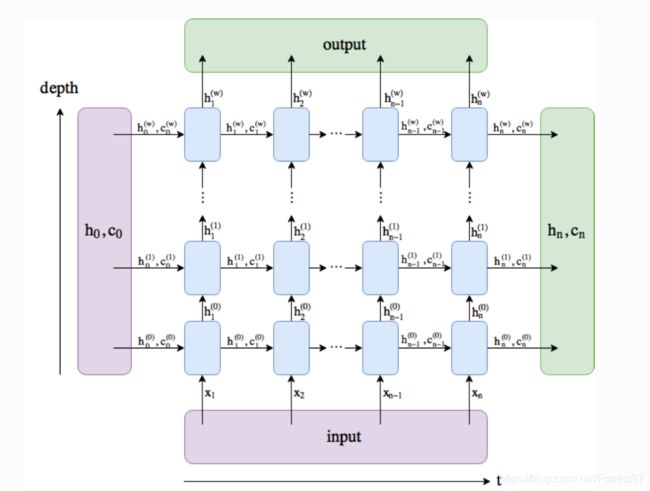
多层的RNN，上一次的输出ht是下一层的输入。

关键公式

RNN的关键特点隐层状态变量${\mathbf{H}}_t$，用于存储时序信息。
$${\mathbf{H}}_t=\varphi \left({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h\right)$$

$${\mathbf{O}}_t={\mathbf{H}}_t{\mathbf{W}}_{hq}+{\mathbf{b}}_q$$
多数网络会直接所有时序的$\mathbf{H}$作为输出

网络维度

输入数据$\mathbf{X}$维度表示[seq len, batch, h dim] =>[序列长度，batch, 序列的表示维度]=> [单词数， 句子数， 词维度]

刚开始接触RNNN会觉得这个输入形式有点怪，为什么batch维不是在0维度上。这里需要理解RNN的运算特点，RNN网络每次送入的数据${\mathbf{X}}_t$维度恰好就是[b, h dim]，循环送入seq len次。

${\mathbf{X}}_t$：维度[bath, h_dim]
${\mathbf{W}}_{xh}$：维度[h_dim, hidden_len]
${\mathbf{H}}_{t-1}$：维度[batch, hidden_len]
${\mathbf{W}}_{hh}$：维度[hidden_len, hidden_len]
${\mathbf{b}}_h$：维度[hidden_len]
${\mathbf{H}}_t$：维度[batch, hidden_len]
${\mathbf{W}}_{hq}$：维度[hidden_len, hidden_len]
${\mathbf{b}}_q$：维度[hidden_len]
${\mathbf{O}}_t$：维度[batch, hidden_len]

nn.RNN

构建一个 h_dim=10， hidden_len=20的2层RNN网络，同时我们打印出网络中的权重和偏差，以及shape

import  torch
from    torch import nn
from    torch.nn import functional as F

rnn = nn.RNN(input_size=10, hidden_size=20, num_layers=2)
print(rnn._parameters.keys())
print(rnn.weight_ih_l0.shape)
print(rnn.weight_hh_l0.shape)
print(rnn.bias_ih_l0.shape)
print(rnn.bias_hh_l0.shape)

odict_keys([‘weight_ih_l0’, ‘weight_hh_l0’, ‘bias_ih_l0’, ‘bias_hh_l0’, ‘weight_ih_l1’, ‘weight_hh_l1’, ‘bias_ih_l1’, ‘bias_hh_l1’])
torch.Size([20, 10])
torch.Size([20, 20])
torch.Size([20])
torch.Size([20])

可见Torch的RNN模型与表达式${\mathbf{H}}_t=\varphi \left({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h\right)$中的W和b完全对应，其中末尾的l0和l1表示layer层数编号。维度也刚好符合之前的推导。

对于nn.RNN的实例化对象rnn，输入包括输入input_tensor，以及初始h0（可省略，torch能根据网络参数和输入数据的shape添加）

# 可理解为一个字串长度为5， batch size为3， 字符维度为10的输入
input_tensor  = torch.randn(5, 3, 10)
# 两层RNN的初始H参数，维度[layers, batch, hidden_len]
h0 = torch.randn(2, 3, 20)

# output_tensor最后一层所有状态的输出， hn表示两层最后一个时序的状态输出
output_tensor, hn =rnn(input_tensor, h0)

print(output_tensor.shape, hn.shape)
print(output_tensor[-1][0], hn[-1][0])

torch.Size([5, 3, 20]) torch.Size([2, 3, 20])
tensor([-0.1818, 0.1286, -0.5069, -0.1739, -0.0189, -0.2936, 0.1807, -0.0592,
-0.4181, 0.0081, 0.4464, 0.0563, -0.6201, -0.6069, 0.3506, 0.3821,
0.0785, 0.3340, -0.2924, -0.0178], grad_fn=)
tensor([-0.1818, 0.1286, -0.5069, -0.1739, -0.0189, -0.2936, 0.1807, -0.0592,
-0.4181, 0.0081, 0.4464, 0.0563, -0.6201, -0.6069, 0.3506, 0.3821,
0.0785, 0.3340, -0.2924, -0.0178], grad_fn=)

可见input_tensor和output_tensor的shape相同，h0和hn的shape相同
且out_put_tensor的最后时序与hn的最后一层相同。

nn.RNNCell

也可以使用nn.RNNCell的API实现对多层的RNN网络每一层的Cell进行建模。

import  torch
from    torch import nn
from    torch.nn import functional as F

rnn = nn.RNN(input_size=10, hidden_size=20, num_layers=2)

input_tensor  = torch.randn(5, 3, 10)
h0 = torch.zeros(2, 3, 20)

output_tensor, hn =rnn(input_tensor, h0)

cell1 = nn.RNNCell(input_size=10, hidden_size=20)
# 多层的RNNCell input_size=hidden_len
cell2 = nn.RNNCell(input_size=20, hidden_size=20)
h1 = torch.zeros(3, 20)
h2 = torch.zeros(3, 20)
cell_out=[]
for xt in input_tensor:

    h1 = cell1(xt, h1)
    h2 = cell2(h1, h2)
    cell_out.append(h2)
    
print(hn.shape, h2.shape)
print(hn[-1][0], h2[0])

• 这里的发现相同的输入情况下，两种模型参数的输出不同，推测可能与网络初始化参数不同引起

GRU

门控循环单元（gated recurrent, GRU）引入了重置门（reset gate）和更新门（update gate）

网络结构

关键公式

重置门${\mathbf{R}}_t$和更新门${\mathbf{Z}}_t$计算
$$\begin{array}{l}{\mathbf{R}}_t=\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xr}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hr}+{\mathbf{b}}_r\right)\\ {\mathbf{Z}}_t=\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xz}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hz}+{\mathbf{b}}_z\right)\end{array}$$
候选隐藏状态${\tilde{\mathbf{H}}}_t$计算
$${\tilde{\mathbf{H}}}_t=\tanh \left({\mathbf{X}}_t{\mathbf{W}}_{xh}+\left({\mathbf{R}}_t\odot {\mathbf{H}}_{t-1}\right){\mathbf{W}}_{hh}+{\mathbf{b}}_h\right)$$

${\mathbf{X}}_t$是当前序列信息网络的唯一途径。当重置门${\mathbf{R}}_t$接近0，丢弃上一个时间的隐藏状态${\mathbf{H}}_{t-1}$，反之当重置门${\mathbf{R}}_t$接近1，保留上一个时间的隐藏状态${\mathbf{H}}_{t-1}$。重置门有助于捕捉时间序列里短期的依赖关系

隐藏状态${\mathbf{H}}_t$计算
$${\mathbf{H}}_t={\mathbf{Z}}_t\odot {\mathbf{H}}_{t-1}+\left(1-{\mathbf{Z}}_t\right)\odot {\tilde{\mathbf{H}}}_t$$

当更新门${\mathbf{Z}}_t$接近1，候选状态${\tilde{\mathbf{H}}}_t$无法传入更新隐藏状态${\mathbf{H}}_t$，即当${\mathbf{Z}}_t$接近1可以控制${\mathbf{H}}_t$更新，实现对较早隐藏状态的有效保持作用。更新门有助于捕捉时间序列里长期的依赖关系

网络维度

${\mathbf{X}}_t$：维度[bath, h_dim]
${\mathbf{W}}_{xr}$：维度[h_dim, hidden_len]
${\mathbf{W}}_{xz}$：维度[h_dim, hidden_len]
${\mathbf{W}}_{xh}$：维度[h_dim, hidden_len]
${\mathbf{H}}_{t-1}$：维度[batch, hidden_len]
${\mathbf{W}}_{hr}$：维度[hidden_len, hidden_len]
${\mathbf{W}}_{hz}$：维度[hidden_len, hidden_len]
${\mathbf{W}}_{hh}$：维度[hidden_len, hidden_len]
${\mathbf{H}}_t$：维度[batch, hidden_len]

nn.GRU

同样，构建一个 h_dim=10， hidden_len=20的2层RNN网络，同时我们打印出网络中的权重和偏差，以及shape

gru = nn.GRU(input_size=10, hidden_size=20, num_layers=2)
print(gru._parameters.keys())
print(gru.weight_ih_l0.shape)
print(gru.weight_hh_l0.shape)

odict_keys([‘weight_ih_l0’, ‘weight_hh_l0’, ‘bias_ih_l0’, ‘bias_hh_l0’, ‘weight_ih_l1’, ‘weight_hh_l1’, ‘bias_ih_l1’, ‘bias_hh_l1’])
torch.Size([60, 10])
torch.Size([60, 20])

这里我们可以看出网络的关键参数在网络中跟RNN的权重参数名相同只有weight_ih和weight_hh，但是在size上可以看出端倪。
weight_ih的维度恰好是${\mathbf{W}}_{xr}$，${\mathbf{W}}_{xz}$，${\mathbf{W}}_{xh}$在0维上的堆叠。

# 可理解为一个字串长度为5， batch size为3， 字符维度为10的输入
input_tensor  = torch.randn(5, 3, 10)
# 两层RNN的初始H参数，维度[layers, batch, hidden_len]
h0 = torch.randn(2, 3, 20)

# output_tensor最后一层所有状态的输出， hn表示两层最后一个时序的状态输出
output_tensor, hn =rnn(input_tensor, h0)

print(output_tensor.shape, hn.shape)
print(output_tensor[-1][0], hn[-1][0])

torch.Size([5, 3, 20]) torch.Size([2, 3, 20])
tensor([-0.4143, -0.1336, 0.0865, 0.0401, -0.3132, 0.3051, 0.0650, -0.1396,
-0.2653, -0.2919, 0.1540, -0.3338, 0.0277, -0.3881, 0.4366, -0.2255,
-0.0051, -0.0046, -0.1863, -0.2611], grad_fn=) tensor([-0.4143, -0.1336, 0.0865, 0.0401, -0.3132, 0.3051, 0.0650, -0.1396,
-0.2653, -0.2919, 0.1540, -0.3338, 0.0277, -0.3881, 0.4366, -0.2255,
-0.0051, -0.0046, -0.1863, -0.2611], grad_fn=)

网络的输出形式同RNN

nn.Parameter定义网络

跟进一步我们玩一个更底层，自己定义参数运算实现一个rnn函数

device = None
input_size, hidden_size = 10, 20
input_tensor  = torch.randn(5, 3, 10)
h0 = torch.zeros((3, 20), device=device)

def get_params():
    def _one(shape):
        ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
        return torch.nn.Parameter(ts, requires_grad=True)

    # 隐藏层参数
    W_xh = _one((input_size, hidden_size))
    W_hh = _one((hidden_size, hidden_size))
    b_h = torch.nn.Parameter(torch.zeros(hidden_size, device=device, requires_grad=True))
    # 输出层参数
    W_hq = _one((hidden_size, input_size))
    b_q = torch.nn.Parameter(torch.zeros(input_size, device=device, requires_grad=True))
    return nn.ParameterList([W_xh, W_hh, b_h, W_hq, b_q])


def rnn(inputs, state, params):
    # inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
    W_xh, W_hh, b_h, W_hq, b_q = params
    H = state
    outputs = []
    for X in inputs:
        H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
        Y = torch.matmul(H, W_hq) + b_q
        outputs.append(Y)
    return outputs, H


params = get_params()
outputs, state_new = rnn(input_tensor, h0, params)
print(len(outputs), outputs[0].shape, state_new[0].shape)

LSTM

网络结构

关键公式

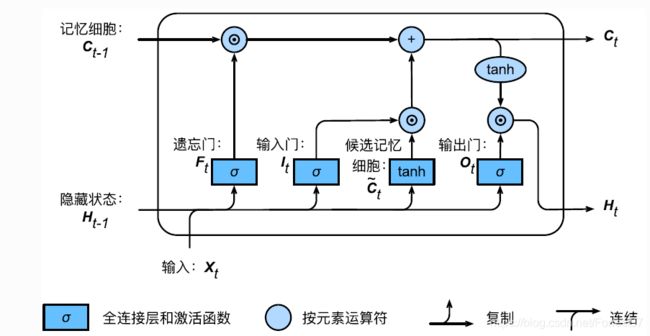
LSTM一共有三个门控单元，分别是: 输入门${\mathbf{I}}_t$，遗忘门${\mathbf{F}}_t$，输出门${\mathbf{O}}_t$，计算如下
$$\begin{array}{rl}{\mathbf{I}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xi}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hi}+{\mathbf{b}}_i\right)\\ {\mathbf{F}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xf}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hf}+{\mathbf{b}}_f\right)\\ {\mathbf{O}}_t& =\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xo}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{ho}+{\mathbf{b}}_o\right)\end{array}$$

跟GRU相似LSTM存在一个候选记忆状态${\tilde{\mathbf{C}}}_t$
$${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{X}}_t{\mathbf{W}}_{xc}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hc}+{\mathbf{b}}_c\right)$$

记忆状态${\mathbf{C}}_t$
$${\mathbf{C}}_t={\mathbf{F}}_t\odot {\mathbf{C}}_{t-1}+{\mathbf{I}}_t\odot {\tilde{\mathbf{C}}}_t$$

遗忘门用于控制上一步的记忆状态，输入门控制候选记忆状态。
当${\mathbf{F}}_t=1$，${\mathbf{I}}_t=0$时，新的信息无法进入，记忆状态将一直保存之前的的状态，因此很多人将遗忘门等于1定义为记忆门。

隐藏状态${\mathbf{H}}_t$
$${\mathbf{H}}_t={\mathbf{O}}_t\odot \tanh \left({\mathbf{C}}_t\right)$$

输出门${\mathbf{O}}_t$就更加直观了，负责记忆状态是否输出隐藏状态${\mathbf{H}}_t$

nn.LSTM

rnn = nn.LSTM(input_size=10, hidden_size=20, num_layers=2)
print(rnn._parameters.keys())
print(rnn.weight_ih_l0.shape)
print(rnn.weight_hh_l0.shape)

odict_keys([‘weight_ih_l0’, ‘weight_hh_l0’, ‘bias_ih_l0’, ‘bias_hh_l0’, ‘weight_ih_l1’, ‘weight_hh_l1’, ‘bias_ih_l1’, ‘bias_hh_l1’])
torch.Size([80, 10])
torch.Size([80, 20])

由于多了一个门控单元，0维度上又堆叠了一个hidden len
模型

input_tensor  = torch.randn(5, 3, 10)

output_tensor, hn =rnn(input_tensor)

代码参考
https://github.com/ShusenTang/Dive-into-DL-PyTorch