栈(二) -- 前缀、中缀、后缀表达式以及中缀转后缀简易计算器实现

前缀表达式(波兰式表达式)

1.1 前缀表达式的介绍

前缀表达式又称波兰式，前缀表达式的运算符位于操作数之前，如 (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6

1.2 前缀表达式的计算机求值

从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 和 次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果。
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:

1. 从右至左扫描，将6、5、4、3压入堆栈
2. 遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素），计算出3+4的值，得7，再将7入栈
3. 接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈
4. 最后是-运算符，计算出35-6的值，即29，由此得出最终结果

中缀表达式

2.1 中缀表达式的介绍

中缀表达式就是常见的运算表达式，即运算符位于操作数之间，如(3+4)×5-6。

2.2中缀表达式的计算机求值

中缀表达式的求值是我们人最熟悉的，但是对计算机来说却不好操作(前面栈(一) – 栈的基本介绍 的案例就能看的这个问题)，因此，在计算结果时，往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式.)

后缀表达式

3.1 中缀表达式的介绍

后缀表达式又称逆波兰表达式,与前缀表达式相似，只是运算符位于操作数之后， 如：(3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –

再比如

中缀表达式	后缀表达式(逆波兰表达式)
a+b	a b +
a+(b-c)	a b c - +
a+(b-c)*d	a b c - d * +
a+d*(b-c)	a d b c - * +
a=1+3	a 1 3 + =

3.2 后缀表达式的计算机求值

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:

1. 从左至右扫描，将3和4压入堆栈；
2. 遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
3. 将5入栈；
4. 接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
5. 将6入栈；
6. 最后是-运算符，计算出35-6的值，即29，由此得出最终结果

3.3 后缀表达式的计算机求值过程代码实现

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		// 为了方便逆波兰表达式的数字和符号使用空格隔开
		String suffixExpression = "4 5 * 8 - 60 + 8 2 / +";
		List rpnList = getListString(suffixExpression);
		System.out.println("rpnList=" + rpnList);
		int res = calculate(rpnList);
		System.out.println("计算的结果为：" + res);
	}

	// 依次将逆波兰表达式的数据和运算符放入到ArrayList中
	public static List getListString(String suffixExpression) {
		String[] split = suffixExpression.split(" ");
		List list = new ArrayList();
		for (String ele : split) {
			list.add(ele);
		}
		return list;
	}

	// * 1)从左至右扫描，将3和4压入堆栈；
	// * 2)遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
	// * 3)将5入栈；
	// * 4)接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
	// * 5)将6入栈；
	// * 6)最后是-运算符，计算出35-6的值，即29，由此得出最终结果
	// 完成对逆波兰表达式的计算
	public static int calculate(List ls) {
		// 创建栈
		Stack stack = new Stack();
		for (String item : ls) {
			if (item.matches("\\d+")) { // 匹配多位数
				// 入栈
				stack.push(item);
			} else {
				// pop出两个数，并运算，再入栈
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				switch (item) {
				case "+":
					res = num1 + num2;
					break;
				case "-":
					res = num1 - num2;
					break;
				case "*":
					res = num1 * num2;
					break;
				case "/":
					res = num1 / num2;
					break;
				default:
					throw new RuntimeException("运算结果有误");
				}
				// res 入栈
				stack.push("" + res);
			}
		}
		return Integer.parseInt(stack.pop());
	}

}

3.4 中缀表达式转换为后缀表达式

大家看到，后缀表达式适合计算式进行运算，但是人却不太容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将中缀表达式转成后缀表达式。

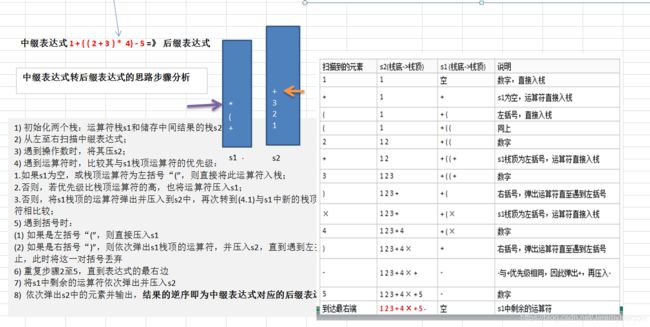
中缀表达式转后缀表达式的具体步骤：

1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2；
2. 从左至右扫描中缀表达式；
3. 遇到操作数时，将其压s2；
4. 遇到运算符时，比较其与s1栈顶运算符的优先级：
   (1) 如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
   (2) 否则，若优先级比栈顶运算符的高，也将运算符压入s1；
   (3) 否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；
5. 遇到括号时：
   (1) 如果是左括号“(”，则直接压入s1
   (2) 如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
6. 重复步骤2至5，直到表达式的最右边
7. 将s1中剩余的运算符依次弹出并压入s2
8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

举例说明:
将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程图解如下：

代码实现如下：
说明：因为s2这个栈在整个转化过程中，没有pop操作，并且最后需要逆序输出 这里不用Stack，直接使用ArrayList。

package com.mylove.stack;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class InfixExpressionToSuffix {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		// 完成将一个中缀表达式转成后缀表达式的功能
		// 1.1+((2+3)*4)-5 => 转成 1 2 3 + 4 * + 5 -
		// 2.因为直接对str进行操作不方便，因此先将 1+((2+3)*4)-5 中缀表达式转成对应的List 即 1+((2+3)*4)-5
		// => ArrayList[1，+，(，(，2，+，3，)，*，4，)，-，5]
		// 3.将得到的中缀表达式对应的List => 后缀表达式的List 即
		// ArrayList[1，+，(，(，2，+，3，)，*，4，)，-，5] => ArrayList[1，2，3，+，4，*，+，5，-]
		String expression = "1+((2+3)*4)-5";
		List infixExpressionList = toInfixExpressionList(expression);
		System.out.println("中缀表达式对应的List为：" + infixExpressionList);
		List suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
		System.out.println("后缀表达式对应的List为：" + suffixExpressionList);
		System.out.printf("expression=%d", calculate(suffixExpressionList));
	}

	 ArrayList[1，+，(，(，2，+，3，)，*，4，)，-，5] => ArrayList[1，2，3，+，4，*，+，5，-]
	public static List parseSuffixExpressionList(List ls) {
		// 定义两个栈
		Stack s1 = new Stack();// 符号栈
		List s2 = new ArrayList();// 存储中间结果
		// 遍历ls
		for (String item : ls) {
			if (item.matches("\\d+")) {
				s2.add(item);
			} else if (item.equals("(")) {
				s1.push(item);
			} else if (item.equals(")")) {
				// 如果是右括号")",则依次弹出s1栈顶的运算符，并压入s2,直到遇到左括号为止，这时将这一括号丢弃
				while (!s1.peek().equals("(")) {
					s2.add(s1.pop());
				}
				s1.pop();// 将s1栈中的左括号丢弃
			} else {
				// 当item的优先级小于等于s1栈顶运算符，将s1栈顶的运算符弹出并加入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较
				while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
					s2.add(s1.pop());
				}
				// item运算符优先级比栈顶运算符优先级高
				s1.push(item);
			}
		}
		// 将s1中剩余的运算符依次弹出并加入到s2中
		while (s1.size() != 0) {
			s2.add(s1.pop());
		}
		return s2;
	}

	// 将中缀表达式转换成对应的List
	public static List toInfixExpressionList(String s) {
		List ls = new ArrayList();
		int i = 0; // 指针用于遍历中缀表达式
		String str; // 对多位数的拼接
		char c; // 每遍历到一个字符就放到c中
		do {
			if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) { // 符号直接加入ls
				ls.add("" + c);
				i++;
			} else { // 如果是数字需要考虑多位数
				str = "";
				while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
					str += c;
					i++;
				}
				ls.add(str);
			}
		} while (i < s.length());
		return ls;
	}

	// * 1)从左至右扫描，将3和4压入堆栈；
	// * 2)遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
	// * 3)将5入栈；
	// * 4)接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
	// * 5)将6入栈；
	// * 6)最后是-运算符，计算出35-6的值，即29，由此得出最终结果
	// 完成对逆波兰表达式的计算
	public static int calculate(List ls) {
		// 创建栈
		Stack stack = new Stack();
		for (String item : ls) {
			if (item.matches("\\d+")) { // 匹配多位数
				// 入栈
				stack.push(item);
			} else {
				// pop出两个数，并运算，再入栈
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				switch (item) {
				case "+":
					res = num1 + num2;
					break;
				case "-":
					res = num1 - num2;
					break;
				case "*":
					res = num1 * num2;
					break;
				case "/":
					res = num1 / num2;
					break;
				default:
					throw new RuntimeException("运算结果有误");
				}
				// res 入栈
				stack.push("" + res);
			}
		}
		return Integer.parseInt(stack.pop());
	}
}

// 编写一个类Opertion 可以返回一个运算符对应的优先级
class Operation {
	private static int ADD = 1;
	private static int SUB = 1;
	private static int MUL = 2;
	private static int DIV = 2;

	// 写一个方法，返回对应的优先级数字
	public static int getValue(String opertion) {
		int result = 0;
		switch (opertion) {
		case "+":
			result = ADD;
			break;
		case "-":
			result = SUB;
			break;
		case "*":
			result = MUL;
			break;
		case "/":
			result = DIV;
			break;
		default:
			System.out.println("不存在该运算符");
			break;
		}
		return result;
	}
}

运行结果如下：