逻辑回归(四)—— 非线性逻辑回归
逻辑回归
说明
其实和线性的逻辑回归一模一样,还是以前的套路,把非线性的项看成单独的一个特征,多加几列就行了。
# 多项式特征处理
poly_reg = PolynomialFeatures(degree=3)
x_poly = poly_reg.fit_transform(x_data)
这样就行了,degree代表你要最高次是几次。
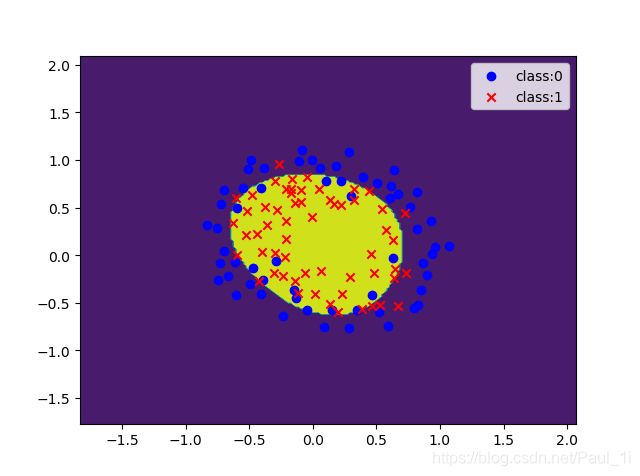
因为不再是直线,画图不好画,我们可以用等高线来画,总共只有两个高度:0或1。
测试数据是平面上的所有点,对于不同的高度(预测y值)画上不同的颜色即可,这样可以较为清楚地展示分类边界。
# 获得数据的范围
x_min,x_max = x_data[:,0].min()-1,x_data[:,0].max()+1
y_min,y_max = x_data[:,1].min()-1,x_data[:,1].max()+1
# 生成网格矩阵
xx,yy= np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02))
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(),yy.ravel()]).dot(np.array(ws)))
for i in range(len(z)):
if z[i]>0.5:
z[i]=1
else:
z[i]=0
z = z.reshape(xx.shape)
# 画等高线图
cs=plt.contourf(xx,yy,z)
plt.show()
其他和线性好像也没啥不一样了。
非线性逻辑回归
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report# 用于计算一些指标
from sklearn.preprocessing.data import PolynomialFeatures
# 这个函数用来画出类别不同的点
def showDots():
x0=[]
x1=[]
y0=[]
y1=[]
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i,0])
y0.append(x_data[i,1])
else:
x1.append(x_data[i,0])
y1.append(x_data[i,1])
# 画出点
scatter0 = plt.scatter(x0,y0,c='b',marker='o')
scatter1 = plt.scatter(x1,y1,c='r',marker='x')
# 画出图例说明
plt.legend(handles=[scatter0,scatter1],labels=['class:0','class:1'])
# 读文件
data = np.genfromtxt('../data/LR-testSet2.txt',delimiter=',')
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]
# 定义多项式回归
poly_reg = PolynomialFeatures(degree=3)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
# sigmoid函数
def sigmoid(x):
return 1.0/(1+np.exp(-x))
# 代价函数
def cost(xMat,yMat,ws):
part1 = np.multiply(yMat,np.log(sigmoid(xMat*ws)))
part2 = np.multiply(1-yMat,np.log(1-sigmoid(xMat*ws)))
return np.sum(part1+part2) / -len(xMat)
# 梯度下降法
def gradAscent(xArray,yArray):
xMat = np.mat(xArray)
yMat = np.mat(yArray)
lr = 0.003
epochs = 50000
costList = []
# 获得数据条数和特征数目
m,n = np.shape(xMat)
# 初始化权值全为1
ws = np.mat(np.ones((n,1)))
# 开始迭代
for i in range(epochs+1):
h = sigmoid(xMat*ws)
ws_grad = xMat.T*(h-yMat)/m
ws = ws - lr*ws_grad
if i%50==0:
costList.append(cost(xMat, yMat, ws))
return ws,costList
# 训练模型
ws,costList = gradAscent(x_poly, y_data)
# 获得数据的范围
x_min,x_max = x_data[:,0].min()-1,x_data[:,0].max()+1
y_min,y_max = x_data[:,1].min()-1,x_data[:,1].max()+1
# 生成网格矩阵
xx,yy= np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02))
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(),yy.ravel()]).dot(np.array(ws)))
for i in range(len(z)):
if z[i]>0.5:
z[i]=1
else:
z[i]=0
z = z.reshape(xx.shape)
# 画等高线图
cs=plt.contourf(xx,yy,z)
showDots()
plt.show()
# 分类的函数
def predict(ws):
xMat = np.mat(x_poly)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]
prediction = predict(ws)
print(classification_report(y_data,prediction))
使用sklearn库实现非线性逻辑回归
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_gaussian_quantiles
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# 生成数据
x_data,y_data = make_gaussian_quantiles(n_samples=500,n_features=2,n_classes=2)
# 多项式特征处理
poly_reg = PolynomialFeatures(degree=3)
x_poly = poly_reg.fit_transform(x_data)
# 创建模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_poly,y_data)
# 获得数据的范围
x_min,x_max = x_data[:,0].min()-1,x_data[:,0].max()+1
y_min,y_max = x_data[:,1].min()-1,x_data[:,1].max()+1
# 生成网格矩阵
xx,yy= np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02))
z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(),yy.ravel()]))
z = z.reshape(xx.shape)
# 画等高线图
cs=plt.contourf(xx,yy,z)
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()