生成模型 VS. 判别模型 Logistic 回归 VS. Softmax 回归
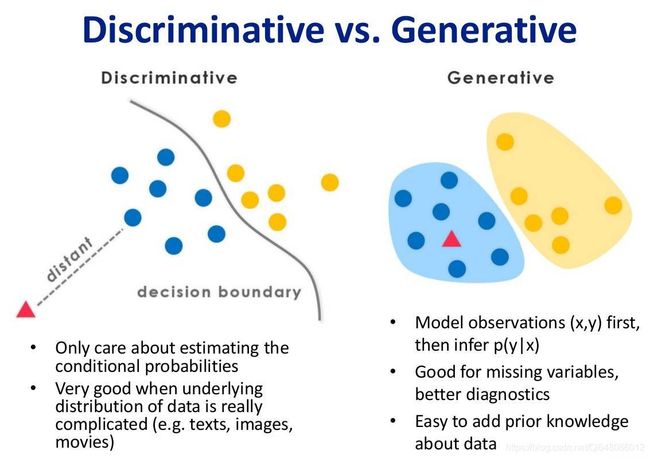
生成模型 VS. 判别模型
从概率分布的角度考虑,对于一堆样本数据,每个均有特征Xi对应分类标记yi。
生成模型:学习得到联合概率分布P(x,y),即特征x和标记y共同出现的概率,然后求条件概率分布。能够学习到数据生成的机制。
判别模型:学习得到条件概率分布P(y|x),即在特征x出现的情况下标记y出现的概率。
数据要求:生成模型需要的数据量比较大,能够较好地估计概率密度;而判别模型对数据样本量的要求没有那么多。
生成模型
在概率统计理论中, 生成模型是指能够随机生成观测数据的模型,尤其是在给定某些隐含参数的条件下。它给观测值和标注数据序列指定一个联合概率分布。在机器学习中,生成模型可以用来直接对数据建模(例如根据某个变量的概率密度函数进行数据采样),也可以用来建立变量间的条件概率分布。条件概率分布可以由生成模型根据贝叶斯定理形成。
生成模型的定义与判别模型相对应:生成模型是所有变量的全概率模型,而判别模型是在给定观测变量值前提下目标变量条件概率模型。因此生成模型能够用于模拟(即生成)模型中任意变量的分布情况,而判别模型只能根据观测变量得到目标变量的采样。判别模型不对观测变量的分布建模,因此它不能够表达观测变量与目标变量之间更复杂的关系。因此,生成模型更适用于无监督的任务,如分类和聚类。
典型的生成模型包括:
- 高斯混合模型和其他混合模型
- 隐马尔可夫模型
- 随机上下文无关文法
- 朴素贝叶斯分类器
- AODE分类器
- 潜在狄利克雷分配模型
- 受限玻尔兹曼机
如果观测数据是由生成模型中采样的,那么最大化数据似然概率是一个常见的方法。但是,大部分统计模型只是近似于真实分布,如果任务的目标是在已知一部分变量的值的条件下,对另一部分变量的推断,那么可以认为这种模型近似造成了一些对于当前任务来说不必要的假设。在这种情况下,使用判别模型对条件概率函数建模可能更准确,尽管具体的应用细节会最终决定哪种方法更为适用。
判别模型
在机器学习领域判别模型是一种对未知数据 $ {\displaystyle y} $与已知数据 x {\displaystyle x} x 之间关系进行建模的方法。判别模型是一种基于概率理论的方法。已知输入变量$ {\displaystyle x}$ ,判别模型通过构建条件概率分布 P ( y ∣ x ) {\displaystyle P(y|x)} P(y∣x)预测 y {\displaystyle y} y。
与生成模型不同,判别模型不考虑 x {\displaystyle x} x与 y {\displaystyle y} y 间的联合分布。对于诸如分类和回归问题,由于不考虑联合概率分布,采用判别模型可以取得更好的效果。而生成模型在刻画复杂学习任务中的依赖关系方面则较判别模型更加灵活。大部分判别模型本身是监督学习模型,不易扩展用于非监督学习过程。实践中,需根据应用的具体特性来选取判别模型或生成模型。
种类
- 逻辑回归
- 线性回归
- 支持向量机
- 提升方法
- 条件随机场
- 人工神经网络
- 随机森林
- 感知器
引入
监督学习的任务就是学习一个模型(或者得到一个目标函数),应用这一模型,对给定的输入预测相应的输出。这一模型的一般形式为一个决策函数Y=f(X),或者条件概率分布P(Y|X)。
监督学习方法又可以分为生成方法(generative approach)和判别方法(discriminative approach)。所学到的模型分别为生成模型(generative model)和判别模型(discriminative model)。
决策函数和条件概率分布
决策函数Y=f(X)
决策函数Y=f(X):你输入一个X,它就输出一个Y,这个Y与一个阈值比较,根据比较结果判定X属于哪个类别。例如两类(w1和w2)分类问题,如果Y大于阈值,X就属于类w1,如果小于阈值就属于类w2。这样就得到了该X对应的类别了。
条件概率分布P(Y|X)
你输入一个X,它通过比较它属于所有类的概率,然后输出概率最大的那个作为该X对应的类别。例如:如果P(w1|X)大于P(w2|X),那么我们就认为X是属于w1类的。
小结
两个模型都可以实现对给定的输入X预测相应的输出Y的功能。实际上通过条件概率分布P(Y|X)进行预测也是隐含着表达成决策函数Y=f(X)的形式的。
而同样,很神奇的一件事是,实际上决策函数Y=f(X)也是隐含着使用P(Y|X)的。因为一般决策函数Y=f(X)是通过学习算法使你的预测和训练数据之间的误差平方最小化,而贝叶斯告诉我们,虽然它没有显式的运用贝叶斯或者以某种形式计算概率,但它实际上也是在隐含的输出极大似然假设(MAP假设)。也就是说学习器的任务是在所有假设模型有相等的先验概率条件下,输出极大似然假设。
生成方法和生成模型
生成模型:无穷样本---->概率密度模型 =产生模型---->预测
生成方法由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y|X)=P(X,Y)/P(X)作为预测的模型。这样的方法之所以成为生成方法,是因为模型表示了给定输入X产生输出Y的生成关系。用于随机生成的观察值建模,特别是在给定某些隐藏参数情况下。典型的生成模型有:朴素贝叶斯法、马尔科夫模型、高斯混合模型。这种方法一般建立在统计学和Bayes理论的基础之上。
生成方法的特点
- 从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度;
- 生成方法还原出联合概率分布,而判别方法不能;
- 生成方法的学习收敛速度更快、即当样本容量增加的时候,学到的模型可以更快地收敛于真实模型;
- 当存在隐变量时,扔可以用生成方法学习,此时判别方法不能用
判别方法和判别模型
判别模型:有限样本---->判别函数 = 预测模型---->预测
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型。判别方法关心的是对给定的输入X,应该预测什么样的输出Y。典型的判别模型包括:k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、boosting方法和条件随机场等。判别模型利用正负例和分类标签,关注在判别模型的边缘分布。
判别方法的特点
- 判别方法寻找不同类别之间的最优分类面,反映的是异类数据之间的差异;
- 判别方法利用了训练数据的类别标识信息,直接学习的是条件概率P(Y|X)或者决策函数f(X),直接面对预测,往往学习的准确率更高;
- 由于直接学习条件概率P(Y|X)或者决策函数f(X),可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。
- 缺点是不能反映训练数据本身的特性
判别模型和生成模型对比
(1)训练时,二者优化准则不同
生成模型优化训练数据的联合分布概率;
判别模型优化训练数据的条件分布概率,判别模型与序列标记问题有较好的对应性。
(2)对于观察序列的处理不同
生成模型中,观察序列作为模型的一部分;
判别模型中,观察序列只作为条件,因此可以针对观察序列设计灵活的特征。
(3)训练复杂度不同
判别模型训练复杂度较高。
(4)是否支持无指导训练
生成模型支持无指导训练。
(5)本质区别
discriminative model 估计的是条件概率分布(conditional distribution)p(class|context)
generative model 估计的是联合概率分布(joint probability distribution)p()
另外,由生成模型可以得到判别模型,但由判别模型得不到生成模型。
对于跟踪算法
由于之前用Camshift方法做人脸的跟踪,这里看到了有关跟踪算法的说明,特此陈述一下。
跟踪算法一般来说可以分为两类:基于外观模型的生成模型或者基于外观模型的判别模型。
生成模型:一般是学习一个代表目标的模型,然后通过它去搜索图像区域,然后最小化重构误差。类似于生成模型描述一个目标,然后就是模式匹配了,在图像中找到和这个模型最匹配的区域,就是目标了。
判别模型:将跟踪问题看成一个二分类问题,然后找到目标和背景的决策边界。它不管目标是怎么描述的,那只要知道目标和背景的差别在哪,然后你给一个图像,它看它处于边界的那一边,就归为哪一类。
定义
监督学习的任务就是学习一个模型,应用这一模型,对给定的输入预测相应的输出,这个模型的一般形式为决策函数:
Y = f ( X ) Y=f(X) Y=f(X)
或者条件概率分布:
P ( Y ∣ X ) P(Y|X) P(Y∣X)
监督学习方法又可以分为生成方法(generative approach) 和判别方法(discriminative approach). 所学到的模型分别称为生成模型(generative model) 和判别模型(discriminative model).
—— 李航《统计学习方法》
同样地,在李航老师的这本《统计学习方法》中,对生成方法和判别方法做出了如下定义:
生成方法由数据学习联合概率分布 P ( X , Y ) P(X, Y) P(X,Y),然后求出条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)作为预测的模型,即生成模型:
P ( Y ∣ X ) = P ( X , Y ) P ( X ) P(Y|X)= \frac{P(X,Y)}{P(X)} P(Y∣X)=P(X)P(X,Y)
这样的方法之所以称为生成方法,是因为模型表示了给定输入 X 产生输出 Y 的生成关系,典型的生成模型有:朴素贝叶斯法和隐马尔可夫模型.
判别方法由数据直接学习决策函数 f ( X ) f(X) f(X)或者条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)作为预测的模型,即判别模型. 判别模型关心的是给定输入X,应当输出什么样的Y .典型的判别模型包括:k近邻法、感知机、决策树、逻辑斯谛回归模型、最大熵模型、支持向量机、提升方法和条件随机场等.
特点对比
优点
- 能计算出联合概率分布 P ( X , Y ) P(X,Y) P(X,Y),可以反映同类数据本身的相似度.
- 学习收敛速度更快,即当样本容量增加的时候,学习到的模型可以更快地收敛于真实模型.
- 能够用于数据不完整的情况,且能检测异常值.
缺点
- 含有更多的信息,但同样也需要更多的计算资源.
- 仅用于分类任务时,有许多冗余信息.
判别模型(discriminative model)
优点
- 学习的是条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) 或决策函数 f ( X ) f(X) f(X),直接面对预测问题,往往准确率更高.
- 可以对数据进行各种程度上的抽象、定义特征并使用特征,简化学习问题.
- 对分类任务,冗余信息更少,能节省计算资源.
缺点
- 不能反映数据本身的特性.
- 数据缺失或者异常值对预测结果的影响较大.
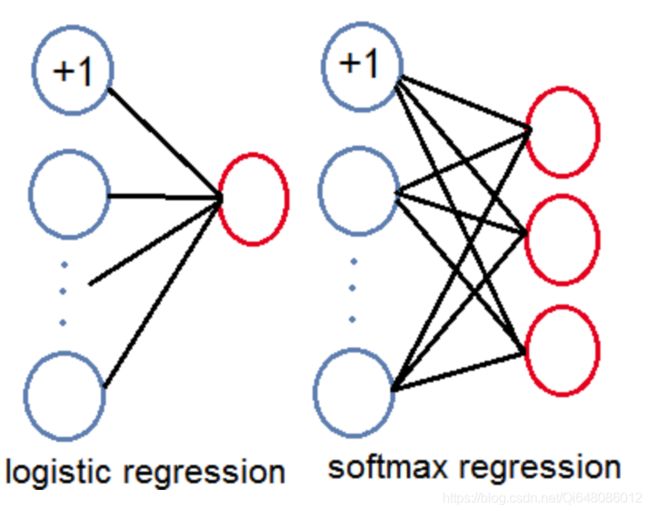
Logistic 回归 VS. Softmax 回归
其实 Softmax 就是 Logistic 的推广,Logistic 一般用于二分类,而softmax 是多分类。
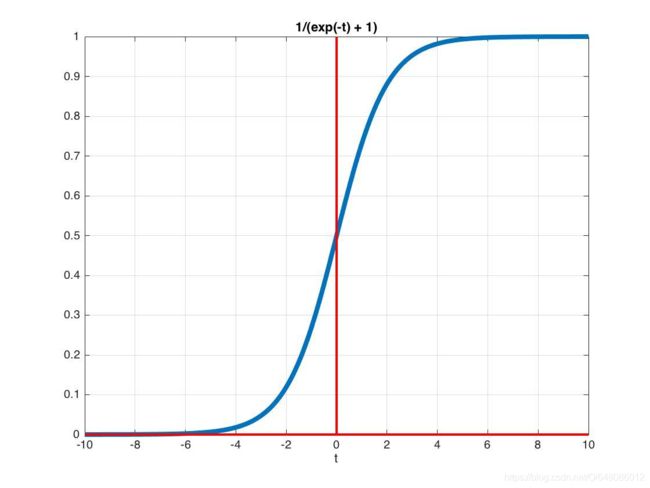
逻辑回归的激活函数是 sigmoid 函数,可理解成一个被 sigmoid 函数归一化后的线性回归,sigmoid 函数把实数映射到了 [0,1] 区间。当类别数 k = 2 时,SoftMax 回归退化为逻辑回归。
逻辑回归使用 sigmoid 函数。
逻辑回归
逻辑回归(Logistic regression)是一种对数几率模型(英语:Logit model,又译作逻辑模型、评定模型、分类评定模型)是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
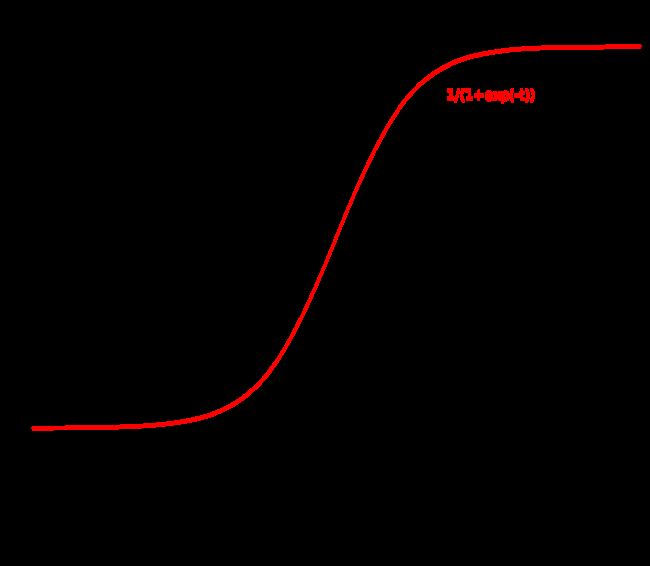
P ( Y = 1 ∣ X = x ) = e x ′ β 1 + e x ′ β P(Y=1|X=x)={\frac {e^{{x'\beta }}}{1+e^{{x'\beta }}}} P(Y=1∣X=x)=1+ex′βex′β
SoftMax 回归与多个 Logistic 回归二分类的区别
Logistic 回归可以通过推广到 SoftMax 回归来解决多分类问题。下面通过实例介绍 SoftMax 回归与多个 Logistic 回归二分类的区别。
使用 SoftMax 回归或者是多个 Logistic 回归二分类解决多分类问题,取决于类别之间是否互斥,例如,如果有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的 SoftMax 回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5)。
如果四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用 4 个二分类的 Logistic 回归分类器更为合适。这样,对于每个新的音乐作品 ,我们的算法可以分别判断它是否属于各个类别。
Logistic 回归以及 Softmax 回归与神经网络的关系
一般的神经网络有输入层,隐含层以及输出层构成,而上图中只有输入层和输出层,而没有隐含层。神经网络处理二分类时,输出层为一个节点,但处理K(K>2)分类问题时,数据节点为K个。值得注意的,在神经网络中的最后一层隐含层和输出层就可以看成是 Logistic 回归或 SoftMax 回归模型,之前的层只是从原始输入数据从学习特征,然后把学习得到的特征交给 Logistic 回归或 SoftMax 回归处理。
因此,可以把处理分类问题的神经网络分成两部分,特征学习和 Logistic 回归或 SoftMax 回归。