对于CNN卷积神经网络的前向传播和反向传播的理解
对于CNN卷积神经网络的前向传播和反向传播的理解
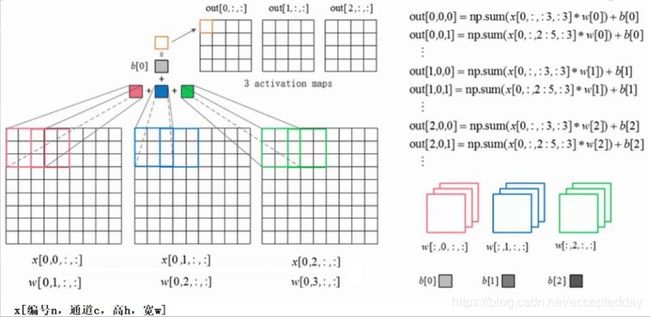
前向传播示意图:
咋一看这张图,作为初学者可能会不知所云( ̄ω ̄=)?但是想要很好的理解前向传播的原理,我们得从这张图细说。
文章目录
- 对于CNN卷积神经网络的前向传播和反向传播的理解
- 1.首先我们从x,w的参数组成说起?
- 2.filter滤波器与图片的对应关系是什么?
- 3.共享权重和偏重机制
- 4.反向传播的式子怎么得来的?
1.首先我们从x,w的参数组成说起?
如图左下角所示,x[编号n,通道c,高h,宽w],这里需要的注意的是通道c和编号n的作用。如图,这里输入的图片格式采用3通道,即R,G,B可以看作是输入图片的深度为3。
![]()
这里的0,1,2分别代表R,G,B三种颜色层,而w[…,0/1/2,…,…]也是同理。而编号n的作用在于识别是否为同一张照片,即如图,x[0,0,…],x[0,1,…],x[0,2,…]代表他们同属于某一张图片,采用编号0。
2.filter滤波器与图片的对应关系是什么?

接着,我们思考右上角的计算式?对于不断变换的h,w对应是什么意思呢?结合上图,我们发现是filter滤波器窗口w在x上不断的移动的结果,而h,c对应的位置发生了变化(即滤波器窗口在向右移动)。
而上述计算式中的out[编号n,x,y]中x,y对应的是最终输出的out中的坐标。
3.共享权重和偏重机制
还是上述的计算式,对于同一张图(R/G/B,而不是RGB三张图共享),采用共享filter滤波器权重w和偏重b。
当filter窗口扫描完一张图的所有像素位置,得到最终输出的out。这里需要的注意的是,滤波器的个数取决于上一层输入图的深度,即通道数。
换一种角度理解就是,输入图有多少层,便需要多少个filter滤波器去提取特征。
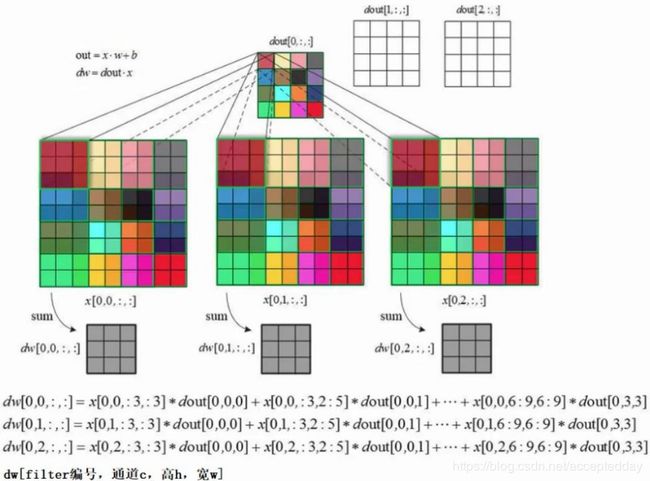
反向传播示意图:
4.反向传播的式子怎么得来的?
前向传播的关系式为:out=x*w+b,而反向传播时则需求解出dw是什么?
反向传播的目的:更新参数w。因此要先算出dw。假设上一层会传过来一个梯度dj/dout(j对out的求导),根据链式求导法则,因此dw = dj/dout * dout/dw =dj/dout * x ,在计算机中方便为变量命名的缘故,将dj/dout记为dout,dj/dw记为dw,即图中的情况。
即dw=dout*x;将dout反向乘以x得到dw。