环境感知与规划专题(六)——模型预测控制(MPC)在运动规划中的应用(二)
前言
上一篇中简述了模型预测控制在多旋翼飞行器运动规划中的应用。
本篇将针对采用线性MPC的多旋翼飞行器的运动规划方案进行详细推导。
系统模型的离散化
对于多旋翼飞行器这类三阶积分器模型,我们可以很容易得到其连续时间系统模型:
p ˙ = v v ˙ = a a ˙ = j \dot p=v\\[2ex] \dot v=a\\[2ex] \dot a=j\\[2ex] p˙=vv˙=aa˙=j
对其离散化,可得离散时间系统模型:
p i + 1 = p i + v i d t + 1 2 a i d t 2 + 1 6 j i d t 3 v i + 1 = v i + a i d t + 1 2 j i d t 2 a i + 1 = a i + j i d t i = [ 0 , 1 , 2... , K ] p_{i+1}=p_{i}+v_{i}dt+\frac{1}{2}a_{i}dt^{2}+\frac{1}{6}j_{i}dt^{3}\\[2ex] v_{i+1}=v_{i}+a_{i}dt+\frac{1}{2}j_{i}dt^{2}\\[2ex] a_{i+1}=a_{i}+j_{i}dt\\[2ex] i=[0,1,2...,K] pi+1=pi+vidt+21aidt2+61jidt3vi+1=vi+aidt+21jidt2ai+1=ai+jidti=[0,1,2...,K]
在得到离散时间系统模型之后,我们将其进行参数化,得到预测模型:
P = T p J + B p V = T v J + B v A = T a J + B a P = [ p 1 , p 2 , . . . , p K ] T V = [ v 1 , v 2 , . . . , v K ] T A = [ a 1 a 2 , . . . , a K ] T J = [ j 1 , j 2 , . . . , j K ] T P=T_{p}J+B_{p}\\[2ex] V=T_{v}J+B_{v}\\[2ex] A=T_{a}J+B_{a}\\[2ex] P=[p_{1},p_{2},...,p_{K}]^{T}\\[2ex] V=[v_{1},v_{2},...,v_{K}]^{T}\\[2ex] A=[a_{1}a_{2},...,a_{K}]^{T}\\[2ex] J=[j_{1},j_{2},...,j_{K}]^{T} P=TpJ+BpV=TvJ+BvA=TaJ+BaP=[p1,p2,...,pK]TV=[v1,v2,...,vK]TA=[a1a2,...,aK]TJ=[j1,j2,...,jK]T
预测模型参数的计算
在每一个预测周期,我们首先需要计算预测模型的相关参数,Matlab代码如下:
function [Tp, Tv, Ta, Bp, Bv, Ba] = getPredictionMatrix(K, dt, p_0, v_0, a_0)
Ta = zeros(K);
Tv = zeros(K);
Tp = zeros(K);
for i = 1 : K
Ta(i, 1:i) = ones(1, i) * dt;
end
for i = 1 : K
for j = 1 : i
Tv(i, j) = (i - j + 0.5) * dt ^ 2;
end
end
for i = 1 : K
for j = 1 : i
Tp(i, j) = ((i - j + 1) * (i - j) / 2 + 1 /6) * dt ^ 3;
end
end
Ba = ones(K, 1) * a_0;
Bv = ones(K, 1) * v_0;
Bp = ones(K, 1) * p_0;
for i = 1 : K
Bv(i) = Bv(i) + i * dt * a_0;
Bp(i) = Bp(i) + i * dt * v_0 + i ^ 2 / 2 * a_0 * dt ^ 2;
end
end
二次规划问题(QP)的求解
在已知预测模型的前提下,我们需要针对我们的规划目标设计对应的代价函数。
这里以设定终点速度为指定值,终点加速度为0,终点位置不做约束的情况作为案例,其他情况可自行推导。
我们设计如下代价函数:
min J w 1 ( V t − V ) T ( V t − V ) + w 2 A T A + w 3 J T J \min_{J}{w_{1}(V_{t}-V)^T(V_t-V)+w_{2}A^TA+w_{3}J^TJ}\\ Jminw1(Vt−V)T(Vt−V)+w2ATA+w3JTJ
将预测模型代入上式,可得:
min J J T ( w 1 T v T T v + w 2 T a T T a + w 3 I ) J + 2 ( w 1 ( B v − V t ) T T p + w 2 B a T T a ) J + c o n s t a n t \min_{J}{J^T(w_1{T_{v}^TT_{v}+w_{2}T_{a}^TT_{a}+w_{3}I})J+2(w_{1}(B_{v}-V_{t})^TT_{p}+w_{2}B_{a}^TT_{a})J+constant} JminJT(w1TvTTv+w2TaTTa+w3I)J+2(w1(Bv−Vt)TTp+w2BaTTa)J+constant
以上代价函数可转化为典型的二次规划问题:
H T x H + F T x H^TxH+F^Tx\\ HTxH+FTx
这里我们优化的变量为 J J J 。下一步,我们需要确定二次规划问题的约束条件。
硬约束与软约束
硬约束与软约束均能够界定优化问题的边界条件,以 A x ≤ b Ax\leq b Ax≤b 的形式表述。
以多旋翼飞行器的运动规划为例,由于飞行器存在明确的动力学极限,即有限的速度、加速度等状态参数,我们需要对规划的轨迹设定对应的约束条件。
硬约束界定了一个不可逾越的边界条件,运动规划的结果将严格遵守此边界条件。
T v J ≤ V m a x − B v − T v J ≤ V m a x + B v T a J ≤ A m a x − B a − T a J ≤ V m a x + B a T_{v}J\leq V_{max}-B_{v}\\[2ex] -T_{v}J\leq V_{max}+B_{v}\\[2ex] T_{a}J\leq A_{max}-B_{a}\\[2ex] -T_{a}J\leq V_{max}+B_{a} TvJ≤Vmax−Bv−TvJ≤Vmax+BvTaJ≤Amax−Ba−TaJ≤Vmax+Ba
由此可得对应的边界参数:
H = blkdiag(w2 * eye(K) + w1 * (Tv' * Tv) + w2 * (Ta' * Ta));
F = w1 * (Bv - v_t)' * Tv + w2 * Ba' * Ta;
A = [Tv; -Tv; Ta; -Ta];
b = [v_max * ones(K,1) - Bv; v_max * ones(K,1) + Bv; a_max *ones(K,1) - Ba; a_max * ones(K,1) + Ba];
J = quadprog(H, F, A, b);
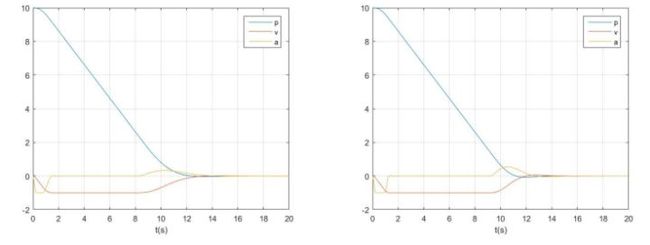
通过调节不同的权重值,能够改变不同的规划结果,可根据实际情况调整:
软约束则通过扩展优化变量、修改代价函数的方式进行优化问题的求解,适用于初始状态超过边界条件的情况。
例如,多旋翼飞行器的最大速度为3 m / s m/s m/s,而初始速度为5 m / s m/s m/s ,若采用硬约束,则二次规划问题无解,此时,需要通过软约束的方式解决该问题。
软约束的实质是在原本的代价函数的基础上,扩展一个惩罚函数 S ( L ) S(L) S(L) ,由此得到新的代价函数:
min J , L w 1 ( V t − V ) T ( V t − V ) + w 2 A T A + w 3 J T J + w 4 L T L \min_{J,L}{w_{1}(V_{t}-V)^T(V_t-V)+w_{2}A^TA+w_{3}J^TJ+w_{4}L^TL}\\ J,Lminw1(Vt−V)T(Vt−V)+w2ATA+w3JTJ+w4LTL
其约束条件则变为:
T v J ≤ V m a x − B v − L − T v J ≤ V m a x + B v + L T a J ≤ A m a x − B a − L − T a J ≤ V m a x + B a + L − L ≤ 0 T_{v}J\leq V_{max}-B_{v}-L\\[2ex] -T_{v}J\leq V_{max}+B_{v}+L\\[2ex] T_{a}J\leq A_{max}-B_{a}-L\\[2ex] -T_{a}J\leq V_{max}+B_{a}+L\\[2ex] -L\leq0 TvJ≤Vmax−Bv−L−TvJ≤Vmax+Bv+LTaJ≤Amax−Ba−L−TaJ≤Vmax+Ba+L−L≤0
由此可得对应的边界参数:
H = blkdiag(w3 * eye(K) + w1 * (Tv' * Tv) + w2 * (Ta' * Ta), w4 * eye(K));
F = [w1 * (Bv - v_t)' * Tv + w2 * Ba' * Ta zeros(1,K)];
A = [Tv eye(K); -Tv -eye(K); Ta eye(K); -Ta -eye(K); zeros(size(Ta)) -eye(K)];
b = [v_max * ones(K,1) - Bv; v_max * ones(K,1) + Bv; a_max * ones(K,1) - Ba; a_max * ones(K,1) + Ba; zeros(K,1)];
J = quadprog(H, F, A, b);
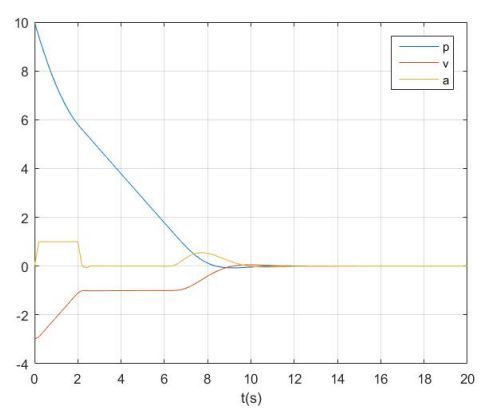
对于初始状态在上下界之外的情况,软约束能够使得规划之后的状态首先收敛于上下界范围内,然后再进行常规的二次规划问题求解,如下图:
施加软约束的二次规划结果不一定会严格遵守其边界条件,具体的优化结果取决于其扩展变量的权重。
运动规划后的控制算法框架
经过运动规划生成的轨迹,我们需要一个良好的控制器去跟踪,这里以多旋翼飞行器为例:
参考轨迹的位置设定值作为位置控制器的输入;
速度设定值加上位置控制器的输出(即速度前馈补偿量)作为速度控制器的输入;
加速度设定值加上速度控制器的输出(即加速度前馈补偿量)作为加速度控制器的输入;
加速度控制器的输出即为姿态控制器的输入;
通过内环控制器使得飞行器各状态量跟踪参考轨迹。
该控制框架即为上一篇中提到的Tube based MPC。
总结
本篇采用线性MPC算法对多旋翼飞行器的运动规划问题进行求解。
模型预测控制可用于手动操作飞行器时生成满足运动学约束的参考轨迹,也可以用于航点飞行时,生成参考轨迹。
- 对于手动操作模式
我们往往将遥控杆量映射为期望速度,即MPC运动规划问题中的终止速度。
通过MPC进行滚动优化,从而得到理想的参考轨迹,即本文通篇推导的代价函数所解决的问题。
- 对于自动航点模式
我们往往将航点位置、速度等信息直接作为终止状态,通过MPC进行滚动优化,得到理想参考轨迹。
本篇尚未对障碍物进行详解。由于障碍物约束往往是非凸的,无法用常规的QP算子进行解算,相对较为复杂。因此,将在后续的文章中单独进行详解。
作者简介: 一个被Coding耽误的无人机算法工程师,控制、导航略懂一二,热衷技术,喜欢乒乓、音乐、电影,欢迎交流。
知乎: @遥远的乌托邦
GitHub: https://github.com/DistantUtopia