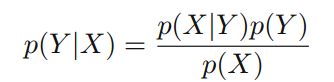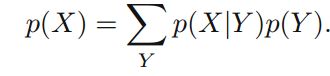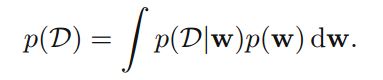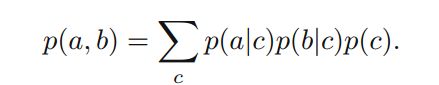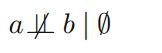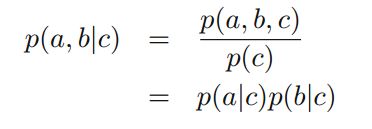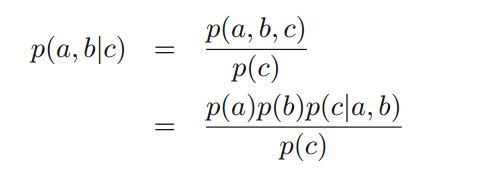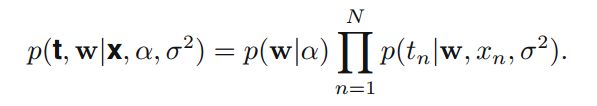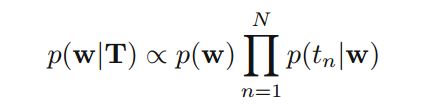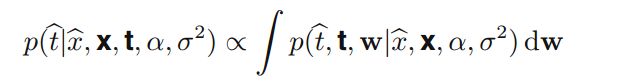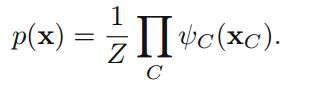1. 概率论
1.1 概念
对现实世界的不确定性进行建模
1.2概率计算的方法
- 加法规则
- 乘积规则
1.4 贝叶斯公式
通过上面的加法规则和乘法规则,以及P(X,Y)=P(Y,X)。我们可以得到贝叶斯公式:
其中P(X)为:
贝叶斯公式写成另外的一种常见的符号形式:
其中D表示观察到的数据,也成为Evidence, w表示相应的参数。
p(D|w)表示似然函数(likehood function)。P(w)成为参数w的先验。p(w|D)表示参数w的后验概率。
所以可以得到:
其中
1.3 相关的知识点
- 期望(本质是求平均)
MAP(点估计)与贝叶斯方法(核心是求期望)的不同 - 方差
- 微积分
2 概率论与图模型的关系
- 图模型和相对应的概率的对应关系。
2.1为什么需要图模型
优点:
- 以简单的方式将概率模型的结构可视化, 可以用于设计新模型
- 通过观察模型,更容易观察条件独立的性质
- 高级的一些推断和学习过程可以根据图计算表达。 (比如说因子图)
3.图模型
一般的网络图。
概率图中:节点表示随机变量,边表示因果关系或者依赖关系
3.1图模型的分类
图模型分为三类。
- 有向图或者贝叶斯网络
- 无向图或者马尔科夫随机场
- 因子图
3.2贝叶斯网络
常用于描述变量之间的因果关系
贝叶斯网络中的联合概率:
p(x)=P(xk|parent)
3.2.1例一
假设三个变量a,b,c上的联合概率分布p(a,b,c).
那么p(a,b,c)=p(c|ba)p(ba)=p(c|ba)p(b|a)p(a)
上面的图是全连接的。但是真实世界中变量之间确实是全连接的吗?
而且真正传递出概率分布性质的有趣信息是图中信息的缺失。
** 为什么呢?**
因为对于全连接的图模型可以用来代表所有的概率分布。这样的状态空间是巨大的。意义不大。
但是对于图中缺少边的模型,则只能对应于具有某些条件独立性质的
概率分布。
比如说:
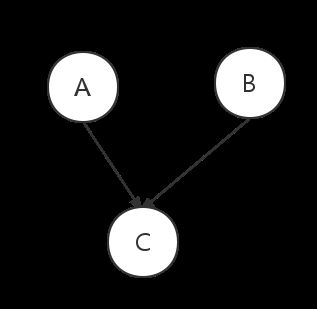
对于如下的图模型:
就只能够代表了A,B随机事件相互独立的情况。
那么从这个例子中我们可以看到:
非全链接的图模型中包含了相应的领域知识和因果关系。
3.2.2例二
对于下面一个关于学生成绩的例子。
我们假设各个随机变量出现的概率如下:
有了每个因子的分布之后, 就可以得到任意的概率分布了。方法就是:使用加法公式和乘积公式。
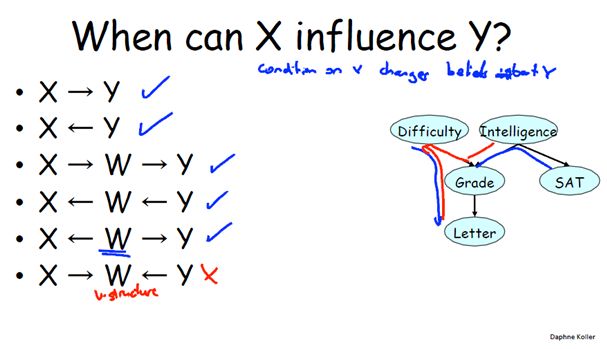
另外的一个问题是: 对于图模型中的变量怎么快速的知道它们之间是否相互影响。例如:
在左边对应的六种情况下,只有最后一种情况X→W←Y下X的概率不会影响到Y的概率。这是因为W不是被观察变量,其值是未知的,因此随机变量X的值不会影响随机变量Y的取值。有趣的是,当中间W变量成为被观察变量,上述结论就会发生变化。如下图所示
当WєZ时,即W为观察变量时,所有判断会变得相反。仍然以 X→W← Y 为例,此时W的值已知,比如已知某个学生Grade为B,那么此时学生的聪明程度Intelligence和课程难度Difficulty就不再条件独立了。比如,这种情况下如果课程比较容易,那边学生很聪明的概率较小;反之,若课程很难,则学生很聪明的概率较大。
结论: 概率影响的流动性反应了贝叶斯网络中随机变量条件独立性关系
那么贝叶斯网络中的独立性或者说影响的流动性是如何的呢?
3.2.3贝叶斯网络的独立性
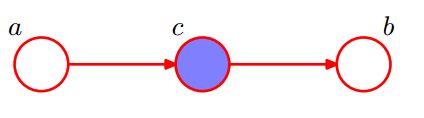
先来看看 ,图模型结构图中,三种常见的本地结构。
一般的如果没有观察变量,见结构1中的图,但是变量c是未知的。 那么:
对两边进行积分或者求和:
这个一般不能分解为p(a)p(b).因此:
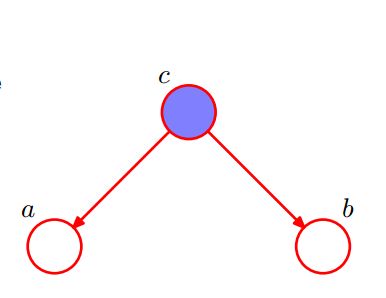
结构1:
因为:
所以可以得到:
我们称节点C关于路径 尾到尾tail-to-tail)
结构2:
可以得到:
所以同样可以得到A和B关于条件C独立。
我们称节点C关于 路径头到尾(head-to-tail)
结构3:
因为:
所以当C已知时得不到A与B相互独立。而对于当C为知时,A与B是相互独立的。
我们称C节点关于从A到B的路径 从头到头(head-to-head)
3.2.4 独立性总结
考虑一个一般的有向图,其中A,B,C是任意无交集的集合。我们的目的在于希望从图中迅速的观察到在给定C的情况下A与B是否相互独立。考虑A中任意节点到B中任意节点的所有可能路径,如果路径中包含一个满足下面任何一条的节点,那么就认为该路径是被阻隔的。
- 路径上的箭头以头到尾 或者尾到尾的方式交汇于这个节点。且这个节点在集合C中。
- 箭头以头到头的方式交汇于这个节点,且这个节点以及它的后继都不在C中。
如果所有的路径都被阻隔。那么我们说C把A和B隔开(d-划分),也就是有:
马尔科夫毯:
我们以马尔科夫毯来结束对贝叶斯网络独立性的讨论。考虑如下的图模型:
考虑变量x(i)对应节点上的条件概率分布,其中条件为所有剩余的变量。使用分解性质,可得:
最后与x(i)无关的变量可以提取,进行消除。唯一剩下的因子包括:p(xi|pai)以及p(Xk|Pak)其中xi为xk的父节点。
p(Xk|Pak)不仅仅依赖于xi,还依赖于xk的父节点。
我们可以将马尔科夫毯想象成为将xi与图中剩余部分隔离开的最小集合。
例三
(用于引出贝叶斯概率图模型中的表示)
考虑一个多项式回归的问题:
其中参数w为多项式稀疏,a为超参,t为观测变量。x为输入,另外一个为高斯分布的方差。
概率图模型为了清晰的在图形中表明各种的变量的状态。引入了特殊的表示法:包括观察变量,隐含变量,输入,参数,以及plate的概念。
其他的参考模型:LDA, PLSA模型图。
有了t,我们可以计算w的后验概率:
最终目标是对输入变量进行预测,假设给定一个输入值x^,我们需要预测输出。概率模型图如下:
那么模型的联合分布为:
对w进行积分就可以得到相应的预测值:
3.2.5 生成式模型
图模型描述了生成观测数据的生成式模型。因此这种模型通常被称为生成式模型。
对于概率模型的实际应用,通常情况下是,数量众多的变量对应于图的终端节点,较少的对应隐变量(hidden variables)。隐变量的主要作用是使得观测变量上的复杂分布可以表示为由简单条件分布构建的模型。(具体的原因,在E-M算法部分进行说明)
3.3 马尔科夫随机场
一个马尔科夫随机场也成为马尔科夫网络,或者无向图模型,包含了一组节点,每个节点都对应一个变量或者一组变量。链接是无向的,即不含箭头。
3.3.1 马尔科夫随机场的条件独立性
无向图的连接没有了方向,所以父子节点之间的对称性也消除了。所以可以使用一下两种方法判断是否独立:
- 考虑连接集合A与集合B的节点的所有的路径,如果所有这些路径到通过了集合C中的一个或者多个节点,那么所有这样的路径都被阻隔。因此条件独立存在。否则的话,条件独立的性质不一定成立。或者说一定有某个对应于该图的概率分布不满足条件独立的性质。
- 移除C中所有的节点,以及与这些节点相连的边。然后考察是否存在一条从A中任意节点到B中任意节点的路径。如果没有这样的路径,那么条件独立一定存在。
一个马尔科夫随机场的例子:
无向图的马尔科夫毯非常简单,因为节点只依赖于相邻的节点,而z给定邻居节点的情况下,条件独立于任何其他的节点。
3.3.2 分解性质
剩下的一个问题是:如何写出马尔科夫随机场的联合分布。也就是如何对联合分布进行 分解。
先来考虑图中的一个概念clique:
维基百科中的解释:a clique is a subset of vertices of an [undirected graph] such that its [induced subgraph]is [complete]; that is, every two distinct vertices in the clique are adjacent 。
马尔科夫随机场的联合概率可以分解为图中最大团快的势函数(potential functions )的乘积形式:
其中Z被称为划分函数,是一个归一化常数,等于:
我们假定势函数是大于0的,因此可以将势函数表示为指数的形式:
其中E(Xc)称为能量函数。
3.4因子图
因子图主要用于模型的推断过程。
参考文献:
书籍《Pattern Recognition andMachine Learning》 第八章