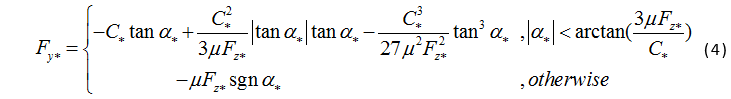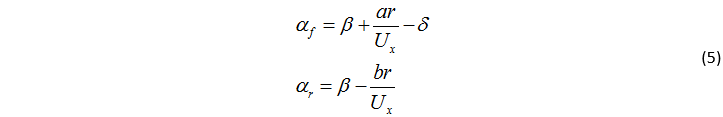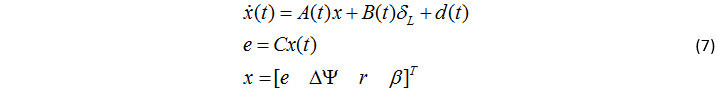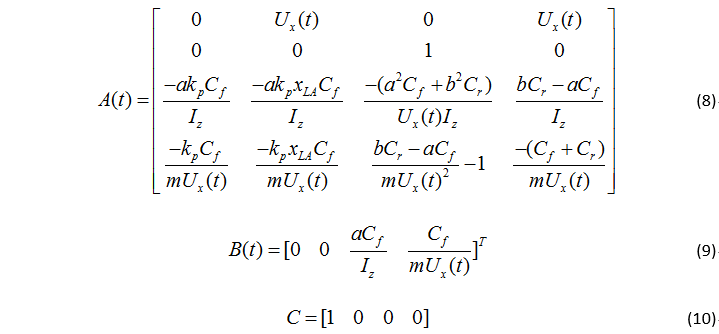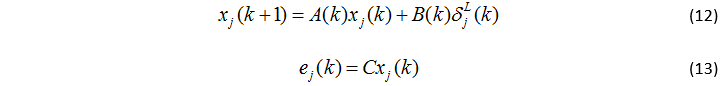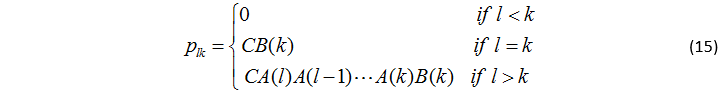迭代学习控制算法在自动驾驶车辆轨迹跟踪中的应用
本文由同济智能汽车研究所编译,转载请注明出处。文章译自2015年美国控制年会的会议论文《Path Tracking of Highly Dynamic Autonomous Vehicle Trajectories via Iterative Learning Contro》
本文由同济智能汽车研究所编译,转载请注明出处。
文章译自2015年美国控制年会的会议论文
《Path Tracking of Highly Dynamic Autonomous Vehicle Trajectories via Iterative Learning Control》
原作者:Nitin R. Kapania and J. Christian Gerdes
编者按:随着自动驾驶控制的发展,越来越多的人工智能或者机器学习的算法被应用在智能汽车底盘动力学控制器设计当中。由于实际车辆动力学系统的复杂性,控制器设计过程中往往忽略了系统的高阶动态以及非线性特性,导致车辆跟踪性能的降低。而智能算法恰恰能够补偿车辆动力学特性的变化,在一定程度上提高自动驾驶性能。文章通过一个简单的转角控制例子,验证了迭代学习算法在自动驾驶运动控制中的应用,值得借鉴。
摘要:自动驾驶车辆能够通过激进的驾驶操作在极限条件下尽可能地利用轮胎与路面间的附着能力,从而保持车辆的行驶能力。然而,在附着极限的条件下,车辆动力学的高度非线性和建模难度使控制器设计变得更加困难。其中,一种提高车辆的参考路径跟踪性能的可行办法是通过重复相同的操作,利用迭代学习控制(ILC)算法确定合适的瞬态转向控制输入参数。为探究这一概念的可能性,文章将学习算法应用在自动驾驶赛车的路径跟踪中。对ILC而言,赛车是一种理想的应用场景。因为赛车会在附着极限下沿着同一赛道反复行驶,从而产生多组可复现的非线性车辆动力学数据。仿真结果被用于设计和验证PD和二次最优迭代学习控制算法的收敛性,而奥迪TTS赛车在加州雷山赛道的试验结果也将在下文中展现。结果表明,这两种算法都可以修正路径跟踪的瞬态误差,并显著提高参考前馈控制器的性能。
1、前言
随着感知技术和线控技术的发展,相较于传统人类驾驶员,自动驾驶车辆能够在紧急情况下对车辆进行合理干预,从而提高安全性。类似的情况包括紧急避障[1]和由于驾驶员的误操作引起的车辆打滑[2]。而在极限条件下驾驶操作的最大难点在于路径跟踪过程中车辆的附着条件和转向响应呈现高度非线性。并且,一些难以测量的干扰(如路面倾角、坡度、局部附着系数突变…)对车辆的瞬态响应都有很大影响[3]。
ILC是一种确定复杂路径跟踪转向控制参数的有效方法。迭代学习已经成功应用于多种循环控制过程当中。通过利用以往的误差信息,ILC逐渐确定合适的控制输入,从而使得系统输出能够准确跟踪参考轨迹。最新的研究已经将ILC应用于路面自动驾驶车辆和飞行器中。Chen[4]在2006年提出了一种简单的ILC算法来提高全轮转向车辆的路径跟踪能力。2013年,Sun提出了一种ILC方法来保证高速列车的速度稳定性。同时,Purwin也在无人机控制中设计了一种利用最小二乘方法的ILC控制器。
本文在自动驾驶赛车的特定场景中实现迭代转向控制算法的应用。由于赛车在相同的赛道上循环行驶,并且行驶工况都迫近路面附着极限,赛车成为自动驾驶初期迭代学习控制的理想对象和场景。因为每一圈赛道的参考路径曲率都保持不变,系统的未知扰动和车辆的动力学特性被认为是可复现的,并且可以用ILC算法进行补偿。然而,值得一提的是,当车辆由于前轴轮胎力丧失而产生强烈的不足转向时,控制器不能有效控制车辆的行驶。在这种情况下,附加额外的转角对车辆的轨迹跟踪不会再有任何作用,因此,车辆的目标车速和转向曲率都需要进行修正。
文章架构如下:第二部分介绍了赛车跟踪参考路径时的平面线性模型。因为方向盘转角输入和车辆的路径跟踪误差之间的传递函数是开环不稳定的,所以需要在转向控制系统中加入一个车道保持的稳定性控制系统,而闭环的动力学系统将在所谓的“lifted-domain”中体现。第三部分提出了一个PD-ILC控制,并设计了一个低通滤波器来加速控制系统的收敛。利用“lifted-domain”的办法调整控制增益和小侧向的系统稳定性,而在大侧向工况下则利用非线性仿真预测期望的系统跟踪响应。第四部分提出了一个基于二次最优的Q-ILC控制器,可以准确地考虑车辆的速度变化。第五部分给出了在奥迪TTS试验平台车辆上加速度接近0.8g的时候两种控制器的试验数据。
2、车辆系统动力学和问题概述
本文中,自动驾驶车辆用最小时间沿着给定赛道行驶的控制目标分为侧向运动控制问题和纵向运动控制问题。侧向控制器利用方向盘转角输入跟踪参考轨迹(图1.a)。赛道一般以曲率沿着距离的变化表示(图1.b)。对于雷山赛道,可以利用文献[7]的办法计算最高速度和曲率的分布图。另外,车速跟踪控制器[8]不受ILC控制器的影响。
图 1.a Thunderhill Raceway
图 1.b 曲率与速度分布图
A.侧向车辆动力学
图2.a给出车辆跟踪给定曲率路径的示意图。车辆偏离期望路径的侧向位移误差e是ILC算法的测量输出。由于ILC控制器需要通过数次迭代来确定合适的前馈控制输入,因此,要求系统的控制输入和控制输出之间满足渐进稳定的关系。对于主动转向控制系统,转角和侧向位移误差的传递函数可以由原点处的两个极点表征,因此需要一个额外的反馈稳定性控制器。
图 2 二自由度平面车辆轨迹跟踪模型
本文利用预瞄控制作为系统的反馈稳定性控制器。预瞄误差定义为:
其中,△Ψ是车辆的航向角误差,XLA是预瞄距离,一般约5-20m。反馈控制律为:
![]()
kp为比例增益系数。控制律(2)是由一般的车道保持控制算法拓展得到的,文献[9]给出了kp和xLA的选择方法。文献[10]证明了在轮胎力饱和情况下该系统的稳定性。
通过增加反馈控制器,侧向位移误差的闭环动力学系统取决于三个状态:车辆侧偏角、横摆角速度以及航向角误差。车辆平面运动的系统动力学模型如下:
由于自动驾驶赛车常常行驶在轮胎的附着极限边缘,侧向力通过非线性的Fiala刷子轮胎模型进行建模,并假设附着系数不变以及轮胎力的抛物线假设[11]。前后轴的侧向力分别是前后轮胎侧偏角的函数,如式(4)所示。
线性轮胎侧偏角通过式(5)计算得到。
B.“lifted-domain”中的线性时变模型
虽然式(4)的非线性轮胎模型能够较好地反映极限工况下的轮胎力饱和现象,但是本文设计的两个ILC控制器需要一个线性系统假设。因此,在小侧向工况下,简单的线性轮胎模型如下:
线性时变模型考虑了车辆前进速度的变化。尽管式(3)中缺乏车辆的纵向动力学模型,考虑速度变化后能够让系统动力学控制更加精确。时变状态空间矩阵为:
假设每一圈的扰动都保持一致:
将系统离散化后得到:
k是时间采样下标,j是圈数。将系统动力学方程在“lifted-domain”中表示能够有利于ILC控制器的设计。
假设车速不变的话,我们将得到一个只有N个元素的线性时不变系统,因此P矩阵将会成为一个托普利兹矩阵。
3
控制器设计
在获得了上一圈的转向动态和完整的位移误差数据之后,下一步就是设计控制算法来确定下一圈的转角控制输入。如文献[12],采用常规的迭代学习算法框架来确定转角输入:
其中,Q是滤波矩阵,L是学习矩阵。在下一节中,Q和L矩阵将通过PD类型的ILC控制器和二次最优Q-ILC控制器得到。
A.比例-微分PD控制器
PD-ILC控制器通过前一圈的侧向位移误差和误差微分数据计算得到当前的转角输入:
通过式(16)得到学习矩阵L为:
在选择比例增益系数和微分增益系数的时候需要避免每一圈之间的瞬态响应变差,同时需要避免在最终收敛之前初期的路径跟踪误差快速增大。这是ILC控制器设计过程中的一般要求,可以通过满足一定的单调收敛条件[12]来保证。
其中,σ是最大特征值。如此,γ给出了每一圈路径跟踪误差变化的上限值。
图3中给出未经滤波PD控制器(Q=I)和经过一个2Hz低通滤波PD控制器的不同γ值。图中,γ的取值为kp和kd控制器参数的各等高线。低通滤波器通过排除微小跟踪误差引起的控制输入振荡来保证系统的单调稳定性。由于滤波是作用在下一圈的控制输入信号中,因此可以认为是零相位的。
图 3 控制器参数分布图
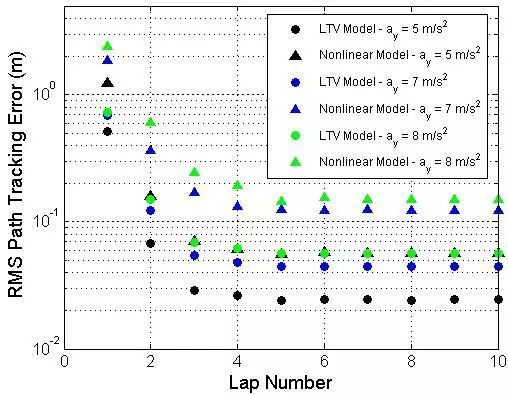
但是,测试系统的线性稳定性对于控制器的设计来说是不够的,因为赛车往往行驶在附着极限边缘,此时车辆的动力学特性为高度非线性的。为了测试PD控制器的可行性,利用图1 的曲率和速度图进行多圈的仿真来验证车辆的路径跟踪性能。图4给出了线性模型和非线性模型的路径跟踪误差的仿真结果均方根。结果表明,当车辆行驶至极限条件时,相比于期望的线性模型,ILC控制器的跟踪性能有一定程度的弱化,但仍然满足迭代收敛。
图 4 PD-ILC控制器仿真结果
B.二次最优控制器
另外一种方法是通过优化代价函数确定下一圈的转角控制输入:
其中,T、R、S分别是对应的权重矩阵。通过求解优化问题可以计算出期望的控制器和滤波参数矩阵[13]:
相较于PD控制器,二次最优控制器的优点在于能够考虑系统时变的动态P变化。这使得ILC控制器算法能够补偿由于车速变化引起的转向动力学特性变化。但是,这也将给每一圈计算Q和L矩阵的时候带来过大的运算负担。
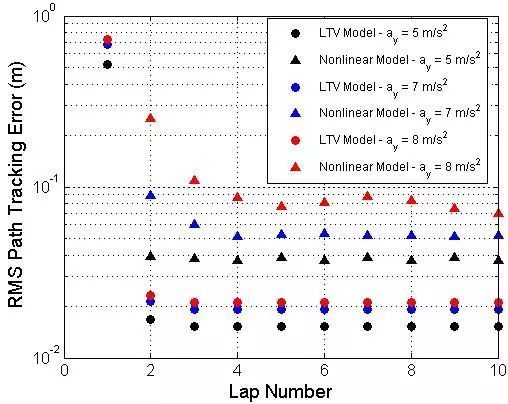
图5给出二次最优控制器的仿真结果,其中T=R=I,S=100I。为简化处理,选择单位矩阵作为权重矩阵的初始值,并根据反复试验进行调整。仿真结果与图4的结果类似,在非线性轮胎动力学特性部分,控制器的性能有一定的恶化。但是,仿真结果仍然证明了控制器能够保证侧向位移跟踪误差的快速收敛,在侧向加速度约0.8g的工况下,均方根误差约为8-9cm。
图 5 Q-ILC控制器仿真结果
4、试验结果
以上两种控制器均在加州雷山赛道上进行了实车试验验证,并采集了相关试验数据。试验平台车辆为奥迪TTS自动驾驶车辆,装备了EPS电机、主动制动器和线控电子油门(图6)。
图 6 试验平台
通过集成差分GPS系统和IMU传感器纪录车辆的状态信息,并利用定位算法计算车辆的侧向位移误差、航向角误差和行驶距离。转角控制器的更新频率为200Hz,数据采集频率为10Hz,每一圈的数据都用于计算迭代学习的转角控制输入。然后利用插值查表的方式沿着行驶距离更新控制器的参数。为了保证车辆的稳定性,利用基于稳态前馈转角控制算法[3]保证车辆的第一圈侧向位移误差不超过1m。
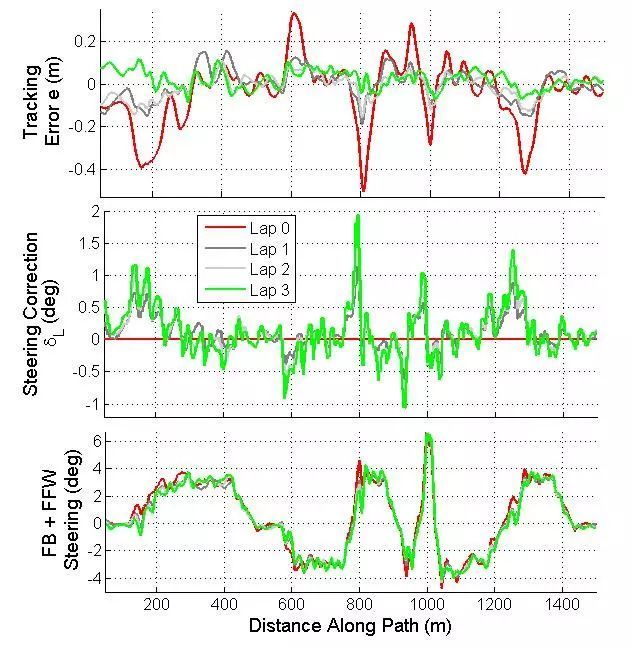
图7给出PD-ILC控制器的控制输入和跟踪误差。车辆的最大加速度为0.8g。在第一圈,尽管“前馈-反馈”控制器的采样频率很高,极限工况下轮胎的欠阻尼动力学特性仍然造成了跟踪误差的突变。但是,随着两三圈试验过后,迭代学习算法能够有效减小跟踪误差。Q-ILC控制器的表现与此类似。
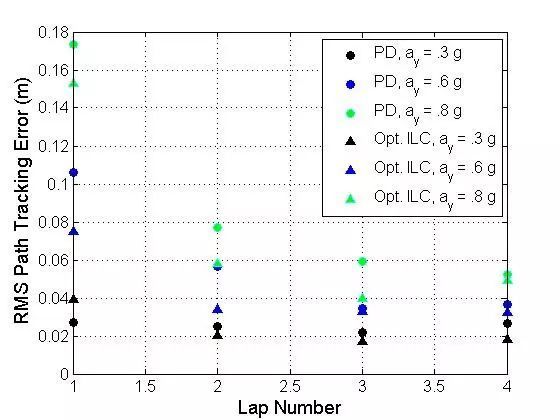
图8是跟踪不同加速度强度所需速度的结果。结果表明,在较小车辆加速度强度下,线性模型能够较为准确地表征车辆的动力学特性,“前馈-反馈”控制器能够很好地跟踪上期望的参考路径,因此,迭代学习算法的改善空间较小。但是,随着车速逐渐增加,轮胎的非线性特性增强,路径跟踪性能也受到影响,此时迭代学习算法能够有效地提高车辆的路径跟踪性能。实际结果表明,PD-ILC和Q-ILC的控制性能较为接近,而当测试进入结尾阶段,路径跟踪误差的均方根却有轻微的增加。仿真结果中并没有类似的现象,这可能是系统中每一圈未建模的传感器噪声和不同扰动造成的。通过调整增益矩阵中的参数应该可以抑制这一现象,或者可以考虑在车辆性能收敛后停止迭代学习算法。
图 7 PD-ILC控制器轨迹跟踪试验结果,峰值侧向加速度约为0.8g
图 8 两种控制器在不同加速度下的试验结果
5、结论
本文验证了迭代学习控制算法在自动驾驶赛车转角控制中的应用。两种迭代学习控制器PD-ILC和Q-ILC都经过了仿真和试验验证,可以有效减小由于车辆极限工况下侧向动力学高度非线性变化引起的侧向位移跟踪误差。两种控制器的性能表现接近,而PD-ILC方法的运算负担较轻,能够满足实时需求。虽然文章提出的控制器能够满足自动驾驶赛车在相同赛道上的路径跟踪需求,迭代学习算法在更多自动驾驶场景的应用仍需要更多的研究工作。
6、参考文献
[1] J. Funke and J. C. Gerdes, “Simpleclothoid paths for autonomous vehicle lane changes at the limits of handling,”in ASME 2013 Dynamic Systems and Control Conference. American Society ofMechanical Engineers, 2013, pp. V003T47A003–V003T47A003.
[2] V. Turri, A. Carvalho, H. Tseng, K. H.Johansson, and F. Borrelli, “Linear model predictive control for lane keeping and obstacleavoidance on low curvature roads,” 2013.
[3] N. R. Kapania and J. C. Gerdes, “Anautonomous lanekeeping system for vehicle path tracking and stability at thelimits of handling,” in 12th International Symposium on Advanced VehicleControl, 2014.
[4] Y. Q. Chen and K. L. Moore, “Apractical iterative learning pathfollowing control of an omni-directionalvehicle,” Asian Journal of Control, vol. 4, no. 1, pp. 90–98, 2002.
[5] H. Sun, Z. Hou, and D. Li, “Coordinatediterative learning control schemes for train trajectory tracking with overspeedprotection,” IEEE Trans. on Automation Science and Engineering, vol. 10, no. 2,pp. 323–333, 2013.
[6] O. Purwin and R. DAndrea, “Performingand extending aggressive maneuvers using iterative learning control,” Roboticsand Autonomous Systems, vol. 59, no. 1, pp. 1–11, 2011.
[7] P. A. Theodosis and J. C. Gerdes,“Generating a racing line for an autonomous racecar using professional drivingtechniques,” in Dynamic Systems and Control Conference, 2011, pp. 853–860.
[8] K. Kritayakirana, “Autonomous vehiclecontrol at the limits of handling,” Ph.D. dissertation, Stanford University,2012.
[9] E. J. Rossetter and J. C. Gerdes, “Astudy of lateral vehicle control under a virtual force framework,” in Proc.International Symposium on Advanced Vehicle Control, Hiroshima, Japan, 2002.
[10] K. L. Talvala and J. C. Gerdes,“Lanekeeping at the limits of handling: Stability via lyapunov functions and acomparison with stability control,” in Dynamic Systems and Control Conference,2008, pp. 361– 368.
[11] H. B. Pacejka, Tire and VehicleDynamics, 3rd ed. Butterworth-Heinemann, 2012.
[12] D. A. Bristow, M. Tharayil, and A. G.Alleyne, “A survey of iterative learning control,” Control Systems, IEEE, vol.26, no. 3, pp. 96–114, 2006.
[13] D. A. Bristow and B. Hencey, “A q,lfactorization of norm-optimal iterative learning control,” in 47th IEEEConference on Decision and Control, 2008. IEEE, 2008, pp. 2380–2384.