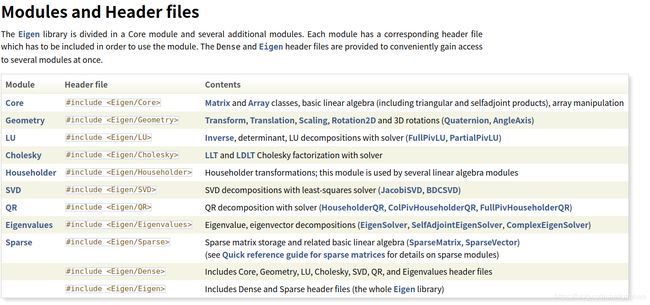
eigen库学习笔记
#简介
Eigen是有关线性代数(矩阵、向量等)的c++模板库。支持SSE2/3/4, ARM NEON (32-bit and 64-bit), PowerPC AltiVec/VSX (32-bit and 64-bit) instruction sets, S390x SIMD (ZVector)
简单的例子
#include matrices and vectors
eigen库是支持matrix和vector的相互运算的,并且也支持隐式的转换。官方提供了一个简单的例子:
#include matrix的进阶:The Matrix class
typedef
matrix具有六个template parameters:
Matrix
下面三个都是default,我们关注上三个。
- Scalar is the scalar type of the coefficients (e.g., float, double,
bool, int, etc.). - RowsAtCompileTime and ColsAtCompileTime are the
number of rows and columns of the matrix as known at compile-time or
Dynamic. - Options can be ColMajor or RowMajor, default is ColMajor.
(see class Matrix for more options)
任何的横纵向组合都是被允许的,比如:
Matrix // Dynamic number of columns (heap allocation)
Matrix // Dynamic number of rows (heap allocation)
Matrix // Fully dynamic, row major (heap allocation)
Matrix // Fully fixed (usually allocated on stack)
这是标准的写法,当然我们完全可以选择简写:
Matrices:
Matrix <=> MatrixXf
Matrix <=> VectorXd
Matrix <=> RowVectorXi
Matrix <=> Matrix3f
Matrix <=> Vector4f
Arrays:
Array <=> ArrayXXf
Array <=> ArrayXd
Array <=> RowArrayXi
Array <=> Array33f
Array <=> Array4f
两种写法是没区别的:
int main()
{
Matrix2d m;
m(0, 0) = 3;
m(1, 0) = 2.5;
m(0, 1) = -1;
m(1, 1) = m(1, 0) + m(0, 1);
std::cout << "Here is the matrix m:\n"
<< m << std::endl;
Matrix<double, 2, 2> m1;
m1(0, 0) = 3;
m1(1, 0) = 2.5;
m1(0, 1) = -1;
m1(1, 1) = m1(1, 0) + m1(0, 1);
std::cout << "Here is another matrix m1:\n"
<< m1 << std::endl;
}
Conversion between the matrix and array worlds:
int main()
{
Array22f a1, a2;
Matrix2f m1, m2;
m1 = a1 * a2; // coeffwise product, implicit conversion from array to matrix.
a1 = m1 * m2; // matrix product, implicit conversion from matrix to array.
a2 = a1 + m1.array(); // mixing array and matrix is forbidden
m2 = a1.matrix() + m1;
std::cout << m2 << std::endl;
std::cout << a2 << std::endl;
}
构造函数和初始化:
***Constructors:
Vector4d v4;
Vector2f v1(x, y);
Array3i v2(x, y, z);
Vector4d v3(x, y, z, w);
VectorXf v5; // empty object
ArrayXf v6(size);
Matrix4f m1;
MatrixXf m5; // empty object
MatrixXf m6(nb_rows, nb_columns);
***Comma initializer
Vector3f v1; v1 << x, y, z;
ArrayXf v2(4); v2 << 1, 2, 3, 4;
Matrix3f m1; m1 << 1, 2, 3,
4, 5, 6,
7, 8, 9;
***Comma initializer (bis)
int rows=5, cols=5;
MatrixXf m(rows,cols);
m << (Matrix3f() << 1, 2, 3, 4, 5, 6, 7, 8, 9).finished(),
MatrixXf::Zero(3,cols-3),
MatrixXf::Zero(rows-3,3),
MatrixXf::Identity(rows-3,cols-3);
cout << m;
resizing
int main()
{
MatrixXd m(3, 4);
m(0, 0) = 3;
m(1, 0) = 2.5;
m(0, 1) = -1;
m(1, 1) = m(1, 0) + m(0, 1);
cout << "m is \n"
<< m << endl;
m.resize(4, 3);
cout << "m1 is\n"
<< m << endl;
std::cout << "The matrix m is of size "
<< m.rows() << "x" << m.cols() << std::endl;
std::cout << "It has " << m.size() << " coefficients" << std::endl;
VectorXd v(2);
v.resize(5);
std::cout << "The vector v is of size " << v.size() << std::endl;
std::cout << "As a matrix, v is of size "
<< v.rows() << "x" << v.cols() << std::endl;
}
resize会把原来矩阵destroy,如果想要保持这些元素,可以使用conservativeResize()
storage orders
The entries of a matrix form a two-dimensional grid. However, when the matrix is stored in memory, the entries have to somehow be laid out linearly. There are two main ways to do this, by row and by column.
Matrix<int, 3, 4, ColMajor> Acolmajor;//ColMajor is not necessary here
Acolmajor << 8, 2, 2, 9,
9, 1, 4, 4,
3, 5, 4, 5;
cout << "The matrix A:" << endl;
cout << Acolmajor << endl << endl;
cout << "In memory (column-major):" << endl;
for (int i = 0; i < Acolmajor.size(); i++)
cout << *(Acolmajor.data() + i) << " ";
cout << endl << endl;
Matrix<int, 3, 4, RowMajor> Arowmajor = Acolmajor;
cout << "In memory (row-major):" << endl;
for (int i = 0; i < Arowmajor.size(); i++)
cout << *(Arowmajor.data() + i) << " ";//这里.data()指针指向矩阵的第一个元素
cout << endl;
output is:
The matrix A:
8 2 2 9
9 1 4 4
3 5 4 5
In memory (column-major):
8 9 3 2 1 5 2 4 4 9 4 5
In memory (row-major):
8 2 2 9 9 1 4 4 3 5 4 5
Map
对于原始的数据,可以使用Map复用原来的数据地址
int main()
{
float data[] = {1, 2, 3, 4};
Map<Vector3f> v1(data); // uses v1 as a Vector3f object
cout << "v1 is:" << v1 << endl;
cout << endl;
Map<ArrayXf> v2(data, 3); // uses v2 as a ArrayXf object
cout << "v2 is:" << v2 << endl;
cout << endl;
Map<Array22f> m1(data); // uses m1 as a Array22f object
cout << "m1 is:" << m1 << endl;
cout << endl;
Map<MatrixXf> m2(data, 2, 2); // uses m2 as a MatrixXf object
cout << "n2 is:" << m2 << endl;
cout << endl;
// float data[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
// Map> v1(data, 3); // = [1,3,5]
// Map> v2(data, 3, InnerStride<>(3)); // = [1,4,7]
// Map> m2(data, 2, 3); // both lines |1,4,7|
// Map> m1(data, 2, 3, OuterStride<>(3)); // are equal to: |2,5,8
}
aliasing
int main()
{
Matrix2d m = Matrix2d::Random();
cout << "Matrix2d m is: \n"
<< m << endl;
cout << endl;
Matrix2d m2;
m2 = m.transpose();
cout << "transpose is: \n"
<< m2 << endl;
cout << endl;
MatrixXd m3;
m3 = m * m2;
cout << "multiplication is: \n"
<< m3 << endl;
cout << endl;
double data[] = {1, 2, 3, 4};
Map<Matrix2d>v1(data);
cout << "v1 is \n"
<< v1 << endl;
}
output is:
Matrix2d m is:
0.680375 0.566198
-0.211234 0.59688
transpose is:
0.680375 -0.211234
0.566198 0.59688
multiplication is:
0.783491 0.194234
0.194234 0.400886
v1 is
1 3
2 4
矩阵的运算
int main()
{
MatrixXd m(4, 4);
m(0, 0) = 3;
m(1, 0) = 2.5;
m(0, 1) = -1;
m(1, 1) = m(1, 0) + m(0, 1);
int rowsize = m.rows();//查看矩阵的维度
int colsize = m.cols();
int SIZE = m.size();
cout << "row is:\n"
<< rowsize << endl;
cout << "col is:\n"
<< colsize << endl;
cout << "size is: \n"
<< SIZE << endl;
std::cout << m << std::endl;
MatrixXd m2 = Eigen::Matrix4d::Random();
m += m2;//基本的矩阵运算
std::cout << m << std::endl;
std::cout << std::endl;
m *= 2;
std::cout << m << std::endl;
std::cout << std::endl;
std::cout << -m << std::endl;
std::cout << std::endl;
//7. 求矩阵的转置、共轭矩阵、伴随矩阵
std::cout << m.transpose() << std::endl;
std::cout << std::endl;
std::cout << m.conjugate() << std::endl;
std::cout << std::endl;
std::cout << m.adjoint() << std::endl;
std::cout << std::endl;
m.transposeInPlace();
std::cout << m << std::endl;
std::cout << std::endl;
//8. 矩阵相乘、矩阵向量相乘
std::cout << m * m << std::endl;
std::cout << std::endl;
Eigen::Vector4d vec4d(1, 2, 3, 4);
std::cout << m * vec4d << std::endl;
std::cout << std::endl;
std::cout << vec4d.transpose() * m << std::endl;
std::cout << std::endl;
//9. 矩阵的块操作
std::cout << m << std::endl;
std::cout << std::endl;
MatrixXd block2;
block2 = m.block(1, 1, 2, 2);
std::cout << block2 << std::endl; matrix.block(i,j, p, q) :
//表示返回从矩阵(i, j)开始,每行取p个元素,每列取q个元素所组成的临时新矩阵对象,原矩阵的元素不变;
std::cout << std::endl;
std::cout << m.block<1, 2>(0, 0) << std::endl; //matrix.block(i, j) :为一个p行q列的子矩阵,
//该定义表示从原矩阵中第(i, j)开始,获取一个p行q列的子矩阵,返回该子矩阵组成的临时矩阵对象,原矩阵的元素不变;
std::cout << std::endl;
std::cout << m.col(1) << std::endl;
std::cout << std::endl;
std::cout << m.row(0) << std::endl;
std::cout << std::endl;
}
output is:
row is:
4
col is:
4
size is:
16
3 -1 0 0
2.5 1.5 0 0
0 0 0 0
0 0 0 0
3.68038 -0.176705 -0.444451 -0.270431
2.28877 0.895103 0.10794 0.0268018
0.566198 -0.329554 -0.0452059 0.904459
0.59688 0.536459 0.257742 0.83239
7.36075 -0.353411 -0.888901 -0.540862
4.57753 1.79021 0.21588 0.0536036
1.1324 -0.659109 -0.0904118 1.80892
1.19376 1.07292 0.515484 1.66478
-7.36075 0.353411 0.888901 0.540862
-4.57753 -1.79021 -0.21588 -0.0536036
-1.1324 0.659109 0.0904118 -1.80892
-1.19376 -1.07292 -0.515484 -1.66478
7.36075 4.57753 1.1324 1.19376
-0.353411 1.79021 -0.659109 1.07292
-0.888901 0.21588 -0.0904118 0.515484
-0.540862 0.0536036 1.80892 1.66478
7.36075 -0.353411 -0.888901 -0.540862
4.57753 1.79021 0.21588 0.0536036
1.1324 -0.659109 -0.0904118 1.80892
1.19376 1.07292 0.515484 1.66478
7.36075 4.57753 1.1324 1.19376
-0.353411 1.79021 -0.659109 1.07292
-0.888901 0.21588 -0.0904118 0.515484
-0.540862 0.0536036 1.80892 1.66478
7.36075 4.57753 1.1324 1.19376
-0.353411 1.79021 -0.659109 1.07292
-0.888901 0.21588 -0.0904118 0.515484
-0.540862 0.0536036 1.80892 1.66478
50.9107 42.1972 7.37523 16.2694
-3.22846 1.50231 0.420272 2.94527
-6.81771 -3.67439 -0.208235 -0.017952
-6.50846 -1.9001 2.2001 3.11581
24.688
5.54135
1.33356
11.6522
1.82378 9.02 6.77862 11.5452
7.36075 4.57753 1.1324 1.19376
-0.353411 1.79021 -0.659109 1.07292
-0.888901 0.21588 -0.0904118 0.515484
-0.540862 0.0536036 1.80892 1.66478
1.79021 -0.659109
0.21588 -0.0904118
7.36075 4.57753
4.57753
1.79021
0.21588
0.0536036
7.36075 4.57753 1.1324 1.19376
给出一些与matlab功能的对应写法
这部分来自matlab与eigen对比
#include
// 基本用法
// Eigen // Matlab // 注释
x.size() // length(x) // 向量的长度
C.rows() // size(C,1) // 矩阵的行数
C.cols() // size(C,2) // 矩阵的列数
x(i) // x(i+1) // 访问向量元素(Matlab的下标从1开始计数)
C(i,j) // C(i+1,j+1) // 访问矩阵元素
A << 1, 2, 3, // 初始化A,元素也可以是矩阵,先按列堆叠,再按行堆叠。
4, 5, 6,
7, 8, 9;
B << A, A, A; // B 是3个A水平排列
A.fill(10); // 将A的所有元素填充为10
// Eigen // Matlab 注释
MatrixXd::Identity(rows,cols) // eye(rows,cols) //单位矩阵
C.setIdentity(rows,cols) // C = eye(rows,cols) //单位矩阵
MatrixXd::Zero(rows,cols) // zeros(rows,cols) //全零矩阵
C.setZero(rows,cols) // C = zeros(rows,cols) //全零矩阵
MatrixXd::Ones(rows,cols) // ones(rows,cols) //全一矩阵
C.setOnes(rows,cols) // C = ones(rows,cols) //全一矩阵
MatrixXd::Random(rows,cols) // rand(rows,cols)*2-1 //MatrixXd::Random 返回范围为(-1, 1)的均匀分布的随机数
C.setRandom(rows,cols) // C = rand(rows,cols)*2-1 //返回范围为(-1, 1)的均匀分布的随机数
VectorXd::LinSpaced(size,low,high) // linspace(low,high,size)' //返回size个等差数列,第一个数为low,最后一个数为high
v.setLinSpaced(size,low,high) // v = linspace(low,high,size)' //返回size个等差数列,第一个数为low,最后一个数为high
VectorXi::LinSpaced(((hi-low)/step)+1, // low:step:hi //以step为步长的等差数列。((hi-low)/step)+1为个数
low,low+step*(size-1)) //
// Matrix 切片和块。下面列出的所有表达式都是可读/写的。
// 使用模板参数更快(如第2个)。注意:Matlab是的下标是从1开始的。
// Eigen // Matlab // 注释
x.head(n) // x(1:n) //前n个元素
x.head() // x(1:n) //前n个元素
x.tail(n) // x(end - n + 1: end) //倒数n个元素
x.tail() // x(end - n + 1: end) //倒数n个元素
x.segment(i, n) // x(i+1 : i+n) //切片
x.segment(i) // x(i+1 : i+n) //切片
P.block(i, j, rows, cols) // P(i+1 : i+rows, j+1 : j+cols) //块
P.block(i, j) // P(i+1 : i+rows, j+1 : j+cols) //块
P.row(i) // P(i+1, :) //第i行
P.col(j) // P(:, j+1) //第j列
P.leftCols() // P(:, 1:cols) //前cols列
P.leftCols(cols) // P(:, 1:cols) //前cols列
P.middleCols(j) // P(:, j+1:j+cols) //中间cols列
P.middleCols(j, cols) // P(:, j+1:j+cols) //中间cols列
P.rightCols() // P(:, end-cols+1:end) //后cols列
P.rightCols(cols) // P(:, end-cols+1:end) //后cols列
P.topRows() // P(1:rows, :) //前rows行
P.topRows(rows) // P(1:rows, :) //前rows行
P.middleRows(i) // P(i+1:i+rows, :) //中间rows行
P.middleRows(i, rows) // P(i+1:i+rows, :) //中间rows行
P.bottomRows() // P(end-rows+1:end, :) //最后rows行
P.bottomRows(rows) // P(end-rows+1:end, :) //最后rows行
P.topLeftCorner(rows, cols) // P(1:rows, 1:cols) //左上角块
P.topRightCorner(rows, cols) // P(1:rows, end-cols+1:end) //右上角块
P.bottomLeftCorner(rows, cols) // P(end-rows+1:end, 1:cols) //左下角块
P.bottomRightCorner(rows, cols) // P(end-rows+1:end, end-cols+1:end) //右下角块
P.topLeftCorner() // P(1:rows, 1:cols) //左上角块
P.topRightCorner() // P(1:rows, end-cols+1:end) //右上角块
P.bottomLeftCorner() // P(end-rows+1:end, 1:cols) //左下角块
P.bottomRightCorner() // P(end-rows+1:end, end-cols+1:end) //右下角块
// 特别说明:Eigen的交换函数进行了高度优化
// Eigen // Matlab
R.row(i) = P.col(j); // R(i, :) = P(:, j)
R.col(j1).swap(mat1.col(j2)); // R(:, [j1 j2]) = R(:, [j2, j1]) //交换列
// Views, transpose, etc;
// Eigen // Matlab
R.adjoint() // R' // 共轭转置
R.transpose() // R.' or conj(R') // 可读/写 转置
R.diagonal() // diag(R) // 可读/写 对角元素
x.asDiagonal() // diag(x) // 对角矩阵化
R.transpose().colwise().reverse() // rot90(R) // 可读/写 逆时针旋转90度
R.rowwise().reverse() // fliplr(R) // 水平翻转
R.colwise().reverse() // flipud(R) // 垂直翻转
R.replicate(i,j) // repmat(P,i,j) // 复制矩阵,垂直复制i个,水平复制j个
// 四则运算,和Matlab相同。但Matlab中不能使用*=这样的赋值运算符
// 矩阵 - 向量 矩阵 - 矩阵 矩阵 - 标量
y = M*x; R = P*Q; R = P*s;
a = b*M; R = P - Q; R = s*P;
a *= M; R = P + Q; R = P/s;
R *= Q; R = s*P;
R += Q; R *= s;
R -= Q; R /= s;
// 逐像素操作Vectorized operations on each element independently
// Eigen // Matlab //注释
R = P.cwiseProduct(Q); // R = P .* Q //逐元素乘法
R = P.array() * s.array(); // R = P .* s //逐元素乘法(s为标量)
R = P.cwiseQuotient(Q); // R = P ./ Q //逐元素除法
R = P.array() / Q.array(); // R = P ./ Q //逐元素除法
R = P.array() + s.array(); // R = P + s //逐元素加法(s为标量)
R = P.array() - s.array(); // R = P - s //逐元素减法(s为标量)
R.array() += s; // R = R + s //逐元素加法(s为标量)
R.array() -= s; // R = R - s //逐元素减法(s为标量)
R.array() < Q.array(); // R < Q //逐元素比较运算
R.array() <= Q.array(); // R <= Q //逐元素比较运算
R.cwiseInverse(); // 1 ./ P //逐元素取倒数
R.array().inverse(); // 1 ./ P //逐元素取倒数
R.array().sin() // sin(P) //逐元素计算正弦函数
R.array().cos() // cos(P) //逐元素计算余弦函数
R.array().pow(s) // P .^ s //逐元素计算幂函数
R.array().square() // P .^ 2 //逐元素计算平方
R.array().cube() // P .^ 3 //逐元素计算立方
R.cwiseSqrt() // sqrt(P) //逐元素计算平方根
R.array().sqrt() // sqrt(P) //逐元素计算平方根
R.array().exp() // exp(P) //逐元素计算指数函数
R.array().log() // log(P) //逐元素计算对数函数
R.cwiseMax(P) // max(R, P) //逐元素计算R和P的最大值
R.array().max(P.array()) // max(R, P) //逐元素计算R和P的最大值
R.cwiseMin(P) // min(R, P) //逐元素计算R和P的最小值
R.array().min(P.array()) // min(R, P) //逐元素计算R和P的最小值
R.cwiseAbs() // abs(P) //逐元素计算R和P的绝对值
R.array().abs() // abs(P) //逐元素计算绝对值
R.cwiseAbs2() // abs(P.^2) //逐元素计算平方
R.array().abs2() // abs(P.^2) //逐元素计算平方
(R.array() < s).select(P,Q ); // (R < s ? P : Q) //根据R的元素值是否小于s,选择P和Q的对应元素
R = (Q.array()==0).select(P,A) // R(Q==0) = P(Q==0) R(Q!=0) = P(Q!=0) //根据Q中元素等于零的位置选择P中元素
R = P.unaryExpr(ptr_fun(func)) // R = arrayfun(func, P) // 对P中的每个元素应用func函数
// Reductions.
int r, c;
// Eigen // Matlab //注释
R.minCoeff() // min(R(:)) //最小值
R.maxCoeff() // max(R(:)) //最大值
s = R.minCoeff(&r, &c) // [s, i] = min(R(:)); [r, c] = ind2sub(size(R), i); //计算最小值和它的位置
s = R.maxCoeff(&r, &c) // [s, i] = max(R(:)); [r, c] = ind2sub(size(R), i); //计算最大值和它的位置
R.sum() // sum(R(:)) //求和(所有元素)
R.colwise().sum() // sum(R) //按列求和
R.rowwise().sum() // sum(R, 2) or sum(R')' //按行求和
R.prod() // prod(R(:)) //累积
R.colwise().prod() // prod(R) //按列累积
R.rowwise().prod() // prod(R, 2) or prod(R')' //按行累积
R.trace() // trace(R) //迹
R.all() // all(R(:)) //是否所有元素都非零
R.colwise().all() // all(R) //按列判断,是否该列所有元素都非零
R.rowwise().all() // all(R, 2) //按行判断,是否该行所有元素都非零
R.any() // any(R(:)) //是否有元素非零
R.colwise().any() // any(R) //按列判断,是否该列有元素都非零
R.rowwise().any() // any(R, 2) //按行判断,是否该行有元素都非零
// 点积,范数等
// Eigen // Matlab // 注释
x.norm() // norm(x). //范数(注意:Eigen中没有norm(R))
x.squaredNorm() // dot(x, x) //平方和(注意:对于复数而言,不等价)
x.dot(y) // dot(x, y) //点积
x.cross(y) // cross(x, y) //交叉积,需要头文件 #include
类型转换
// Eigen // Matlab // 注释
A.cast(); // double(A) //变成双精度类型
A.cast(); // single(A) //变成单精度类型
A.cast(); // int32(A) //编程整型
A.real(); // real(A) //实部
A.imag(); // imag(A) //虚部
// 如果变换前后的类型相同,不做任何事情。
// 注意:Eigen中,绝大多数的涉及多个操作数的运算都要求操作数具有相同的类型
MatrixXf F = MatrixXf::Zero(3,3);
A += F; // 非法。Matlab中允许。(单精度+双精度)
A += F.cast(); // 将F转换成double,并累加。(一般都是在使用时临时转换)
// Eigen 可以将已存储数据的缓存 映射成 Eigen矩阵
float array[3];
Vector3f::Map(array).fill(10); // create a temporary Map over array and sets entries to 10
int data[4] = {1, 2, 3, 4};
Matrix2i mat2x2(data); // 将 data 复制到 mat2x2
Matrix2i::Map(data) = 2*mat2x2; // 使用 2*mat2x2 覆写data的元素
MatrixXi::Map(data, 2, 2) += mat2x2; // 将 mat2x2 加到 data的元素上 (当编译时不知道大小时,可选语法)