推导svm

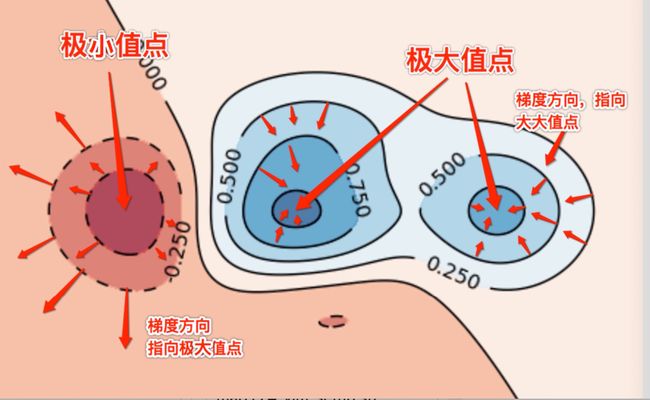
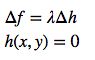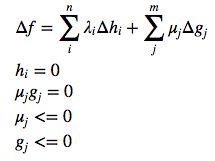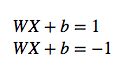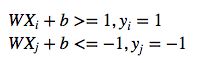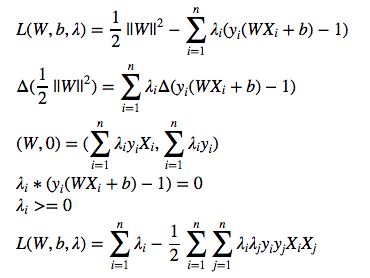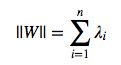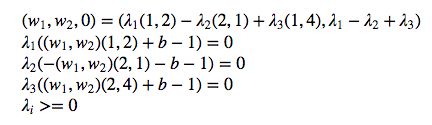梯度垂直于等高线，指向函数变化最快的方向，指向极大值点方向

约束条件为等式求极值

先来看个简单求极值例子

 h(x,y) = x+y-1=0,f(x,y) = (x-2)**2+(y-2)**2 

先看下图形z=f(x,y)等高线，以点(2,2)为圆形的同心圆

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D  


def f(X, Y):
    return (X-2)**2 + (Y-2)**2
x = np.arange(-5, 10, 0.1)
y = np.arange(-5, 10, 0.1)

# 可以使坐标轴等比例figsize=6,6
plt.figure(figsize=(6,6)) 
# 生成网格数据
X, Y = np.meshgrid(x, y)


# 填充等高线的颜色, 40是等高线分为几部分
plt.contourf(X, Y, f(X, Y), 40, alpha = 0.8, cmap = plt.cm.RdBu)
# 绘制等高线
#C = plt.contour(X, Y, f(X, Y),15, colors = 'black', linewidth = 0.5)
# 绘制等高线数据
plt.clabel(C, inline = True, fontsize = 10)
plt.plot(x, 1-x)
plt.ylim(-5,10)
plt.xlim(-5,10)
plt.show()

从图形的含义来说，f(x,y)表示的是点(2,2)点到可行域点{(x,y)|h(x,y)=0}的距离，可以看出最大值是无穷大，最小值就是点（2，2）到直线h(x,y)=0的垂直距离

从另一方面来说,极值点（x,y）,存在\lambda满足

可以从上式求的极小值点，可以通过判断二阶偏导数矩阵局部正定性，判断是极大值极小值。

对于多个约束条件，一般有拉格朗日定理

下面看看不等式约束，求极值，可行域变大了

• 1、边界上求的极值

• 2、可行域内部求的极值
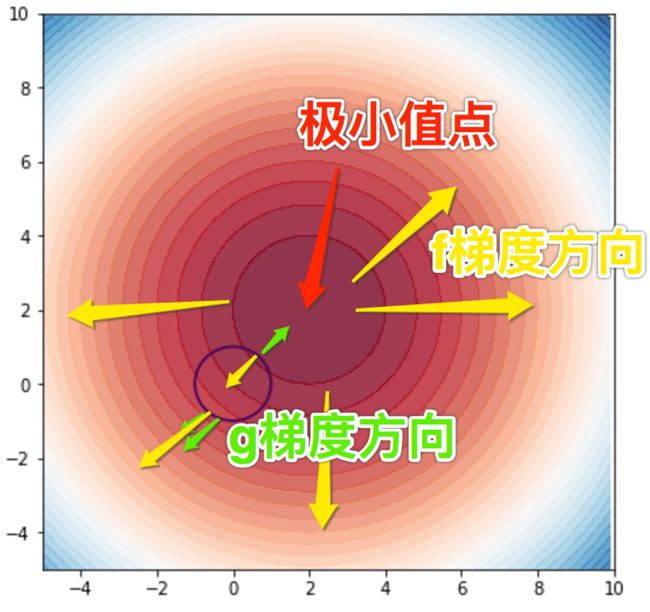
  看一个简单的例子

    f(x,y)=(x-2)**2+(y-2)**2,g(x,y)=x**2+y**2<=1
  

最小值点f的梯度等于0，从图中可以看出在可行域，梯度反向时取的最小值，梯度同向取的最大值，存在\lambda,使得

注意\lambda*g=0,还有个情况是f梯度等于0点在可行域范围内\lambda=0,\Delta(f)=0取得最小值，

更一般关系关系f,hi(x)=0,gj(x)<=0，就是一个线性组合

推导svm

SVM(Support Vector Machine)指的是支持向量机，是常见的一种判别方法。在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。

从图中可以看出满足分类要求分界线很多（高维数叫超平面），比如H1、H2，显然H1要比H2要好，H1最大化两个类别的距离，影响H1只是边界点，而之前线性分类器受整个数据影响.

假设H1是分界线，距离两个类别距离相同，边界上点满足

  实际来说边界上点不一定正好等与1或者-1，这里可以将等式右边化为1，例如边界点wx+b=c,
  两边同时除以c,w/cX+b/c=1，边界变为w/cX+b/c=0,这样处理会使我们方便很多        

两个边界线距离

要求距离最大值，转化为求||W||最小值，等价于求||W||最小值，看看有哪些约束条件

即

问题演变为

可以利用前面讨论不等式求极值

  （W,0）0是对b求偏导数，可以通过SMO算法求解,就出lambda大于0的，对应的X就是边界点，

利用上面等式就可求出

还有一个非常美的性质

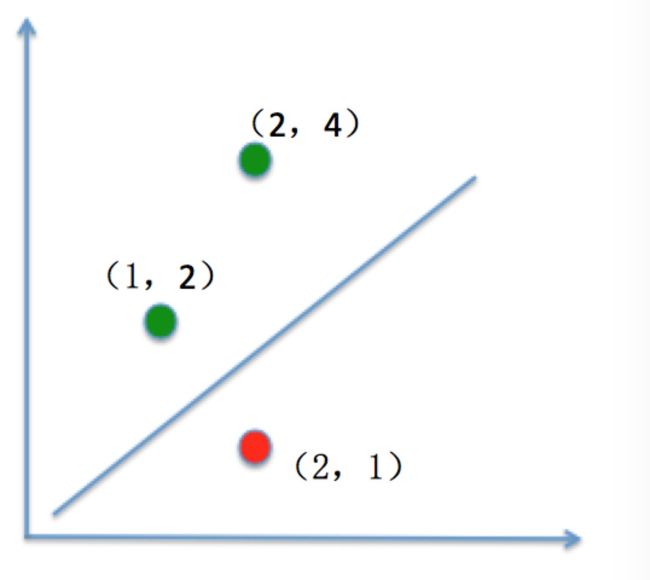
下面看一个简单的例子

适合红绿两个类分类直线很多，但是只有图中直线能都将两类之间距离达到最大,很明显直线方程为

                                   x-y=0

可以解出

SVM—线性不可分—核函数