机器学习调制解调器:ML将如何改变我们设计下一代通信系统的方式
所以,我听到你们都在问,我们都失业了吗?通信工程师是机器崛起的又一个受害者吗?幸运的是,本文中的答案是否定的。但是Nathan, Ben和Tim指出了一种新的方式来指定和设计通信系统,这可能会永远改变我们标准化、设计和优化产品的方式。是时候学习你去年一直在推迟的“ML基础”在线课程了。
Adapting the Wireless Physical Layer from End-to-End using Channel Autoencoders and Deep Learning
通信系统中自由度的增长
通信系统在过去的40年里发展迅速,不断推进调制技术、纠错技术和其他物理层技术来提高系统性能。随着算法复杂度、设备数量、天线数量、频带数量、资源分配调度、集成无线电芯片复杂度、系统参数总数不断增加,在所有这些自由度上进行全局优化的任务越来越艰巨。
无线电算法设计是一个高度复杂的、划分的过程,在设计过程中,错误校正码、大规模MIMO算法、同步和估计等技术常常被逐一分析,然后串联起来形成完整的调制解调器系统。使用严格的分析概率方法来优化完整的调制解调器系统也是非常困难的,特别是在考虑复杂的通道模型和其他因素的影响时,例如硬件非线性、结构干扰和其他传统的噪声或衰落模型难以建模的影响时。更严格的模型如指定测试ITU / 3 gpp系统仍然大大简化衰落的影响且不准确地捕捉许多现代部署[7]的影响,但是当试图考虑它们对信号处理函数级联的联合影响, 和寻求共同调整和优化每一个子系统也是非常复杂和繁琐的。
一般来说,这些趋势导致了当今通信系统的高度复杂性,在简单信道的假设下,我们非常接近单用户的香农容量,但在考虑所有可用自由度时,我们还没有完全获得剩余的性能收益。存在改进潜力的几个关键领域包括: 通过合并和逼近现有的函数来降低计算复杂度 ,利用通过物理层的错误反馈来提高性能 ,更好地补偿来自结构化失真和干扰源的干扰 ,改进最大化多用户和多天线容量的算法 ,以及改进共享系统中有限资源的调度和分配 。
如何应对复杂度:一种用于物理层设计的学习方法
联合优化传输比特与接收比特之间物理层的信号处理算法 (端到端优化) ,在现实的无线电影响、失真、干扰和其他障碍下从来都不实用。 如使用迭代方法[10]对接收机功能的进行联合优化(如同步、均衡、符号估计和解码) 来提高性能,但这样做通常需要较高的计算成本和相对简化的影响模型。
相比之下,近年来,尤其在计算机视觉领域, 基于数据的图像处理算法的高度复杂级联的端到端优化趋势和全局损失函数的使用通过机器学习(ML)技术的集合已经变得易于处理且处于最先进的水平。关于像素级视觉任务、目标检测和标记以及车道跟踪等任务的回归等所有决策流形的联合估计都已被证明是可行的,并且在自动驾驶汽车等应用中处于最先进的水平。
使用数据、模拟和经验来指导高度复杂的软件和算法任务的端到端综合已越来越多地在一些关键的信息处理领域被采用, 最近在特斯拉人工智能主管安德烈•卡帕西(Andrej Karpathy)撰写的一篇雄文([11])中被称为“软件2.0” 。
两年前在[2]中,我们将同样的思想应用于物理层通信系统的合成问题,将“通信基础问题”[13]作为端到端优化的机器学习任务 ,我们为了一个简单的目标而试图优化一个具有多个自由度的大型非线性神经网络,重建一个随机输入信号,通过一个通道传输和接收,以及在接收方输出。在神经网络中输入重构的任务,就是所谓的自动编码器(AE) 。
自动编码器和现代非线性神经网络结构
最近在深度学习领域,autoencoders已经被用来完成图像的相似检测,对包含编码器和解码器网络的一系列非线性神经元层进行优化,将每组输入数据转换为学习到的隐藏特征(降维),然后把它重构成原始输入数据。当隐藏层特征形式为一组分布而不是值时,这被称为变分自编码器(VAE)。这些方法可以有很多很好的特性,例如去除输入数据的非结构成分的去噪效果,并且可以产生非常有用的信号的非线性稀疏特征,用于压缩和学习能够表示输入数据复杂高维特性的潜在特征。 在编码器和解码器网络中使用的神经网络结构有很大的不同,但在最简单的形式下, 它们包括一系列使用随机值(w)和偏置值(b)的连续乘积和累加操作, 在经过非线性激活函数,如经过修正的线性单元(RELU)(由f(x) = max(0,x)给出)。 下面是一个简单的网络,几个全连接层使用一组网络参数(θ)将值从输入“前向传播”到输出,这种情况下组成的w和b在训练期间进行迭代更新。

网络参数的训练过程涉及损失函数(L)的计算, 在这种情况下,计算输入值和输出值之差, 然后最小化网络中所有参数的损失函数。 这可以通过使用随机梯度下降(SGD)来实现, 或者是其中的一种变体(比如Adam[13]),对于大型网络来说,这种变体的收敛速度更快。衡量输入输出之差常常考虑平均平方误差(mean-squared error, MSE), 但是对于分类问题,比如传输码字的选择或者其他离散类, 当与适当的输出激活函数(如SoftMax)结合时,交叉熵是一种有效的选择。 在一系列迭代或epoch中迭代更新网络参数的过程中, 不断地计算每个元素的梯度dL / dθ, 并使用一些学习速率(η) 更新值,当参数在第i个epoch时为θi =θi-1 -η* dL / dθ。 计算这个梯度可以使用通过网络向后的链式法则,通常被称为“反向传播”。 这些基本原理在神经网络中多年来一直是相同的,但最近在计算能力、SGD效能、正则化和非线性选择方面的进展使这一训练过程在更大的网络中得以实现。 在更大的网络上一起使用所有这些技术,现在通常被称为深度学习。
信道自动编码器
我们通过插入一个信道模型构造一个信道自动编码器,表示通信系统中进入传统自编码器或变分自编码器的隐层的损耗 ,通过选择一组比特或码字(s),这些码字包含我们想要发送和重构的信息,作为我们的输入和输出。 通过这种方式构造一个自动编码器,训练使网络在某种基础函数(I/Q样本、OFDM载波等)上学习一个信号传输表示(x),它可以从它的接收形式(y)中解码来估计s的值。与典型的自动编码器用法相比,我们可能不关心把s压缩成x,而是寻找一种适合于射频传输和对相关通道的影响有弹性的表示 (例如噪音、衰落、偏移)。这样,我们就可以以端到端的方式联合优化完整的编码或调制过程以及解码或解调过程,从而尽可能简单地重构s,从而最小化系统的比特或符号错误率。

该通道自动编码器的一般形式如上图所示,在[2]中有更深入的描述。 在其最简单形式中,信道可能只包括加性高斯白噪声, 然而,高度非线性或随机函数或如放大器近似模型或干扰源的影响可以用专业的无线传播领域的知识来建模以及如何使用数字信号处理对它们进行建模 (使专业的无线和DSP领域知识仍然是使这些系统一起工作的核心技能,即使当大量使用机器学习(学习)来优化它们)。 但是,需要注意的是,对于这种网络的反向传播和联合端到端SGD优化,信道影响的表达式必须是可微的,以便在优化过程中可以方便地计算正向和反向传播。
下面我们展示了一个这样的解决方案,使用信道自动编码器,为一个5bit的信息s在带有高斯噪声和AM/AM和AM/PM失真以及相位噪声的微非线性信道上传输找到一个隐藏的特征或者说调制/编码。
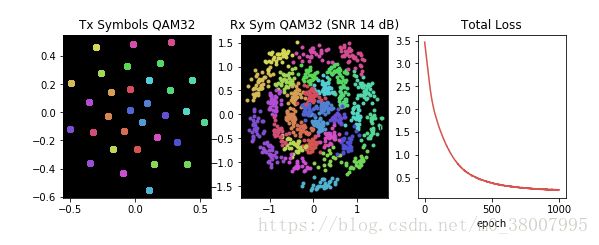
这个解决方案是优雅的,对于一组复杂的信道影响模型,它使用一个相对简单的基于SGD的方法很快地收敛到了一个非常有效的解,因为采用一套更传统的精确分析优化方法来得到精确的最优解将会非常繁琐和耗时。 同样需要注意的是在一个真正的无线信道上,这实际上仍然是一个非常简单的通道模型,它只关注单符号优化(而不是符号块或更大的码字), 单个发射和接收天线,不存在任何干扰或其他影响。
然而,这种方法引发了一系列新的问题,比如,我如何选择我的网络架构和超参数设置,我怎样才能用SGD 训练这个网络,我应该在哪个信噪比和随机损耗模型的状态下进行训练, 等等,所有这些都是很大程度上仍未解决的问题,短期内不太可能有确切的解决方案 (许多问题也可以通过近似的迭代解决,而不是实际的)。 这些问题中的许多都是在整个机器学习领域共同存在的, 并且有可以遵循的最优方法和严格的统计分析来解决它们在许多应用领域的应用, 但其中一些是通信专有的,并在我们的领域内提出了极好的开放研究的问题。
不过,这个解决方案也有一些非常好的新特性。首先,网络的计算复杂度是由网络的大小来定义的,因此通过选择架构,可以很容易地对准确性和计算性能进行交换。 这种计算复杂度通常也较低,因为它近似于一个端到端流形或映射问题的解 ,而不是将其划分为级联函数之间的严格的可解释接口(例如明显的以awgn为中心的星座映射和预失真应用) 。最后,它学到的解决方案本来就是前向反馈和并行的, 这意味着网络值可以通过数据并行性来计算, 这种迭代或循环是不需要的,帮助快速映射到高效的低时钟率、高效的并发架构,同时确保低固定延迟算法的出现。
复杂度的拓展和剩余问题的解决
有趣的是,在过去的一年里,对这种物理层设计方法最近开始得到研究人员更广泛的兴趣和应用。在[1-5,8-9,14-15]的工作和其他一些人进一步拓展了这个基本方法 如考虑到多天线系统的复杂性增加,学习基于信道状态信息的预编码能力, 在高度非线性或非传统信道介质下的性能, 以及如何在实际传输部署设备中实现、审查和优化这种基本系统方法。 以上的每一个都考虑了一组新的信道影响和系统约束,它们在特定的通信系统中是有意义的, 需要重要的领域知识和模型来构建, 但是大量利用这种基本方法以端到端方式进行优化,能够不用考虑模型中引入的所有复杂度找到一个全局优化和定制的编码解决方案,来最大限度地提高系统性能。
在这一相对较新和广泛开放的研究领域,仍然存在许多挑战和机会。 尽管我们已经提出了几个解决方案,但在实际信道中和黑盒信道函数上的调参系统对于没有封闭形式解析解(或相应梯度)的系统仍然是一个挑战。 在分布式和部署系统中的错误反馈和训练的编排仍然是在线适应此类系统的一个挑战。 可伸缩性学习的码字大小可以达到非常大的块,架构选择、训练过程和许多其他领域的最优方法对于这类系统的成熟、最终部署和完全实现仍然很重要。
然而,这种方法对相当复杂的损伤效应组合产生近似解的能力,对于许多可能的通信系统应用来说已经是相对有效的。
然而,这种方法对于相当复杂的各种信道影响的组合得到近似解的能力,对于许多可能的通信系统应用来说,已经具有相对的影响力。机器学习不会很快取代传统的通信和数字信号处理, 如果真的替代的话,专业知识,理解和信道影响因素的建模对于它的有效使用是绝对关键的。 然而,对于任何试图优化复杂的现实世界系统的通信工程师来说,ML正迅速成为一种强制性的、核心的技能,就像它对地球上几乎所有其他领域一样。 虽然对简化模型的精确求解一直是通信中许多问题的规范和普遍做法, 很重要的一点是当我们用模型的复杂性换取解决方案的准确性并继续构建越来越好的近似系统时, 会受到乔治·鲍克斯永恒的咒语, “all models are wrong, but some are useful。” 即使通信问题的精确解决方案一直都是错误的,但随着我们能够近距离捕捉、建模和优化更多的真实自然效果,最终的系统解决方案将会变得越来越有用。
转载于:
https://www.comsoc.org/ctn/machine-learning-modems-how-ml-will-change-how-we-specify-and-design-next-generation
References
- T. O’Shea, and T. Roy, and N. West, and B. Hilburn, “Physical Layer Communications System Design Over-the-Air Using Adversarial Networks,” under submission.
- O’Shea, Timothy, and Jakob Hoydis. “An introduction to deep learning for the physical layer.” IEEE Transactions on Cognitive Communications and Networking 3.4 (2017): 563-575.
- H. Ye, G. Y. Li, and B.-H. Juang, “Power of deep learning for channel estimation and signal detection in OFDM systems,” IEEE Wireless Communications Letters, vol. 7, no. 1, pp. 114 -117, February 2018.
- A. Felix, and S. Cammerer, and S. Dorner, and J. Hoydis, and Stephan ten Brink, “OFDM-Autoencoder for End-to-End Learning of Communications Systems,” submitted to SPAWC 2018.
- S. Dorner, and S. Cammerer, and J. Hoydis, and Stephan ten Brink, “Deep Learning Based Communication Over the Air,” IEEE Journal of Selected Topics in Signal Processing, vol 12, no. 1, pp. 132-143, February 2018.
- E. Björnson, “A View of the Way Forward in 5G From Academia,” ComSoc Technology News https://www.comsoc.org/ctn/view-way-forward-5g-academia
- H. Asplund, K. Larsson and P. Okvist, “How Typical is the “Typical Urban” channel model?,” VTC Spring 2008 - IEEE Vehicular Technology Conference, Singapore, 2008, pp. 340-343. https://www.ericsson.com/assets/local/publications/conference-papers/typical_urban_channel_model.pdf
- Lee, Hoon, Inkyu Lee, and Sang Hyun Lee. “Deep learning based transceiver design for multi-colored VLC systems.” Optics express 26.5 (2018): 6222-6238
- Huang, Sihao, and Haowen Lin. “Fully Optical Spacecraft Communications: Implementing an Omnidirectional PV-Cell Receiver and 8Mb/s LED Visible Light Downlink with Deep Learning Error Correction.” arXiv preprint arXiv:1709.03222 (2017).
- Wymeersch, Henk. Iterative receiver design. Vol. 234. Cambridge: Cambridge University Press, 2007.
- Karpathy, Andrej, “Software 2.0”, https://medium.com/@karpathy/software-2-0-a64152b37c35
- Shannon, Claude Elwood. “A mathematical theory of communication.” Bell system technical journal 27.3 (1948): 379-423.
- Kingma, Diederik P., and Jimmy Ba. “Adam: A method for stochastic optimization.” arXiv preprint arXiv:1412.6980 (2014).
- O’Shea, Timothy J., Tugba Erpek, and T. Charles Clancy. “Deep learning based MIMO communications.” arXiv preprint arXiv:1707.07980 (2017).
- Farsad, Nariman, and Andrea Goldsmith. “Detection algorithms for communication systems using deep learning.” arXiv preprint arXiv:1705.08044 (2017).