Minimum Snap轨迹规划详解（1）轨迹规划入门

1. 轨迹规划是什么？

在机器人导航过程中，如何控制机器人从A点移动到B点，通常称之为运动规划。运动规划一般又分为两步：

1. 路径规划：在地图（栅格地图、四\八叉树、RRT地图等）中搜索一条从A点到B点的路径，由一系列离散的空间点（waypoint）组成。
2. 轨迹规划：由于路径点可能比较稀疏、而且不平滑，为了能更好的控制机器人运动，需要将稀疏的路径点变成平滑的曲线或稠密的轨迹点，也就是轨迹。

2. 轨迹是什么？

轨迹一般用n阶多项式(polynomial)来表示，即

p(t)=p0+p1t+p2t2...+pntn=∑i=0npiti

其中 p0,p1,...,pn 为轨迹参数（n+1个），设参数向量 p=[p0,p1,...,pn]T ，则轨迹可以写成向量形式，

p(t)=[1,t,t2,...,tn]⋅p

对于任意时刻 t ，可以根据参数计算出轨迹的位置P(osition)，速度V(elocity)，加速度A(cceleration)，jerk，snap等。

v(t)=p′(t)=[0,1,2t,3t2,4t3,...,ntn−1]⋅pa(t)=p′′(t)=[0,0,2,6t,12t2,...,n(n−1)tn−2]⋅pjerk(t)=p(3)(t)=[0,0,0,6,24t,...,n!(n−3!)tn−3]⋅psnap(t)=p(4)(t)=[0,0,0,0,24,...,n!(n−4!)tn−4]⋅p

一个多项式曲线过于简单，一段复杂的轨迹很难用一个多项式表示，所以将轨迹按时间分成多段，每段各用一条多项式曲线表示，形如：

p(t)=⎧⎩⎨⎪⎪⎪⎪⎪⎪[1,t,t2,...,tn]⋅p1   t0≤t<t1[1,t,t2,...,tn]⋅p2   t1≤t<t2...[1,t,t2,...,tn]⋅pk   tk−1≤t<tk

k 为轨迹的段数， pi=[pi0,pi1,...,pin]T 为第i段轨迹的参数向量。

此外，实际问题中的轨迹往往是二维、三维甚至更高维，通常每个维度单独求解轨迹。

3. Minimum Snap轨迹规划

轨迹规划的目的：求轨迹的多项式参数 p1,...,pk 。
我们可能希望轨迹满足一系列的约束条件，比如：希望设定起点和终点的位置、速度或加速度，希望相邻轨迹连接处平滑（位置连续、速度连续等），希望轨迹经过某些路径点，设定最大速度、最大加速度等，甚至是希望轨迹在规定空间内（corridor）等等。
通常满足约束条件的轨迹有无数条，而实际问题中，往往需要一条特定的轨迹，所以又需要构建一个最优的函数，在可行的轨迹中找出“最优”的那条特定的轨迹。
所以，我们将问题建模（fomulate）成一个约束优化问题，形如：

minf(p)s.t.  Aeqp=beq,        Aieqp≤bieq

这样，就可以通过最优化的方法求解出目标轨迹参数 p 。 注意：这里的轨迹参数 p 是多端polynomial组成的大参数向量 p=[pT1,pT2,...,pTk]T 。
我们要做的就是： 将优化问题中的 f(p) 函数和 Aeq,beq,Aieq,bieq 参数给列出来，然后丢到优化器中求解轨迹参数p。
Minimum Snap顾名思义，Minimum Snap中的最小化目标函数是Snap（加加加速度），当然你也可以最小化Acceleration（加速度）或者Jerk（加加速度），至于它们之间有什么区别，quora上有讨论。一般不会最小化速度。

minimum snap: minf(p)=min(p(4)(t))2minimum jerk: minf(p)=min(p(3)(t))2minimum acce: minf(p)=min(p(2)(t))2

4. 一个简单的例子

给定包含起点终点在内的k+1个二维路径点 pt0,pt1,...,ptk，pti=(xi,yi) ，给定起始速度和加速度为 v0,a0 ，末端加速度为 ve,ae ，给定时间T，规划出经过所有路径点的平滑轨迹。

a. 初始轨迹分段与时间分配

根据路径点，将轨迹分为k段，计算每段的距离，按距离平分时间T(匀速时间分配)，得到时间序列 t0,t1,...,tk 。对x,y维度单独规划轨迹。后面只讨论一个维度。
时间分配的方法：匀速分配或梯形分配，假设每段polynomial内速度满足匀速或梯形速度变化，根据每段的距离将总时间T分配到每段。
这里的轨迹分段和时间分配都是初始分配，在迭代算法中，如果corridor check和feasibility check不满足条件，会插点或增大某一段的时间，这个后续细说。

b. 构建优化函数

Minimum Snap的优化函数为：

min∫T0(p(4)(t))2dt=min∑i=1k∫titi−1(p(4)(t))2dt=min∑i=1k∫titi−1([0,0,0,0,24,...,n!(n−4!)tn−4]⋅p)T[0,0,0,0,24,...,n!(n−4!)tn−4]⋅p dt=min∑i=1kpT∫titi−1[0,0,0,0,24,...,n!(n−4!)tn−4]T[0,0,0,0,24,...,n!(n−4!)tn−4] dt p=min∑i=1kpTQip

其中，

Qi=∫titi−1[0,0,0,0,24,...,n!(n−4!)tn−4]T[0,0,0,0,24,...,n!(n−4!)tn−4] dt=⎡⎣⎢04×40(n−3)×404×(n−3)r!(r−4)!c!(c−4)!1(r−4)+(c−4)+1(t(r+c−7)i−t(r+c−7)i−1)⎤⎦⎥

注意：r,c为矩阵的行索引和列索引， 索引从0开始，即第一行r=0。

Q=⎡⎣⎢⎢⎢⎢⎢Q1Q2⋱Qk⎤⎦⎥⎥⎥⎥⎥minpTQp

可以看到，问题建模成了一个数学上的二次规划（Quadratic Programming，QP）问题。

c. 构建等式约束方程

1. 设定某一个点的位置、速度、加速度或者更高为一个特定的值，可以构成一个等式约束。例如：
   
   位置约束：[1,t0,t20,...,tn0,0...0(k−1)(n+1)]p=p0速度约束：[0,1,2t0,...,ntn−10,0...0(k−1)(n+1)]p=v0加速度约束：[0,0,2,...,n(n−1)tn−20,0...0(k−1)(n+1)]p=a0
   
   由于要过中间点，对中间点的位置也构建等式约束，方法同上。
2. 相邻段之间的位置、速度、加速度连续可以构成一个等式约束，例如第i、i+1段的位置连续构成的等式约束为
   
   [0...0(i−1)(n+1),1,ti,t2i,...,tni,−1,−ti,−t2i,...,−tni,0...0(k−i−1)(n+1)]p=0
   
   速度、加速度连续类似，不再罗列。

合并所有等式约束，得到

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢1,t0,t20,...,tn0,0...0(k−1)(n+1)0,1,2t0,...,ntn−10,0...0(k−1)(n+1)0,0,2,...,n(n−1)tn−20,0...0(k−1)(n+1)⋮0...0(i−1)(n+1),1,ti,t2i,...,tni,0...0(k−i)(n+1)⋮0...0(k−1)(n+1),1,tk,t2k,...,tnk0...0(k−1)(n+1),0,1,2tk,...,ntn−1k0...0(k−1)(n+1),0,0,2,...,n(n−1)tn−2k0...0(i−1)(n+1),1,ti,t2i,...,tni,−1,−ti,−t2i,...,−tni,0...0(k−i−1)(n+1)0...0(i−1)(n+1),0,1,2ti,...,ntn−1i,−0,−1,−2ti,...,−ntn−1i,0...0(k−i−1)(n+1)0...0(i−1)(n+1),0,0,2,...,n!(n−2)!tn−2i,−0,−0,−2,...,−n!(n−2)!tn−2i,0...0(k−i−1)(n+1)⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥(4k+2)×(n+1)kp=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢p0v0a0⋮pi⋮pkvkak0⋮0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

等式约束个数=3（起始PVA）+k-1（中间点的p）+3（终点pva）+3(k-1)（中间点PVA连续）=4k+2

d. 构建不等式约束

不等式约束与等式约束类似，也是设置某个点的P、V、A小于某一特定值，从而构建 Aieqp=bieq ，不等式约束一般是在corridor中用的比较多，这里暂时先不使用不等式约束。

e. 求解

利用QP求解器进行求解，在MATLAB中可以使用quadprog() 函数，C++的QP求解器如OOQP，也可以自己去网上找。

实验结果

MATLAB代码在这里。
优化列表：

 min：snap
 等式约束：起点pva，终点pva，中间点的p，中间点pva连续
 不等式约束：无

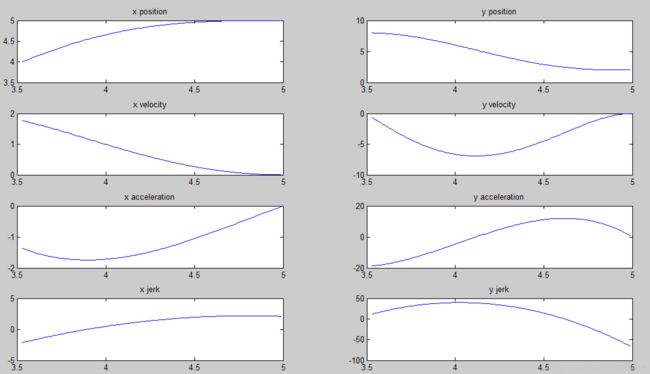
生成x、y两个维度的轨迹，合并后如下图所示。包含起始终止共5个点，用四段poly来描述，中间点也就是poly之间的交界点。

5. 轨迹怎么用？（轨迹跟踪）

至此，我们已经求得了轨迹（很多段高阶多项式的参数），但怎么用来控制机器人运动呢？轨迹跟踪是：根据轨迹和机器人当前状态（当前位置、速度、加速度），输出机器人控制指令（速度、加速度、角速度等），控制机器人沿着轨迹运动。有很多种跟踪方法

• 最简单的跟踪方法是位置控制：计算轨迹上离当前位置最近的点，以最近点为期望位置做位置控制，即 v=kp(pnearest−pcur)
• Minimum Snap中的前馈控制：计算轨迹上离最近点的（位置 pe 、速度 ve 、加速度 ae ），
  
  速度指令：v加速度前馈：a=ve=ae+kp(pe−pcur)+kd(ve−vcur)

6. 小结

1. 轨迹规划问题通常建模成一个带约束的二次规划（QP）问题来求解，优化函数可以是snap、jerk、acceleration及它们的组合或其他任何能够formulate成 pTQp 形式的函数，约束包括等式约束和不等式约束。
2. 轨迹规划中默认时间t已知，通常根据期望速度和总路程计算一个总时间T，再按照匀速运动和梯形速度曲线分配到每段polynomial上。
3. 上面例子中规划出的轨迹并不是很好，有以下问题：
   a) 轨迹与路径相差有点大，而且在第三个waypoint处会有打结的现象；
   b) y轴的加速度非常大（接近 20m/s2 ），超过了机器人的最大加速度。实际轨迹需要进行feasibility check（可行性检测），确保满足工程可行性，比如最大速度、最大角速度限制等。
4. 这两个问题的根本原因在于时间给的不合理，时间分配是轨迹规划中比较蛋疼的问题，给的时间太小，速度、加速度自然就很大，两段时间分配不当就会生成打结的轨迹。下一节，专门讨论时间分配问题。

参考文献

1. Richter C, Bry A, Roy N. Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments[M]//Robotics Research. Springer International Publishing, 2016: 649-666.
2. Vijay Kumar的一系列论文：Mellinger D, Kumar V. Minimum snap trajectory generation and control for quadrotors[C]//Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011: 2520-2525.