模拟退火算法解决TSP问题

旅行商问题的几种求解：https://wenku.baidu.com/view/0579c5206294dd88d1d26b70.html
模拟退火法解决TSP及Matlab实现：https://www.cnblogs.com/youngsea/p/7461977.html
模拟退火法TSP问题的Python实现：https://blog.csdn.net/qq_34798326/article/details/79013338

一、旅行商问题

1. 问题描述：一名商人要到若干城市去推销商品，已知城市个数和各城市间的路程（或旅费），要求找到一条从城市1出发，经过所有城市且每个城市只能访问一次，最后回到城市1的路线，使总的路程（或旅费）最小。
2. 问题分析：该问题是组合优化问题，属于NP难题，是诸多领域内出现的多种复杂问题的集中概括和简化形式，并且已成为各种启发式的搜索、优化算法的间接比较标准。

（图片来源https://www.cnblogs.com/youngsea/p/7461977.html）

二、 模拟退火算法

1. 算法
模拟退火算法可分为解空间、目标函数和初始解三部分，其基本思想是：
（1）初始化：初始温度T(充分大)，初始解状态s(是算法迭代的起点)，每个T值的迭代次数L；
（2）对k=1，……，L做第(3)至第6步；
（3）产生新解s′；
（4）计算增量cost=cost(s′)-cost(s)，其中cost(s)为评价函数；
（5）若t<0则接受s′作为新的当前解，否则以概率exp(-t′/T)接受s′作为新的当前解；
（6）如果满足终止条件则输出当前解作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法；
（7）T逐渐减少，且T趋于0，然后转第2步运算。

2. 参数选择
（1）温度T的初始值设置。
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一。初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。
（2）温度衰减函数的选取。
衰减函数用于控制温度的退火速度，一个常用的函数为：
T(t+1)=aT(t)
式中a是一个非常接近于1的常数，t为降温的次数。
（3）马尔可夫链长度L的选取。
通常的原则是：在衰减参数T的衰减函数已选定的前提下，L的选取应遵循在控制参数的每一取值上都能恢复准平衡的原则。

三、TSP算法实现

1. TSP算法描述
（1）TSP问题的解空间和初始解
TSP的解空间S是遍访每个城市恰好一次的所有回路，是所有城市排列的集合。TSP问题的解空间S可表示为{1,2,…,n}的所有排列的集合，即S = {(c1,c2,…,cn) | ((c1,c2,…,cn)为{1,2,…,n}的排列）}，其中每一个排列Si表示遍访n个城市的一个路径，ci= j表示在第i次访问城市j。模拟退火算法的最优解与初始状态无关，故初始解为随机函数生成一个{1,2,…,n}的随机排列作为S0。
（2）目标函数
TSP问题的目标函数即为访问所有城市的路径总长度，也可称为代价函数：

现在TSP问题的求解就是通过模拟退火算法求出目标函数C(c1,c2,…,cn)的最小值，相应地，s*= (c*1,c*2,…,c*n)即为TSP问题的最优解。
（3）新解产生
新解的产生对问题的求解非常重要。新解可通过分别或者交替用以下2种方法产生：
①二变换法：任选序号u,v(设uvn)，交换u和v之间的访问顺序，若交换前的解为si= (c1,c2,…,cu,…,cv,…,cn),交换后的路径为新路径，即：

②三变换法：任选序号u,v和ω(u≤vω)，将u和v之间的路径插到ω之后访问，若交换前的解为si= (c1,c2,…,cu,…,cv,…,cω,…,cn)，交换后的路径为的新路径为：

（4）目标函数差
计算变换前的解和变换后目标函数的差值：

（5）Metropolis接受准则
根据目标函数的差值和概率exp(-ΔC′/T)接受si′作为新的当前解si，接受准则：

2 TSP算法流程
根据以上对TSP的算法描述，可以写出用模拟退火算法解TSP问题的流程图2 所示：

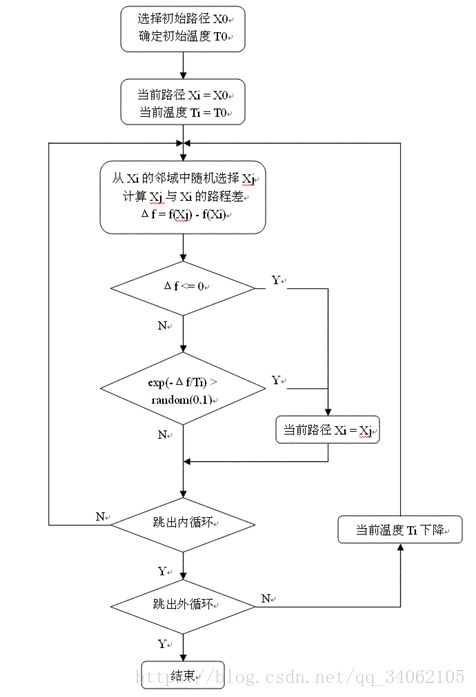
3. Python实现

import numpy as np
import matplotlib.pyplot as plt 
import pdb

"旅行商问题 ( TSP , Traveling Salesman Problem )"
coordinates = np.array([[565.0,575.0],[25.0,185.0],[345.0,750.0],[945.0,685.0],[845.0,655.0],
                        [880.0,660.0],[25.0,230.0],[525.0,1000.0],[580.0,1175.0],[650.0,1130.0],
                        [1605.0,620.0],[1220.0,580.0],[1465.0,200.0],[1530.0,  5.0],[845.0,680.0],
                        [725.0,370.0],[145.0,665.0],[415.0,635.0],[510.0,875.0],[560.0,365.0],
                        [300.0,465.0],[520.0,585.0],[480.0,415.0],[835.0,625.0],[975.0,580.0],
                        [1215.0,245.0],[1320.0,315.0],[1250.0,400.0],[660.0,180.0],[410.0,250.0],
                        [420.0,555.0],[575.0,665.0],[1150.0,1160.0],[700.0,580.0],[685.0,595.0],
                        [685.0,610.0],[770.0,610.0],[795.0,645.0],[720.0,635.0],[760.0,650.0],
                        [475.0,960.0],[95.0,260.0],[875.0,920.0],[700.0,500.0],[555.0,815.0],
                        [830.0,485.0],[1170.0, 65.0],[830.0,610.0],[605.0,625.0],[595.0,360.0],
                        [1340.0,725.0],[1740.0,245.0]])

#得到距离矩阵的函数
def getdistmat(coordinates):
    num = coordinates.shape[0] #52个坐标点
    distmat = np.zeros((52,52)) #52X52距离矩阵
    for i in range(num):
        for j in range(i,num):
            distmat[i][j] = distmat[j][i]=np.linalg.norm(coordinates[i]-coordinates[j])
    return distmat

def initpara():
    alpha = 0.99
    t = (1,100)
    markovlen = 1000

    return alpha,t,markovlen
num = coordinates.shape[0]
distmat = getdistmat(coordinates) #得到距离矩阵


solutionnew = np.arange(num)
#valuenew = np.max(num)

solutioncurrent = solutionnew.copy()
valuecurrent =99000  #np.max这样的源代码可能同样是因为版本问题被当做函数不能正确使用，应取一个较大值作为初始值
#print(valuecurrent)

solutionbest = solutionnew.copy()
valuebest = 99000 #np.max

alpha,t2,markovlen = initpara()
t = t2[1]

result = [] #记录迭代过程中的最优解
while t > t2[0]:
    for i in np.arange(markovlen):

        #下面的两交换和三角换是两种扰动方式，用于产生新解
        if np.random.rand() > 0.5:# 交换路径中的这2个节点的顺序
            # np.random.rand()产生[0, 1)区间的均匀随机数
            while True:#产生两个不同的随机数
                loc1 = np.int(np.ceil(np.random.rand()*(num-1)))
                loc2 = np.int(np.ceil(np.random.rand()*(num-1)))
                ## print(loc1,loc2)
                if loc1 != loc2:
                    break
            solutionnew[loc1],solutionnew[loc2] = solutionnew[loc2],solutionnew[loc1]
        else: #三交换
            while True:
                loc1 = np.int(np.ceil(np.random.rand()*(num-1)))
                loc2 = np.int(np.ceil(np.random.rand()*(num-1))) 
                loc3 = np.int(np.ceil(np.random.rand()*(num-1)))

                if((loc1 != loc2)&(loc2 != loc3)&(loc1 != loc3)):
                    break

            # 下面的三个判断语句使得loc1
            if loc1 > loc2:
                loc1,loc2 = loc2,loc1
            if loc2 > loc3:
                loc2,loc3 = loc3,loc2
            if loc1 > loc2:
                loc1,loc2 = loc2,loc1

            #下面的三行代码将[loc1,loc2)区间的数据插入到loc3之后
            tmplist = solutionnew[loc1:loc2].copy()
            solutionnew[loc1:loc3-loc2+1+loc1] = solutionnew[loc2:loc3+1].copy()
            solutionnew[loc3-loc2+1+loc1:loc3+1] = tmplist.copy()  

        valuenew = 0
        for i in range(num-1):
            valuenew += distmat[solutionnew[i]][solutionnew[i+1]]
        valuenew += distmat[solutionnew[0]][solutionnew[51]]
       # print (valuenew)
        if valuenew#接受该解

            #更新solutioncurrent 和solutionbest
            valuecurrent = valuenew
            solutioncurrent = solutionnew.copy()

            if valuenew < valuebest:
                valuebest = valuenew
                solutionbest = solutionnew.copy()
        else:#按一定的概率接受该解
            if np.random.rand() < np.exp(-(valuenew-valuecurrent)/t):
                valuecurrent = valuenew
                solutioncurrent = solutionnew.copy()
            else:
                solutionnew = solutioncurrent.copy()
    t = alpha*t
    result.append(valuebest)
    print (t) #程序运行时间较长，打印t来监视程序进展速度
#用来显示结果
plt.plot(np.array(result))
plt.ylabel("bestvalue")
plt.xlabel("t")
plt.show()