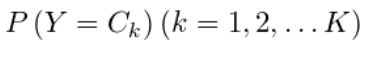传统机器学习

朴素贝叶斯原理：

 

朴素贝叶斯是基于贝叶斯定理和特征条件独立假设分类方法。对于给定训练集，首先基于特征条件独立性的假设，学习输入/输出联合概率（计算出先验概率和条件概率，然后求出联合概率）。然后基于此模型，给定输入x，利用贝叶斯概率定理求出最大的后验概率作为输出y。

假设我们有训练数据集如下：

即有m个样本，每个样本有n个特征，特征输出有K个类型，定义为C1、C2、... CK。

于是，从样本中可以得出朴素贝叶斯的先验分布：

接着学习到条件概率分布：

然后根据贝叶斯公式就可以得到XY的联合分布：

 

 

朴素贝叶斯模型假设X的n个维度之间相互独立，则有：

朴素贝叶斯文本分类代码：

import mathfrom collections

import defaultdict  

class NBayes(object):    

def __init__(self, trainSet):      

 self.data = trainSet      

 self.tags = defaultdict(int)        

self.tagwords = defaultdict(int)        

self.total = 0    

def _tokenizer(self, sent):      

 return list(sent)  

  def train(self):      

 for tag, doc in self.data:          

 words = self._tokenizer(doc)            

 for word in words:                

self.tags[tag] += 1                

self.tagwords[(tag, word)] += 1              

 self.total += 1    

def predict(self, inp):        

words = self._tokenizer(inp)        

tmp = {}      

 for tag in self.tags.keys():          

 tmp[tag] = math.log(self.tags[tag]) -  math.log(self.total)            

for word in words:                

tmp[tag] += math.log(self.tagwords.get((tag, word), 1.0)) - math.log(self.tags[tag])      

 ret, score = 0, 0.0      

 for t in self.tags.keys():            

cnt = 0.0          

 for tt in self.tags.keys():                

cnt += math.exp(tmp[tt] - tmp[t])          

 cnt = 1.0 / cnt          

 if cnt > score:              

 ret, score = t, cnt        

return ret
import pandas as pd

mydata = pd.DataFrame(pd.read_csv('F:/BDCI/train/train.csv'))

mydata = mydata[['content','sentiment_value']]

train = []for i in range(len(mydata)):  

 train.append((mydata.iloc[i]['sentiment_value'], mydata.iloc[i]['content']))

train
SVM：

支持向量机（Support Vector Machine）是一种二类分类模型。他的基本模型是定义在特征空间上的间隔最大的线性分类器，此外如果使用了核技巧之后还可以称为非线性分类器。当一个分类问题，数据是线性可分的，也就是用一根棍就可以将两种小球分开的时候，我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可，寻找这个最大间隔的过程，就叫做最优化。

import numpy as np
import sklearn
from sklearn.datasets import fetch_20newsgroups
twenty_train=fetch_20newsgroups(subset='train',shuffle=True)
twenty_train.traget_names
from sklearn.feature_extraction.text import CountVectorizer
count_vect=CountVectorizer()
x_train_counts=count_vect.fit_transform(twenty_train.data)#词袋模型
from sklearn.naive_bayes import MultinomialNB
clf=MultionmialNB.fit(x_train_counts,twenty_train.target)
twenty_test=fetch_20newsgroups(subset='test',shuffle=True)#生成测试集
x_test_counts=count_vect.transform(twenty_test.data)
predicted=clf.predict(x_test_counts)
np.mean(predicted==twenty_test.target)
 

LDA:

LDA（Latent Dirichlet Allocation）是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。
LDA是一种非监督机器学习技术，可以用来识别大规模文档集（document collection）或语料库（corpus）中潜藏的主题信息。它采用了词袋（bag of words）的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序，这简化了问题的复杂性，同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。
对于语料库中的每篇文档，LDA定义了如下生成过程（generativeprocess）：  
(1)对每一篇文档，从主题分布中抽取一个主题;
(2)从上述被抽到的主题所对应的单词分布中抽取一个单词;
(3)重复上述过程直至遍历文档中的每一个单词。  
语料库中的每一篇文档与T（通过反复试验等方法事先给定）个主题的一个多项分布 （multinomialdistribution）相对应，将该多项分布记为θ。每个主题又与词汇表（vocabulary）中的V个单词的一个多项分布相对应，将这个多项分布记为φ。

公式：p(w|d)=p(w|t)*p(t|d)  

代码：

from gensim.test.utils import common_texts
from gensim.corpora.dictionary import Dictionary

# Create a corpus from a list of texts
common_dictionary = Dictionary(common_texts)
common_corpus = [common_dictionary.doc2bow(text) for text in common_texts]

# Train the model on the corpus.
lda = LdaModel(common_corpus, num_topics=10)
from gensim.corpora import Dictionary
dct = Dictionary(["máma mele maso".split(), "ema má máma".split()])
dct.doc2bow(["this", "is", "máma"])
[(2, 1)]
dct.doc2bow(["this", "is", "máma"], return_missing=True)
([(2, 1)], {u'this': 1, u'is': 1})
from gensim.models import LdaModel

lda = LdaModel(common_corpus, num_topics=10)

lda.print_topic(1, topn=2)

'0.500*"9" + 0.045*"10"