难度:容易
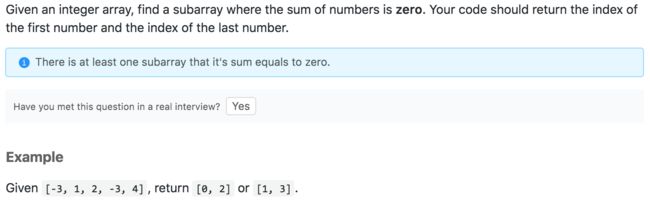
1. Description
2. Solution
- python
暴力方法,时间复杂度O(n^2)
class Solution:
"""
@param nums: A list of integers
@return: A list of integers includes the index of the first number and the index of the last number
"""
def subarraySum(self, nums):
# write your code here
for i in range(len(nums)):
m_sum = 0
for j in range(i,len(nums)):
m_sum += nums[j]
if(m_sum==0):
return [i,j]
用前缀和,时间复杂度O(n)
前缀和prefix_sum[i] = nums[0]+nums[1]+...nums[i],即数组前i项和。
利用nums[i+1]+nums[i+1]+...+nums[j] = prefix_sum[j]-prefix_sum[i],
当prefix_sum[j]=prefix_sum[i]时,i+1到j的子串和为0。
class Solution:
"""
@param nums: A list of integers
@return: A list of integers includes the index of the first number and the index of the last number
"""
def subarraySum(self, nums):
# write your code here
prefix_hash = {0:-1}
prefix_sum = 0
for i in range(len(nums)):
prefix_sum += nums[i]
if prefix_sum in prefix_hash.keys():
return prefix_hash[prefix_sum]+1,i
prefix_hash[prefix_sum] = i
return -1,-1
3. Reference
- https://www.lintcode.com/problem/subarray-sum/description