pytorch实现二分类（单隐藏层的神经网络）

同样是吴恩达深度学习课程的作业，我把它改成pytorch版本了。有了上次的经验，这次就没花多少时间了。

1 packages

import numpy as np
import torch
from torch import nn
import matplotlib.pyplot as plt
import torch.utils.data as Data
from torch.nn import init
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

%matplotlib inline

2 dataset

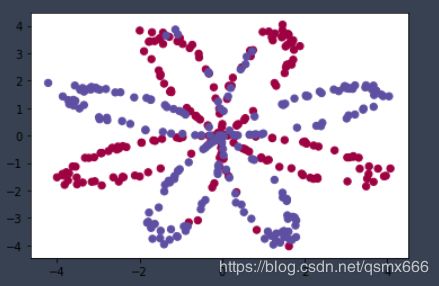
X, Y = load_planar_dataset()
# Visualize the data:
plt.scatter(X[0, :], X[1, :], c=Y[0, :], s=40, cmap=plt.cm.Spectral);

数据长这样：

X = torch.from_numpy(X.T).float()
Y = torch.from_numpy(Y.T).float()

shape_X = X.shape
shape_Y = Y.shape
m = X.shape[1]  # training set size

print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))

3 our model

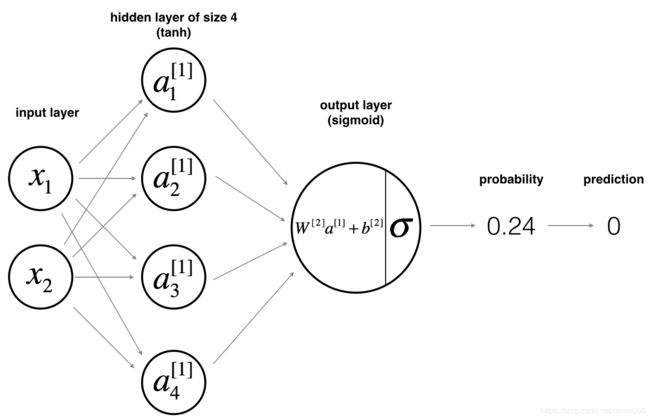
3.1 definition

num_inputs, num_hiddens, num_outputs = 2, 4, 1

class Classification(nn.Module):
    def __init__(self):
        super(Classification, self).__init__()
        self.hidden = nn.Linear(num_inputs, num_hiddens)
        self.tanh = nn.Tanh()
        self.output = nn.Linear(num_hiddens, num_outputs)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.hidden(x)
        x = self.tanh(x)
        x = self.output(x)
        x = self.sigmoid(x)
        return x
        
net = Classification()

3.2 initialize the parameters

init.normal_(net.hidden.weight, mean=0, std=0.01)
init.normal_(net.output.weight, mean=0, std=0.01)
init.constant_(net.hidden.bias, val=0)
init.constant_(net.output.bias, val=0)

3.3 define the loss function

loss = nn.BCELoss() 

3.4 define the optimizer

optimizer = torch.optim.SGD(net.parameters(), lr=1.2, momentum=0.9)

3.5 evaluate the accuracy

def evaluate_accuracy(x,y,net):
    out = net(x)
    correct= (out.ge(0.5) == y).sum().item()
    n = y.shape[0]
    return correct / n

3.6 train

def train(net,train_x,train_y,loss,num_epochs,optimizer=None):

    for epoch in range(num_epochs):
        out = net(train_x)
        l = loss(out, train_y)
        optimizer.zero_grad()
        l.backward()
        optimizer.step()
        train_loss = l.item()

        if (epoch + 1) % 100 == 0:
            train_acc = evaluate_accuracy(train_x,train_y, net)
            print('epoch %d ,loss %.4f'%(epoch + 1,train_loss)+', train acc {:.2f}%'
                  .format(train_acc*100))

num_epochs = 1000
train(net, X, Y, loss, num_epochs, optimizer)

3.7 output

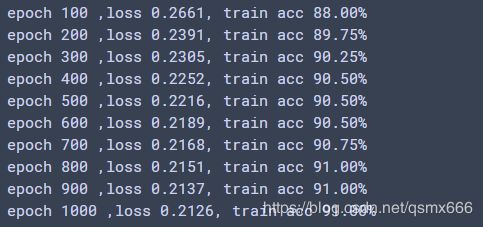
这是效果：

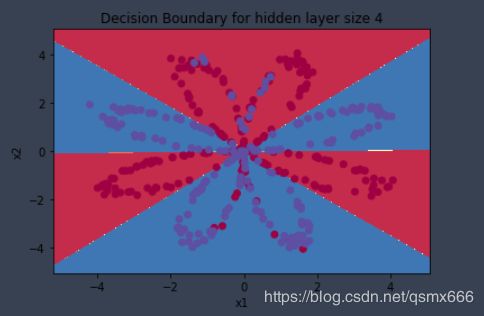
吴恩达课程作业中做了一个logistic 回归的对比。由于数据集不是线性可分的，所以效果并不好，准确率只有47%。而新模型由于加入了非线性因素（隐藏层tanh激活函数），所以能更好地拟合数据。

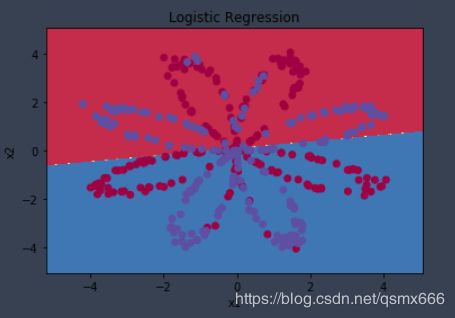
4 discussion about hidden layer size

模型中的隐藏单元数量是一个超参数。通过调整隐藏单元个数，我们可以发现在num_hiddens=5时效果最好，隐藏单元数量过大会导致过拟合。
num_hiddens=20时效果：