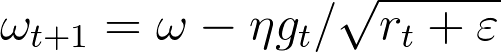2020李宏毅机器学习课程作业——Homework1：Linear Regression

一、作业获取途径

课程网址：http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html

B站视频地址：https://www.bilibili.com/video/BV1JE411g7XF?from=search&seid=18330864429491522852

如果不能访问课程网址，作业的压缩包如下，链接：https://pan.baidu.com/s/1PZZnWZKZONDCGTMznKINEg 
提取码：5of8

案例提供的是在Colab上运行的，不能使用的同学可以直接使用其他python编程工具即可。

二、作业说明

本次目標：由前 9 個小時的 18 個 features (包含 PM2.5)預測的 10 個小時的 PM2.5。

import sys
import pandas as pd
import numpy as np
#from google.colab import drive 
#!gdown --id '1wNKAxQ29G15kgpBy_asjTcZRRgmsCZRm' --output data.zip
#!unzip data.zip
# data = pd.read_csv('gdrive/My Drive/hw1-regression/train.csv', header = None, encoding = 'big5')
data = pd.read_csv('./train.csv', encoding = 'big5')
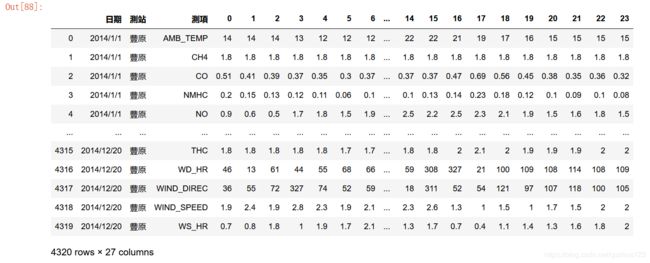
data

输出为：

数据说明：每行代表一个观测数据在24个时辰的值 故有效数据共24列，加上前三列标注，共27列；每天有18个观测数据类型，取每个月前20天的数据为训练集，每年12个月，共18*20*12=4320行。所以数据为4320*27.

获取有效数据，去除前三列，将降雨字符数字化：

# 丢弃前两列，需要的是从第三列开始的数值
data = data.iloc[:, 3:]
# 把降雨的NR字符变成数值0
data[data == 'NR'] = 0
# 把dataframe转换成numpy的数组
raw_data = data.to_numpy()
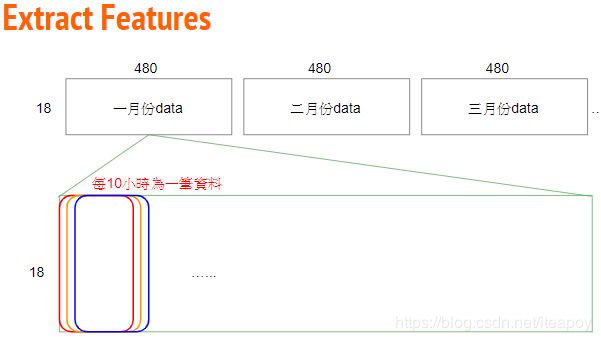
raw_data.shape

將原始 4320 * 18 的資料依照每個月分重組成 12 個 18 (features) * 480 (hours) 的資料。

month_data = {}
for month in range(12):
    sample = np.empty([18, 480])
    for day in range(20):
        sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
    month_data[month] = sample

 

每個月會有 480hrs，每 9 小時形成一個 data，每個月會有 471 個 data，故總資料數為 471 * 12 筆，而每筆 data 有 9 * 18 的 features (一小時 18 個 features * 9 小時)。

對應的 target 則有 471 * 12 個(第 10 個小時的 PM2.5)

x = np.empty([12 * 471, 18 * 9], dtype = float)
y = np.empty([12 * 471, 1], dtype = float)
for month in range(12):
    for day in range(20):
        for hour in range(24):
            if day == 19 and hour > 14:
                continue
            x[month * 471 + day * 24 + hour, :] = month_data[month][:,day * 24 + hour : day * 24 + hour + 9].reshape(1, -1) #vector dim:18*9 (9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9)
            y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9] #value
print(x)
print(y)

标准化：

mean_x = np.mean(x, axis = 0) #18 * 9 
std_x = np.std(x, axis = 0) #18 * 9 
for i in range(len(x)): #12 * 471
    for j in range(len(x[0])): #18 * 9 
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

 #Split Training Data Into "train_set" and "validation_set" 這部分是針對作業中 report 的第二題、第三題做的簡單示範，以生成比較中用來訓練的 train_set 和不會被放入訓練、只是用來驗證的 validation_set。

import math
x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8): , :]
y_validation = y[math.floor(len(y) * 0.8): , :]

训练： 

 

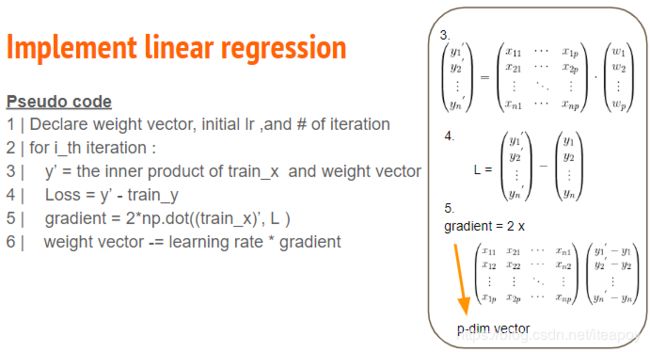
 Adagrad是一种动态调整学习率的算法。更新公式为：

                

其中gt代表偏导数值，η代表学习率，ϵ避免分母为零。

dim = 18 * 9 + 1
w = np.zeros([dim, 1])
x = np.concatenate((np.ones([12 * 471, 1]), x), axis = 1).astype(float)
learning_rate = 100
iter_time = 1000
adagrad = np.zeros([dim, 1])
eps = 0.0000000001
beta = 0.999
los=[]
for t in range(iter_time):
    loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2))/471/12)#rmse
    los.append(loss)
    if(t%100==0):
        print(str(t) + ":" + str(loss))
    gradient = 2 * np.dot(x.transpose(), np.dot(x, w) - y) #dim*1
    adagrad += gradient ** 2
    w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
print(str(t) + ":" + str(loss))
np.save('weight.npy', w)
w

 测试：

# 读入测试数据test.csv
testdata = pd.read_csv('./test.csv', header = None, encoding = 'big5')
# 丢弃前两列，需要的是从第3列开始的数据
test_data = testdata.iloc[:, 2:]
# 把降雨为NR字符变成数字0
test_data[test_data == 'NR'] = 0
# 将dataframe变成numpy数组
test_data = test_data.to_numpy()
# 将test数据也变成 240 个维度为 18 * 9 + 1 的数据。
test_x = np.empty([240, 18*9], dtype = float)
for i in range(240):
    test_x[i, :] = test_data[18 * i: 18* (i + 1), :].reshape(1, -1)
for i in range(len(test_x)):
    for j in range(len(test_x[0])):
        if std_x[j] != 0:
            test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
test_x = np.concatenate((np.ones([240, 1]), test_x), axis = 1).astype(float)

 载入模型：

w = np.load('weight.npy')
ans_y = np.dot(test_x, w)
ans_y

保存预测结果：

import csv
with open('submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ['id_' + str(i), ans_y[i][0]]
        csv_writer.writerow(row)
        print(row)

然后就可以去kaggle提交了。初始模型是以100为学习率，迭代1000次，分数如下：

前面为Private  Score，后面为Public Score。此时的损失为7.09左右，1000次毕竟比较少，换成10000次后，从6000次开始损失收敛至5.68左右，说明已经找到最优。同样为10000次，学习率换成更小的对结果并无影响，所以Adagrad已经收敛。提交结果如下：

可以看到分数均有提升。 

优化算法改成Adam后，分数如下，效果稍差一些。

换成RMSprop后，分述如下，效果比Adam好点但比adagrad稍差。

 

综合来看，三者效果差距不大，损失函数均可收敛至5.68左右。

写在最后：

我是一个刚接触机器学习不久的小白，借着写博客来记录一下学习历程并加深理解，文中难免有错误，若您读后发现有错误，望不吝赐教，谢谢。