李宏毅机器学习HW1之PM2.5预测MATLAB实现,两个参数计算

李宏毅机器学习HW1之PM2.5预测MATLAB实现,两个参数计算

前9小时数据预测多参数计算在我下篇博客
学习了李宏毅的机器学习，深入浅出特别适合入门，在网上搜集关于其作业的解答基本没有教程，我也是新手，尽量保持作业的更新，希望互相交流。

作业简述

作业视频介绍点击这里是B站的视频，转载至YouTube李宏毅专栏
作业需要下载，原始数据和结果答案在GitHub中下载。
原始数据包括每天每小时的PM2.5值，温度等，如下图所示

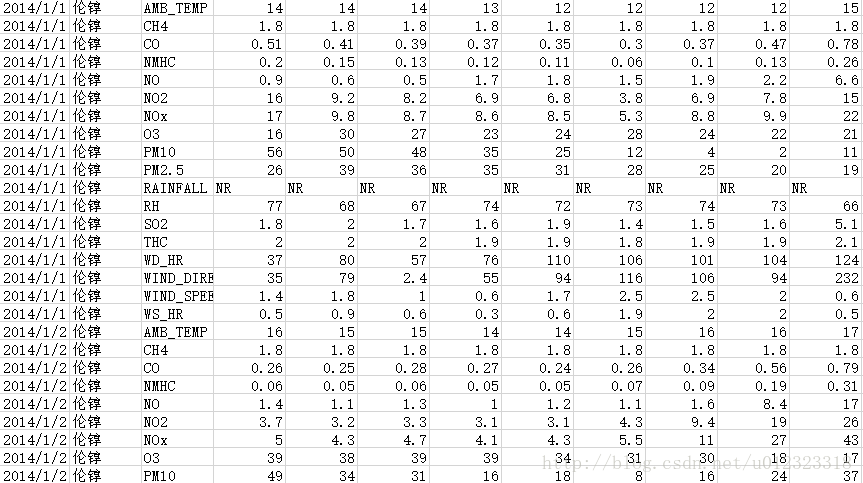
先将数据提取出来

做测试文件只提取PM2.5值，X1，X2是输出前两小时的PM2.5，Y（输出）是当前时间（或者说需要预测）的PM2.5

提取代码如下所示：

m=1;

X1=zeros(1,5280);
X2=zeros(1,5280);
Y=zeros(1,5280);%内存预分配，增加提取效率
size_one_row=length(csvread('train.csv',10,3,[10,3,10,24]));%表示CSV一行中数据量
for i=0:18:239*18
    X1(1,m:m+size_one_row-1)=csvread('train.csv',10+i,3,[10+i,3,10+i,24]);
    X2(1,m:m+size_one_row-1)=csvread('train.csv',10+i,4,[10+i,4,10+i,25]);
    Y(1,m:m+size_one_row-1)=csvread('train.csv',10+i,5,[10+i,5,10+i,26]);
    m=m+size_one_row;
end
clear m size_one_row i;

两个参数的gradient descend

设model为

y=b+w1+w2

设Loss Function

L(f)=L(w1,b)=∑(y^−(b+w1⋅x1+w2⋅x2))2

tips:这就是所谓的LMS算法
则可得

∂L∂b=∑2⋅[y^−(b+w1⋅x1+w2⋅x2)]⋅(−1)

∂L∂w1=∑2⋅[y^−(b+w1⋅xn1+w2⋅x2)]⋅(−x1)

∂L∂w1=∑2⋅[y^−(b+w1⋅xn1+w2⋅x2)]⋅(−x2)

则需要找到 w^1,w^2,b^ 使得Loss Function 取最小值

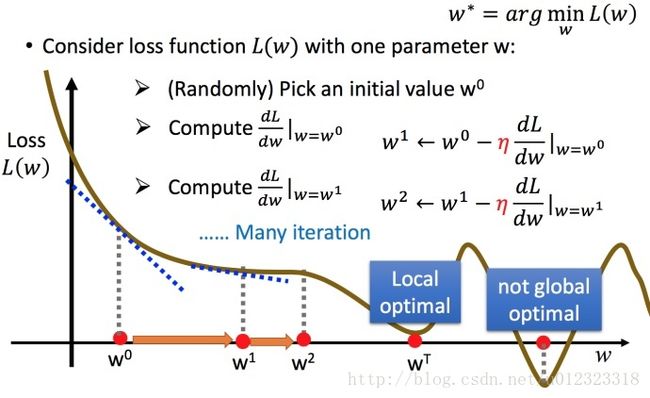
具体理论请看另一位博主的 文章这里不再重复这里主要是算法实现

先需要确定learning rate 和 iteration 推荐阅读确定其值
代码如下：

%initial parameters
b=5;
w1=1;
w2=1;
lr=0.00000001;
iteration=25;

figure(1);%显示Loss Function 收敛速度
hold on

for i=0:iteration
    if(i>=1)
        scatter(i,LossFun,'r');
    end
    LossFun=0;

    b_grad=0;
    w1_grad=0;
    w2_grad=0;
    for n=1:length(Y)
        b_grad=b_grad - 2*( Y(n)- (b+w1*X1(n)+ w2*X2(n) ) );
        w1_grad=w1_grad - 2*X1(n)*(Y(n)- (b+w1*X1(n)+ w2*X2(n) ) ); 
        w2_grad=w2_grad - 2*X2(n)*(Y(n)- (b+w1*X1(n)+ w2*X2(n) ) );
        LossFun=LossFun+( Y(n)- (b+w1*X1(n)+w2*X2(n)) )^2;%求Loss Function的值
    end
        b= b-lr*b_grad;
        w1= w1-lr*w1_grad;
        w2= w2-lr*w2_grad;
end
hold off

显示Loss Funtion 收敛如下
在 learning rate 取10E-8时收敛如下图所示

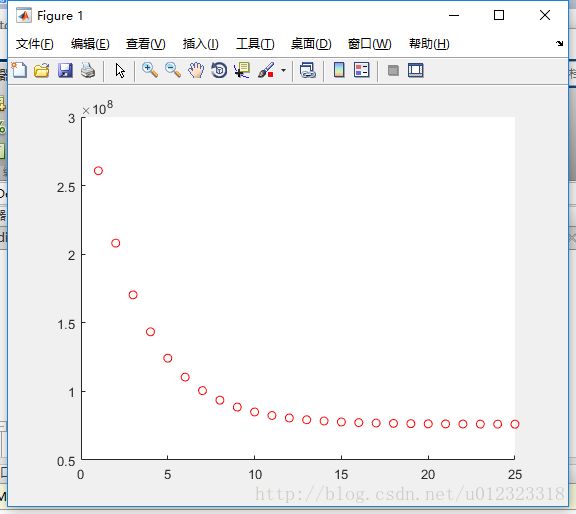
若取lr=1.5E-7 Loss Funtion 发散

大概可知lr不能超过10E-7

不做任何修正，固定学习速率，进行gradient descend

选择lr为 10E-7 选择学习周期为150000，同时当每个值的偏导数小于10E-5时认为，到达最佳 b,w1,w2
对上求取lr的函数稍加修改即可得到MATLAB程序，如下

%initial parameters
b=1;
w1=1;
w2=1;
lr=0.0000001;
iteration=150000;

for i=0:iteration   
    b_grad=0;
    w1_grad=0;
    w2_grad=0;
    for n=1:length(Y)
        b_grad=b_grad - 2*( Y(n)- (b+w1*X1(n)+ w2*X2(n) ) );
        w1_grad=w1_grad - 2*X1(n)*(Y(n)- (b+w1*X1(n)+ w2*X2(n) ) ); 
        w2_grad=w2_grad - 2*X2(n)*(Y(n)- (b+w1*X1(n)+ w2*X2(n) ) );
    end
        b= b-lr*b_grad;
        w1= w1-lr*w1_grad;
        w2= w2-lr*w2_grad;
        if(abs(b_grad)<10e-5&&abs(w1_grad)<10e-5&&abs(w2_grad)<10e-5) %在导数小于10E-5时认为到达最小值
            break;
        end
end

通过测试，需要进行45449次学习到达最佳值，并且计算时间为41.212 s