逻辑(斯谛)回归（Logistic Regression）

GitHub
简书
CSDN

在我们学习机器学习的过程中，我们所需解决的问题，大致可以分为两部分：分类和回归.其中,分类是指模型用来预测一个有限的离散值集合中的一个，比如猫狗分类，肿瘤的恶性或良性; 回归是指模型的输出是一个连续变量，比如预测房价、身高等.本篇内容讲解的是机器学习中经典的逻辑(斯谛)回归（Logistic Regression)，从名字上看，大家误以为该方法是一种回归方法，其实不然，它是分类方法的一种，常用于二元分类，但是为什么会取名回归，我个人理解大致有如下几点原因：

1. 利用回归的思想来解决分类问题;
2. 它的输出也是一个连续值，通过设定阈值来实现分类 

1. 逻辑斯谛分布

定义：设X是连续随机变量，X服从逻辑斯谛分布是指X具有下列分布函数和密度函数：

$$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-u)/\gamma }}\text{\hspace{1em}(1)}$$

$$f(x)=F^{{}^{\prime }}(x)=\frac{e^{-(x-\mu )\gamma }}{\gamma (1+e^{-(x-u)/\gamma }{)}^2}\text{\hspace{1em}(2)}$$

其中,$\mu$为位置参数,$\gamma >0$为形状参数.

该函数以点$(\mu ,\frac{1}{2})$为中对称，既有如下关系：
$$\begin{array}{rl}F(-x+\mu )& =1-F(x+\mu )\\ F(-x+\mu )-\frac{1}{2}& =F(x+\mu )+\frac{1}{2}\end{array}\text{\hspace{1em}(3)}$$
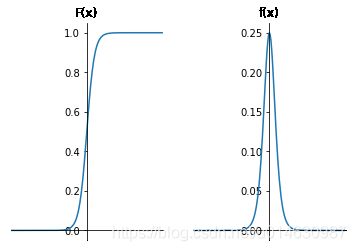
形状参数$\gamma$的值越小，曲线在中心附近增长的越快.该函数的图形如下图所示：

图一 逻辑斯谛分布的分布函数和密度函数

2 二元逻辑斯谛回归

二元逻辑斯谛回归模型是一种分类模型，有条件概率分布$P(Y|X)$表示，X取值为实数，随机变量 Y 取值为 1或0；

逻辑斯谛回归模型的条件概率如下：

$$\begin{array}{rl}p(Y=1|x)& =\frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}=\frac{1}{1+exp(-(w\cdot x+b))}\\ P(Y=0|x)& =\frac{1}{1+exp((w\cdot x+b))}\end{array}\text{\hspace{1em}(4)}$$

这里, $ x \in R^n $表示样本的特征向量，$Y \in {0, 1}$是输出表示样本的类别, $w\in R^n$ 和 $ b \in R$是模型的参数，其中，$w$ 表示权重向量,$b$表示偏置。$w\cdot x$表示$w$和$x$的内积.通常为了方便，我们将样本和权重向量进行扩充，仍记作$w$和$b$：
$$w=(w^1,w^2...w^n,b)$$
$$x=(x^1,x^2...x^n,1)$$

此时逻辑斯蒂回归模型记作:

$$\begin{array}{rl}p(Y=1|x)& =\frac{exp(w\cdot x)}{1+exp(w\cdot x)}\\ P(Y=0|x)& =\frac{1}{1+exp((w\cdot x))}\end{array}\text{\hspace{1em}(5)}$$

几率是指一个事件发生与不发生的概率比值,即$\frac{p}{1-p}$
则它的对数几率为$lnit(p)=log\frac{p}{1-p}$,对于逻辑斯蒂回归回归而言，其对数几率为
$$logit(\frac{P(Y=1|x)}{1-P(Y=1|x)})=w\cdot x\text{\hspace{1em}(6)}$$

3 模型参数估计

对于给定的训练数据集$T=\{(x_1,y_1),(x_2,y_2)...(x_n,y_x)\}$,可以应用极大似然估计(使模型预测的标签为真是标签的值最大化)模型参数，从而得到最优的逻辑斯蒂回归模型。

首先，设$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$,则似然函数为:
$$\begin{array}{r}\prod _{i=1}^n[\pi (x){]}^{y_i}[1-\pi (x){]}^{1-y_i}=\prod _{i=1}^n{y}_i\pi (x_i)+(1-y_i)(i-\pi (x_i))\end{array}\text{\hspace{1em}(7)}$$
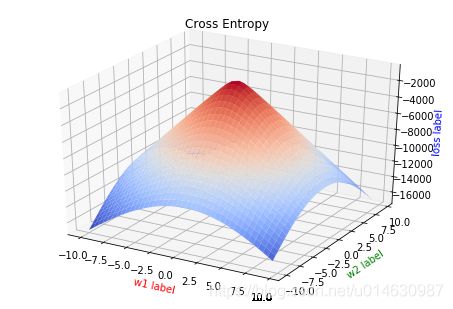
极大似然函数和交叉熵的树学公式形式时一摸一样的，但是他们背后的数学原理略有不同。
通常在处理优化问题时，我们都利用对数函数来把连乘变成求和来简化问题，因此公式七的对数似然函数为：
$$\begin{array}{rl}L(w)& =\sum _{i=1}^n[y_{i}ln\pi (x_i)+(1-y_i)ln(1-\pi (x_i))]\\ & =\sum _{i=1}^n[y_{i}ln\pi (x_i)-y_{i}ln(1-\pi (x_i))+ln(1-\pi (x_i))]\\ & =\sum _{i=1}^n[y_{i}ln\frac{\pi (x_i)}{1-\pi (x_i)}(注：这就是对数几率值）+ln(1-\pi (x_i))]\\ & =\sum _{i=1}^n[y_i(w\ast x_i)+ln(\frac{1}{1+exp((w\cdot x))})]\\ & =\sum _{i=1}^n[y_i(w\ast x_i)-ln(1+exp(w\cdot x_1))]\end{array}\text{\hspace{1em}(8)}$$

通过梯度下降和拟牛顿法即可求的该函数，我们求$L(w)$对$w$的倒数:

$$\begin{array}{rl}\frac{\partial L(w)}{\partial w}& =\sum _{i=1}^n[y_i{x}_i-(\frac{1}{1+exp(w\cdot x_1)}\ast exp(w\cdot x_i))\ast x_i]\\ & =\sum _{i=1}^n[y_i{x}_i-\pi (x_i)\ast x_i]\end{array}\text{\hspace{1em}(9)}$$

通常我们在实际优化的时候，都是求取最小值，因此通常使用$-L(w)$作为损失函数.

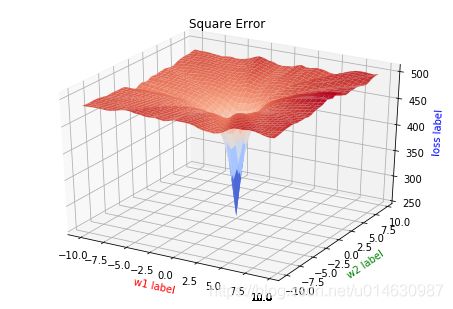
问题:在机器学习或深度学习中,我们通常以$L_2$作为损失函数，但是为什么这里是用了极大似然估计？

我们先观察一下使用$L_2$范数作为损失函数时，对$w$的求导公式:
$$\begin{array}{rl}{L}_2(w)& =\frac{1}{2}\sum _{i=1}^n(\pi (x_i)-y_i{)}^2\\ \frac{\partial l_2(w)}{\partial w}& =\sum _{i=1}^n[(\pi (x_i)-y_i)\ast \frac{\partial \pi (x_i)}{\partial z}\ast \frac{\partial z}{\partial w}]\\ & =\sum _{i=1}^n[(\pi (x_i)-y_i)\pi (x_i)(1-\pi (x_i))x_i]\end{array}\text{\hspace{1em}(10)}$$

其中, $z=w\cdot x$, 则$\pi (x)=\frac{exp(x)}{1+exp(x)}$,其导数为${\pi }^{{}^{\prime }}(x)=\pi (x)(1-\pi (x))$

这里主要考虑的是优化问题,极大似然估计函数是一个凸函数,这是优化问题再最容易优化的模型，我们可以得到全局最优解，而对于$L_2$，由于Sigmoig函数导数的特性，当$\pi (x)$接近0或者1时，此时的倒数就接近0，从而容易使函数陷入局部最优.

下图是两个损失函数以w为参数的简化图