matlab蚁群算法（ACA）详解（二）旅行商问题（TSP）详解

之前已经使用遗传算法、模拟退火算法是实现了对于TSP问题求解。本次主要使用的是蚁群算法进行求解，算法的基本原理已经在第一篇算法入门中做了详细的讲解。下面主要就是进行代码的实现：

数据使用测试数据如下：

	徐州	常州	青岛	北京	祁县	洛阳	黄山	武汉	西安	九江	舟山
徐州	0	471	410	392	399.5	412	449	348	335	517	600
常州	62	0	490	433	458.5	503	423	414	445	600	574
青岛	70	559	0	418	313.5	503	535	627	445	740	810
北京	99	549	465	0	382	431	532	459	430	575	792
祁县	111.5	579.5	365.5	387	0	472	517	390	321	581.5	646.5
洛阳	34	534	465	346	382	0	468	373	308	492	609
黄山	99	482	525	475	455	496	0	440	419	475	527
武汉	39	514	658	443	369	442	481	0	411	500	541
西安	55	574	505	443	329	406	489	440	0	511	654
九江	87	579	650	438	439.5	440	395	379	361	0	554
舟山	140	523	690	625	474.5	527	417	390	474	524	0

 

clear all
clc
%程序开始运行时开始计时
t0 = clock;
%载入数据
citys = xlsread('C:\Users\Administrator\Desktop\算法\ACA\Ch9_spots_data.xlsx','B2:L12');
%
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      %设定的对角矩阵修正值
        end
    end    
end

%初始化参数
m = 31;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
vol = 0.2;                           % 信息素挥发因子
Q = 10;                              % 常系数
Heu_F = 1./D;                        % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 100;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  
Limit_iter = 0;                      % 程序收敛时迭代次数

%迭代是使用ACA寻找最优解
while iter <= iter_max
    %随机分布蚂蚁的初始城市
    start = zeros(m,1);
    for i = 1:m
        temp = randperm(n);
        start(i) = temp(1);
    end
    Table(:,1) = start;
    
    %构造解空间
    citys_index = 1:n;
    
    %逐个蚂蚁选择路径
    for i = 1:m
        % 逐个城市路径选择
        for j = 2:n
            tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
            allow_index = ~ismember(citys_index,tabu);    %ismember根据一个变量的元素是否在另一个变量返回0-1矩阵
            allow = citys_index(allow_index);  % 待访问的城市集合
            P = allow;
            % 计算城市间转移概率
            for k = 1:length(allow)
                P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta;
            end
            P = P/sum(P);
            % 轮盘赌法选择下一个访问城市
            Pc = cumsum(P); 
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
    end
    
          % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
          Limit_iter = 1; 
          
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
              Limit_iter = iter; 
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-vol) * Tau + Delta_Tau;  
    
    iter = iter + 1;%迭代次数加一
    Table = zeros(m,n);%清空本次的路径表
end

% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
Time_Cost=etime(clock,t0);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
disp(['收敛迭代次数:' num2str(Limit_iter)]);
disp(['程序执行时间:' num2str(Time_Cost) '秒']);

% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...  %三点省略符为Matlab续行符
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
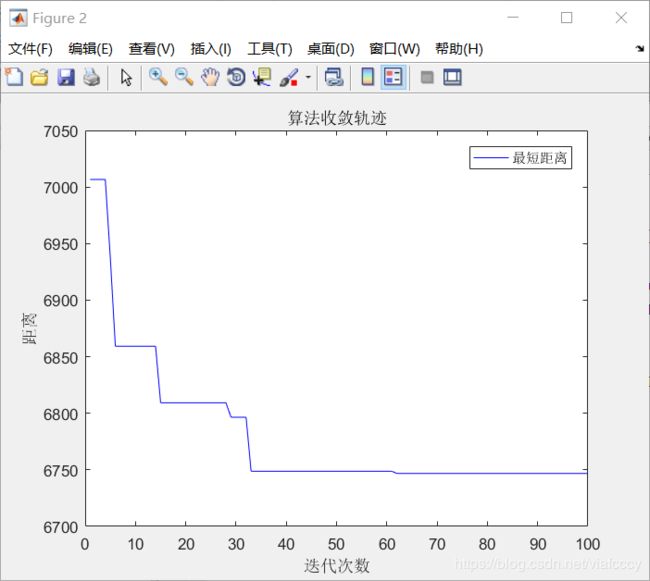
plot(1:iter_max,Length_best,'b')
legend('最短距离')
xlabel('迭代次数')
ylabel('距离')
title('算法收敛轨迹')

算法结果：

最短距离:6746.8159
最短路径:11   8  10   9   5   3   4   6   1   2   7  11
收敛迭代次数:62
程序执行时间:1.434秒