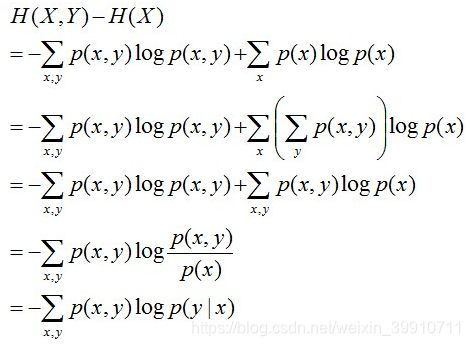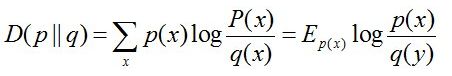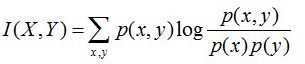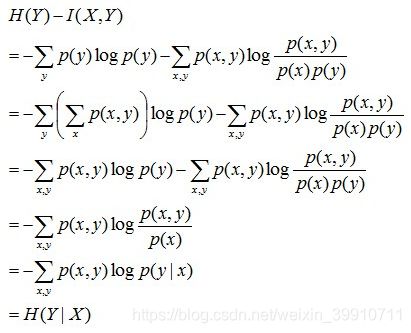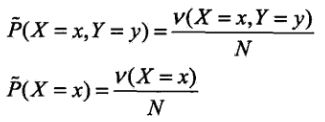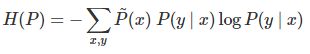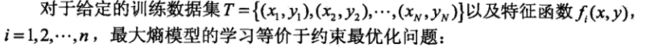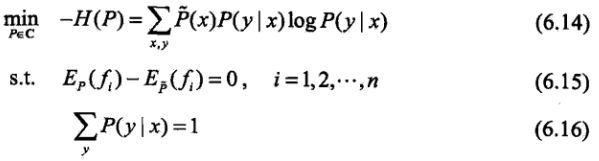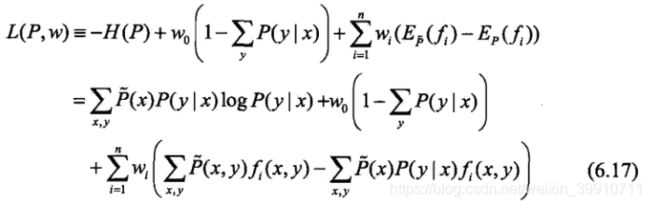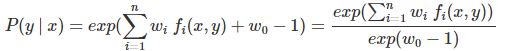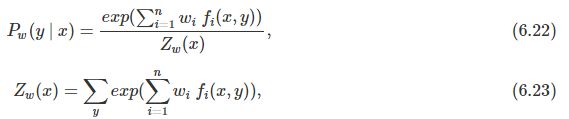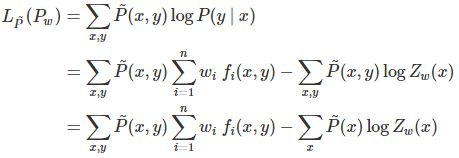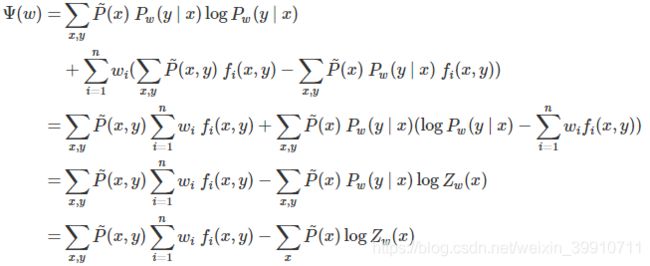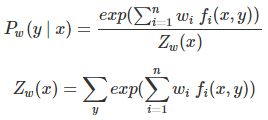机器学习算法（十九）：最大熵模型

目录

1 熵

1.1 熵的引入

1.2 熵的定义

2 最大熵模型

2.1 最大熵原理

2.2 最大熵模型

---

1 熵

详见：熵 https://blog.csdn.net/weixin_39910711/article/details/101299441

    熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度。在信息论里面，熵是对不确定性的测量。

1.1 熵的引入

    事实上，熵的英文原文为entropy，最初由德国物理学家鲁道夫·克劳修斯提出，其表达式为：

           

    它表示一个系系统在不受外部干扰时，其内部最稳定的状态。后来一中国学者翻译entropy时，考虑到entropy是能量Q跟温度T的商，且跟火有关，便把entropy形象的翻译成“熵”。

    我们知道，任何粒子的常态都是随机运动，也就是"无序运动"，如果让粒子呈现"有序化"，必须耗费能量。所以，温度（热能）可以被看作"有序化"的一种度量，而"熵"可以看作是"无序化"的度量。

    如果没有外部能量输入，封闭系统趋向越来越混乱（熵越来越大）。比如，如果房间无人打扫，不可能越来越干净（有序化），只可能越来越乱（无序化）。而要让一个系统变得更有序，必须有外部能量的输入。

    1948年，香农Claude E. Shannon引入信息（熵），将其定义为离散随机事件的出现概率。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。所以说，信息熵可以被认为是系统有序化程度的一个度量。
    若无特别指出，下文中所有提到的熵均为信息熵。

1.2 熵的定义

    下面分别给出熵、联合熵、条件熵、相对熵、互信息的定义。

    （1）熵：如果一个随机变量X的可能取值为X = {x1, x2,…, xk}，其概率分布为P(X = xi) = pi（i = 1,2, ..., n），则随机变量X的熵定义为：

        

    把最前面的负号放到最后，便成了：

          

    上面两个熵的公式，无论用哪个都行，而且两者等价，一个意思（这两个公式在下文中都会用到）。

    （2）联合熵：两个随机变量X，Y的联合分布，可以形成联合熵Joint Entropy，用H(X,Y)表示。
    （3）条件熵：在随机变量X发生的前提下，随机变量Y发生所新带来的熵定义为Y的条件熵，用H(Y|X)表示，用来衡量在已知随机变量X的条件下随机变量Y的不确定性。

    且有此式子成立：H(Y|X) = H(X,Y) – H(X)，整个式子表示(X,Y)发生所包含的熵减去X单独发生包含的熵。至于怎么得来的请看推导：

     

    简单解释下上面的推导过程。整个式子共6行，其中

• 第二行推到第三行的依据是边缘分布p(x)等于联合分布p(x,y)的和；
• 第三行推到第四行的依据是把公因子logp(x)乘进去，然后把x,y写在一起；
• 第四行推到第五行的依据是：因为两个sigma都有p(x,y)，故提取公因子p(x,y)放到外边，然后把里边的-（log p(x,y) - log p(x)）写成- log (p(x,y)/p(x) ) ；
• 第五行推到第六行的依据是：条件概率的定义p(x,y) = p(x) * p(y|x)，故p(x,y) / p(x) =  p(y|x)。

    （4）相对熵：又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布，则p对q的相对熵是：

              

     在一定程度上，相对熵可以度量两个随机变量的“距离”，且有D(p||q) ≠D(q||p)。另外，值得一提的是，D(p||q)是必然大于等于0的。

    （5）互信息：两个随机变量X，Y的互信息定义为X，Y的联合分布和各自独立分布乘积的相对熵，用I(X,Y)表示：

          

    且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。下面，咱们来计算下H(Y)-I(X,Y)的结果，如下：

        

      通过上面的计算过程，我们发现竟然有H(Y)-I(X,Y) = H(Y|X)。故通过条件熵的定义，有：H(Y|X) = H(X,Y) - H(X)，而根据互信息定义展开得到H(Y|X) = H(Y) - I(X,Y)，把前者跟后者结合起来，便有I(X,Y)= H(X) + H(Y) - H(X,Y)，此结论被多数文献作为互信息的定义。

2 最大熵模型

2.1 最大熵原理

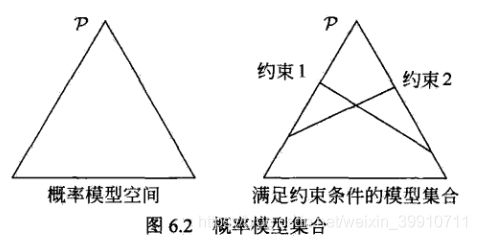
    熵的概念在统计学习与机器学习中真是很重要 。今天的主题是最大熵模型（Maximum Entropy Model，以下简称MaxEnt），MaxEnt 是概率模型学习中一个准则，其思想为：在学习概率模型时，所有可能的模型中熵最大的模型是最好的模型；若概率模型需要满足一些约束，则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。

    最大熵原理指出，对一个随机事件的概率分布进行预测时，预测应当满足全部已知的约束，而对未知的情况不要做任何主观假设。在这种情况下，概率分布最均匀，预测的风险最小，因此得到的概率分布的熵是最大。

        最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分是“等可能的”，等概率表示了对事实的无知。因为没有更多信息，这种判断是合理的，“等可能”不易操作，可通过“熵最大”来表示。

        一个简单的例子介绍最大熵原理：

2.2 最大熵模型

        最大熵原理是统计学习的一般原理，将它应用到分类得到最大熵模型。

    给定训练数据，可以确定联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布，分别以和表示

          

     其中v(X=x,Y=y)表示训练数据中样本(x,y)出现的频数，v(X=x)表示训练数据中输入x出现的频数，N表示训练样本容量。

    用特征函数f(x,y)描述x和y之间的某一事实，它是一个二值函数（一般地，特征函数可以是任意实值函数）。

      

    特征函数f(x,y)关于经验分布的期望值，用表示。

         

    特征函数f(x,y)关于模型P(Y | X)与经验分布的期望值，用表示。

         

    如果模型能够获取训练数据中的信息，那么就可以假设这里两个期望值相等，即

                                                 (2.1)

    或

                                                 (2.2)

    将式(2.1)或式(2.2)作为模型学习的约束条件，假如有n个特征函数，那么就有n个约束条件。

    最大熵模型的定义:
    假设满足所有约束条件的模型集合为：

          

    定义在条件概率分布P(Y | X)上的条件熵为：

           

    则模型集合C中条件熵H(P)最大的模型称为最大熵模型。式中的对数为自然对数。

2.3 最大熵模型的学习

          

    按照最优化问题的习惯，将求最大值问题改写为等价的求最小值问题：

           

          

         

    最优化的原始问题为：

           

    对偶问题是：

            

    由于拉格朗日函数 L(P,w) 是 P 的凸函数，原始问题(6.18)的解与对偶问题(6.19)的解是等价的。这样，可以通过求解对偶问题(6.19)来求解原始问题(6.18)。

    首先求解对偶问题(6.19)内部的极小化问题，得到的函数是 w 的函数，将其记作：

           

   Ψ(w)称为对偶函数，同时，将其解记作

          

    具体地，求 L(P,w) 对 P(y | x) 的偏导数，另偏导数等于0，解得

          

    由于，得

                   

    之后求解对偶问题(6.19)外部的极大化问题，将其解记为，即，可以应用最优化算法求解得到，代入得到，即学习到的最优模型（最大熵模型）。

2.4 极大似然估计

    从以上最大熵模型学习中可以看出，最大熵模型是由式(6.22)、式(6.23)表示的条件概率分布。下面证明对偶函数的极大化等价于最大熵模型的极大似然估计。

    已知训练数据的经验概率分布，条件概率分布的对数似然函数表示为

               

    当条件概率分布是最大熵模型(6.22)和(6.23)时，对数似然函数是最大熵模型(6.22)和(6.23)时，对数似然函数为：

                

    再看对偶函数Ψ(w)，由式(6.17)及式(6.20)可得

            

    可以发现，对偶函数等价于对数似然函数，证明最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计。

    这样，最大熵模型的学习问题转换为具体求解对数似然函数极大化或对偶函数极大化的问题。

               

    最大熵模型表现为以上形式，与logistic回归模型有类似的形式，它们又称对数线性模型。

 

 

https://www.cnblogs.com/liaohuiqiang/p/10979959.html