李宏毅ML作业1:预测PM2.5
在这里给出作业所需下载资料的链接
分析:
在线性回归的基础上预测PM2.5,首先根据自己的想法定义function set
预测N年N月N时的PM2.5,要求根据前九个小时所有数据来推测第十小时的PM2.5,这里认为第十小时(N)的PM2.5与前九个小时(N-1,N-2,…N-9)的PM2.5有关.
Y n = b + X p m 2.5 , n − 1 ∗ W n − 1 + . . . . + X p m 2.5 , n − 9 ∗ W n − 9 Y_n=b+X_{pm2.5,n-1}*W_{n-1}+....+X_{pm2.5,n-9}*W_{n-9} Yn=b+Xpm2.5,n−1∗Wn−1+....+Xpm2.5,n−9∗Wn−9
定义LossFunction
L = 1 n ∑ i = 1 n ( y − y ^ ) 2 L=\frac{1}{n}\sum_{i=1}^{n}(y-\hat{y})^2 L=n1i=1∑n(y−y^)2
过程
注意,下面用的是float类型计算
1.处理train.csv和test.csv文件
增加column名称并设为英文,改变编码
train data:
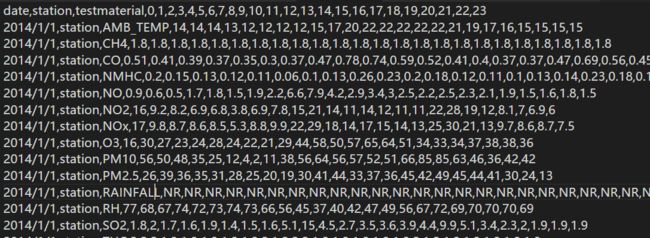
test data:
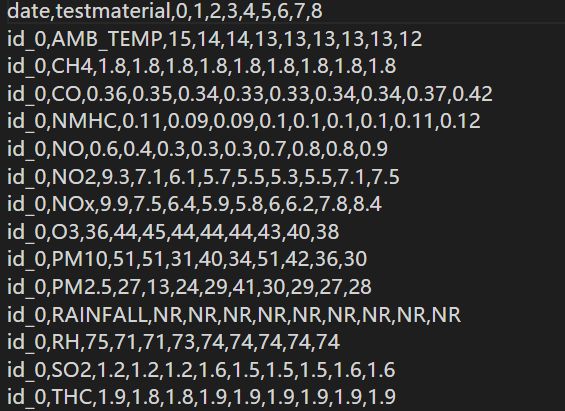
2.Parse train data to x,y
通过python中的pandas库对csv文件进行处理,取出关于PM2.5的数据,train data里一共有240天,每天可取15个连续9小时数据.则共有240x15=3600笔数据。
x:(3600,9)
相应的y:(3600,1)
import pandas as pd
import numpy as np
from pandas import DataFrame
import math
train=pd.read_csv("C:\\Project\\py\\airquality\\train.csv");
# pm=train[train[""]]
pm=train[train["testmaterial"]=="PM2.5"]
pm.drop(['date','station','testmaterial'],axis=1,inplace=True)
x=[]# 此时x,y为list
y=[]
for i in range(15):#冒号
temx=pm.iloc[:,i:i+9]
temx.columns=np.array(range(9))
temy=pm.iloc[:,i+9]
temy.columns=np.array(range(1))
x.append(temx)
y.append(temy)
x=pd.concat(x)#3600x9,3600=240x15,此时x为dataframe
y=pd.concat(y)#3600x1 ,y为serise
x=np.array(x,float)
y=np.array(y,float)
np.save("C:\\Project\\py\\airquality\\x.npy",x)
np.save("C:\\Project\\py\\airquality\\y.npy",y)
3.Train using gradient descent (adagrad)
利用梯度下降法进行训练得到最好的function.重点理解adagrad中一次微分除以二次微分的思想。
x=np.load("C:\\Project\\py\\airquality\\x.npy")
y=np.load("C:\\Project\\py\\airquality\\y.npy")
#adding baias
x = np.concatenate((np.ones((x.shape[0],1)),x), axis=1)
#init
w = np.zeros(len(x[0]))
l_rate = 10
repeat = 10000
s_grad=np.zeros(len(x[0]))
x_t=x.transpose()
# train
for i in range(repeat):
tem=np.dot(x,w)
loss=tem-y
grad=np.dot(x_t,loss)
s_grad+=grad**2
ada=np.sqrt(s_grad)
w=w-l_rate*grad/ada
np.save("C:\\Project\\py\\airquality\\model.npy",w)
4.Predict PM2.5 using model
利用上面生成的model对与test data中的数据进行预测,test data 中关于PM2.5数据共有240笔数据,即预测240笔数据。首先对test data进行处理和处理train data类似,充分利用了矩阵的乘法来代替计算偏微分,原理可以自行推导。
model=np.load("C:\\Project\\py\\airquality\\model.npy")
test=pd.read_csv("C:\\Project\\py\\airquality\\test.csv")
t=test[test["testmaterial"]=="PM2.5"]
t.drop(["date","testmaterial"],axis=1,inplace=True)
t=np.array(t,float)
t=np.concatenate((np.ones((t.shape[0],1)),t), axis=1)
res=[]
res=np.dot(t,w)
res
上面生成的结果res是list对象,可以自己再加以处理。
总结
首先自己还没有过多的深入探讨,以防误删先放上来,再上面的链接中可以查看正确的答案。
利用close form solution验证Model的正确性
尝试normalization