统计学习方法笔记(六)-非线性支持向量机原理及python实现
非线性支持向量机
- 非线性支持向量机
- 定义 非线性支持向量机
- 算法 非线性支持向量机学习算法
- 代码案例 TensorFlow
- 案例地址
非线性支持向量机
定义 非线性支持向量机
从非线性分类训练集,通过核函数与软间隔最大化,或凸二次规划,学习得到的分类决策函数
f ( x ) = sign ( ∑ i = 1 N α i ∗ y i K ( x , x i ) + b ∗ ) {f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} K\left(x, x_{i}\right)+b^{*}\right)} f(x)=sign(i=1∑Nαi∗yiK(x,xi)+b∗)
这个分类决策函数称为非线性支持向量机, K ( x , z ) K(x,z) K(x,z)是正定核函数
算法 非线性支持向量机学习算法
输入:训练集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},其中 X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , . . . , N \mathcal{X}=\mathcal{R}^{n},y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,...,N X=Rn,yi∈Y={−1,+1},i=1,2,...,N;
输出:分类决策函数
第一步:选取适当的核函数 K ( x , z ) K(x,z) K(x,z)和适当的参数 C C C,构造并求解最优化问题:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i ⋅ x j ) − ∑ i = 1 N α i \min _{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} αmin21i=1∑Nj=1∑NαiαjyiyjK(xi⋅xj)−i=1∑Nαi
s . t . ∑ i = 1 N α i y i = 0 s.t. \quad \sum_{i=1}^{N} \alpha_{i} y_{i}=0 s.t.i=1∑Nαiyi=0
0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N 0⩽αi⩽C,i=1,2,⋯,N
求得最优化问题的解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^{*}=(\alpha_{1}^{*},\alpha_{2}^{*}, \cdots,\alpha_{N}^{*})^{T} α∗=(α1∗,α2∗,⋯,αN∗)T
第二步:选择 α ∗ \alpha^{*} α∗的一个正分量 0 < α j ∗ < C 0< \alpha_{j}^{*}<C 0<αj∗<C,计算
b ∗ = y i − ∑ i = 1 N α i ∗ y i K ( x i , x j ) b^{*}=y_i-\sum_{i=1}^{N}\alpha_{i}^{*}y_i K(x_i,x_j) b∗=yi−i=1∑Nαi∗yiK(xi,xj)
第三步:构造决策函数
f ( x ) = sign ( ∑ i = 1 N α i ∗ y i K ( x i , x j ) ) f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*}y_i K(x_i,x_j)\right) f(x)=sign(i=1∑Nαi∗yiK(xi,xj))
注:当 K ( x , z ) K(x,z) K(x,z)是正定函数时,(1)、(2)、(3)是凸二次规划问题,存在解。
代码案例 TensorFlow
案例代码已上传:Github地址
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
sess = tf.Session()
第一步加载数据
# iris.数据 [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([[x[0], x[3]] for x in iris.data])
y_vals = np.array([1 if y==0 else -1 for y in iris.target])
class1_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==1]
class1_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==1]
class2_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1]
class2_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1]
第二步:声明模型变量并设置损失函数
# 批量大小
batch_size = 150
# 初始化占位符
x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
prediction_grid = tf.placeholder(shape=[None, 2], dtype=tf.float32)
# 创建变量
b = tf.Variable(tf.random_normal(shape=[1,batch_size]))
本案例采用高斯核函数,将低维空间数据转换为高维空间数据
K ( x , x ′ ) = e x p ( − γ ∣ ∣ x − x ′ ∣ ∣ 2 ) K(x, x')=exp\left(-\gamma|| x-x' ||^{2}\right) K(x,x′)=exp(−γ∣∣x−x′∣∣2)
损失函数:
− ( ∑ b − ∑ ( K ⋅ ∣ ∣ b ∣ ∣ 2 ∣ ∣ y ∣ ∣ 2 ) ) -\left(\sum\textbf{b} - \sum\left(K\cdot||\textbf{b}||^{2}||\textbf{y}||^{2}\right)\right) −(∑b−∑(K⋅∣∣b∣∣2∣∣y∣∣2))
# 高斯核函数 (RBF)
gamma = tf.constant(-50.0)
sq_vec = tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))
my_kernel = tf.exp(tf.multiply(gamma, tf.abs(sq_vec)))
# SVM模型的损失函数
first_term = tf.reduce_sum(b)
b_vec_cross = tf.matmul(tf.transpose(b), b)
y_target_cross = tf.matmul(y_target, tf.transpose(y_target))
second_term = tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)))
loss = tf.negative(tf.subtract(first_term, second_term))
声明预测时所采用的的核函数 RBF
rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),[-1,1])
rB = tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1),[-1,1])
pred_sq_dist = tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB))
pred_kernel = tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist)))
prediction_output = tf.matmul(tf.multiply(tf.transpose(y_target),b), pred_kernel)
prediction = tf.sign(prediction_output-tf.reduce_mean(prediction_output))
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32))
优化器设置
# 优化器的设置
my_opt = tf.train.GradientDescentOptimizer(0.01)
train_step = my_opt.minimize(loss)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
第三步:训练
# 开始训练
loss_vec = []
batch_accuracy = []
for i in range(300):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = x_vals[rand_index]
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
acc_temp = sess.run(accuracy, feed_dict={x_data: rand_x,
y_target: rand_y,
prediction_grid:rand_x})
batch_accuracy.append(acc_temp)
if (i+1)%75==0:
print('迭代次数#' + str(i+1))
print('损失 = ' + str(temp_loss))
# Create a mesh to plot points in
x_min, x_max = x_vals[:, 0].min() - 1, x_vals[:, 0].max() + 1
y_min, y_max = x_vals[:, 1].min() - 1, x_vals[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
grid_points = np.c_[xx.ravel(), yy.ravel()]
[grid_predictions] = sess.run(prediction, feed_dict={x_data: x_vals,
y_target: np.transpose([y_vals]),
prediction_grid: grid_points})
grid_predictions = grid_predictions.reshape(xx.shape)
%matplotlib inline
# Plot points and grid
plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8)
plt.plot(class1_x, class1_y, 'ro', label='I. setosa')
plt.plot(class2_x, class2_y, 'kx', label='Non setosa')
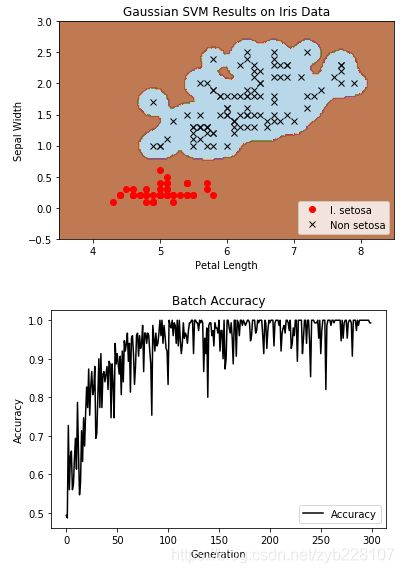
plt.title('Gaussian SVM Results on Iris Data')
plt.xlabel('Petal Length')
plt.ylabel('Sepal Width')
plt.legend(loc='lower right')
plt.ylim([-0.5, 3.0])
plt.xlim([3.5, 8.5])
plt.show()
# Plot batch accuracy
plt.plot(batch_accuracy, 'k-', label='Accuracy')
plt.title('Batch Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
案例地址
案例代码已上传:Github地址
参考资料:
[1] 《统计学习方法》
[2]: 《TensorFlow machine learning cookbook》
Github地址https://github.com/Vambooo/lihang-dl
更多技术干货在公众号:深度学习学研社
![]()