如何在音频分析中使用机器学习和深度学习
介绍
深度学习领域的学术论文很多都是关于计算机视觉和自然语言处理,而音频分析(包括自动语音识别,数字信号处理,音乐分类、标签、生成)领域的运用也逐渐受到了学者们的关注。目前最流行的机器学习系统,如虚拟助手 Alexa,Siri 和 Google Home,都是构建于音频信号提取模型之上。很多研究人员也在音频分类、语音识别、语音合成等任务上不断努力,构建了许多工具来分析、探索、理解音频数据。
这篇博客重点讨论数据科学家和AI工程师如何将机器学习和深度学习方法运用在音频分析领域中。为了理解模型是如何从数字音频信号中提取信息的,我们将深入介绍一些音频分析中所使用的核心特征工程方法。然后我们将使用 Librosa,一个非常优秀的Python 音频分析库,写一段简短的Python代码,在 UrbanSound8k数据集上训练一个神经网络。
音频中的机器学习:数字信号处理、滤波器组、梅尔-频率倒谱系数
通过构建机器学习模型来进行分类、描述或生成音频,通常会涉及到一些建模任务,这些任务的输入数据是音频样本。
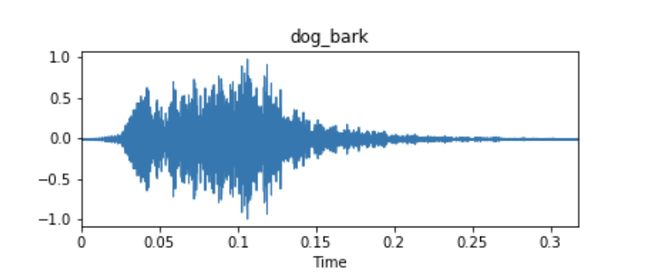
这些音频样本通常以时间序列的方式呈现,y-轴代表波形图的幅值。当麦克风或拾音器接受声音的时候,它周围的气压会产生变动,幅值就是这种变动值的函数。这些时间序列数据通常就用作为我们唯一的模型输入数据。
下面的10个例子均出自UrbanSound8k数据集,我们仅从肉眼去观测波形图,可能不会发现太多有用的信息。其中,发动机怠速、气笛、风炮的类别看上去非常相似。

梅尔-频率倒谱系数(MFCCs)由 Davis 和 Mermelstein 在1980年提出,是目前从音频波形图中提取信息的一个最佳特征。下面,我们将讨论MFCCs是如何产生的,以及为什么它们在音频分析中很管用。这一章节会比较技术性,所以在我们深入学习之前,我们要定义一些有关数字信号处理和音频分析的术语。此外,也列出了相关的维基百科和其他资源链接,帮助我们更好地去理解。
术语
采样和采样频率
在信号处理中,采样是将连续信号降为一组离散数值。采样频率是在一段固定时间中提取样本的数量。高采样频率会消耗更多的计算资源,但信息丢失的少,而低采样频率所需的计算资源较少,但是会丢失的信息较多。
幅值
声音波形的幅值是在一段时间内,波形变化的测量。另一个常用的幅值定义是,一个变量极值差异的振幅。
傅里叶变换
S T F T { x ( t ) } ( τ , ω ) = X ( τ , ω ) = ∫ − ∞ ∞ x ( t ) ω ( t − τ ) e − j ω t d t STFT\{x(t)\}(\tau, \omega) = X(\tau, \omega) = \int_{-\infty}^{\infty} x(t) \omega (t-\tau)e^{-j \omega t} dt STFT{x(t)}(τ,ω)=X(τ,ω)=∫−∞∞x(t)ω(t−τ)e−jωtdt
傅里叶变换能将一个时间(信号)的函数分解为不同的频率。这样,音乐和弦可以通过其构成音符的音量和频率来表示,一个函数的傅里叶变换可显示基础函数(信号)中每个频率的振幅(量)。
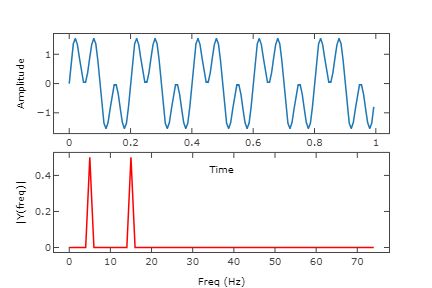
上图中,上面是一个数字信号;下面是该信号的傅里叶变换
傅里叶变换有多种变体,包括短时傅里叶变换,在Librosa库中有实现,将一个音频信号分割为不同的帧,然后计算每一帧的傅里叶变换。通常在音频处理中,傅里叶变换是一个非常管用而简洁的方法,将音频信号分解为构成频率。
周期图
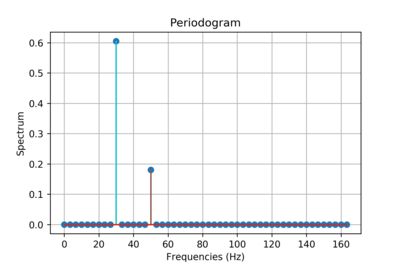
在信号处理中,周期图是对一个信号谱密度的估计。上面的周期图展示了两个正弦基函数的功率谱,频率分别是30 Hz 和 50 Hz。傅里叶变换的输出可以被看作为一个周期图。
谱密度

时间序列的功率谱是功率谱密度函数的简称,它定义为单位频带内的信号功率。它表示了信号功率随着频率的变化情况,即信号功率在频域的分布状况。功率谱表示了信号功率随着频率的变化关系。信号的统计平均值由频率含量来衡量,被称做为频谱。一个数字信号的谱密度表示了该信号的频率含量。
梅尔刻度
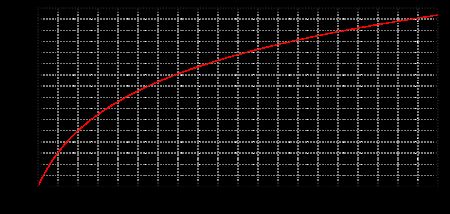
梅尔刻度是一种非线性刻度单位,表示人耳对等距音高变化的感官。其参考点定义是将 1000 H z 1000 Hz 1000Hz,且高于人耳听阈值40分贝以上的声音信号,定为 1000 m e l s 1000 mels 1000mels。在频率 500 H z 500 Hz 500Hz以上时,人耳每感觉到等量的音高变化,所需要的频率变化随频率增加而越来越大。这样的结果是,在赫兹刻度 500 H z 500 Hz 500Hz往上的四个八度(一个八度即为两倍的频率),只对应梅尔刻度上的两个八度。Mel的名字来源于单词melody,表示这个刻度是基于音高比较而创造的。梅尔刻度与线性的频率刻度赫兹(Hz)之间可以进行近似的数学换算。一种常用的将 f f f赫兹转换为 m m m梅尔的公式是:
m = 2595 log 10 ( 1 + f 700 ) m = 2595 \log_{10}(1+\frac{f}{700}) m=2595log10(1+700f)
倒频谱
倒频谱是将频谱的英文前四个字母反过来写,是信号频谱取对数的傅里叶变换后的新频谱(信号)。有时候为了计算的方便,将原来信号的频谱先转换为类似分贝的单位,再作逆傅里叶变换,把它视作一种新的信号做处理。
声谱图
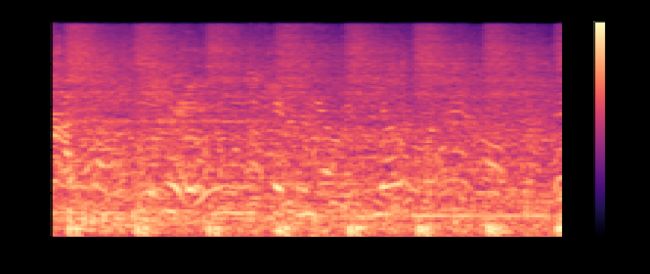
Urbansound8k数据集中一个音频样本的梅尔-频率声谱图
声谱图是一个信号频率频谱随着时间而变化的视觉呈现。想象频谱图的一种方法是将时间间隔数字信号上的周期图堆叠起来。
耳蜗
耳蜗是内耳的一个解剖结构,是外周听觉系统的组成部分,其核心部分是柯蒂氏器,为听觉传导器官,负责将来自中耳的声音信号转换为相应的神经电信号,交送脑的中枢听觉系统接受进一步处理,最终实现听觉知觉。
预处理音频:数字信号处理技术
数据集预处理、特征提取和特征工程是我们从基础数据中提取信息的几个步骤,这些信息在机器学习任务中,对于预测样本类别或某些目标变量的值很有用。在音频分析中,此过程主要基于查找音频信号的成分,以帮助我们将其与其他信号区分开。
MFCCs如之前所描述的,是从音频样本中提取信息的主流的工具。尽管有了像 Librosa 这样的库,我们仅需一行代码就可以计算出一个音频样本的 MFCCs,其背后的数学原理仍是比较复杂的。下面将一步步地介绍该原理。
计算某音频样本 MFCCs 的步骤:
- 将信号切成短帧;
- 对于每一帧,计算功率谱的周期图估计;
- 将梅尔滤波器组应用于功率谱,并对每个滤波器的能量求和;
- 计算对数滤波器组能量的离散余弦变换(DCT)。
1. 将信号切成短帧
将音频信号切成短帧很有用,因为它使我们可以将音频采样为离散的时间步长。我们假设在足够短的时间范围内音频信号不会改变。短帧持续时间的常用值在20-40ms之间。按照惯例,每帧要重叠10-15ms。
请注意,重叠帧使我们最终生成的特征高度相关。这就是为什么我们必须在所有这些操作结束时进行离散余弦变换。
2. 对于每一帧,计算功率谱的周期图估计
有了这些帧之后,我们需要计算每一帧的功率谱。时间序列的功率谱描述了功率在组成该信号的频率分量中的分布。根据傅立叶分析,任何物理信号都可以分解为多个离散频率或连续范围内的频谱。根据某信号的频率含量进行分析的统计平均值称为频谱。
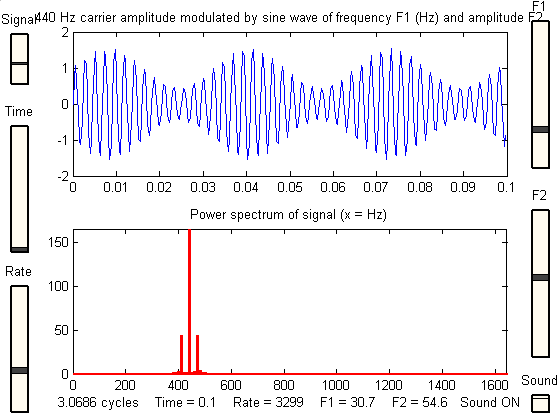
我们对每一帧都使用短时傅里叶变换来获取其功率谱。
3. 将梅尔滤波器组应用于功率谱,并对每个滤波器的能量求和
一旦有了我们的功率谱,我们仍然要做一些工作。人类的耳蜗不能很好地分辨相近的的频率,并且这种影响会随着频率的增加而变得更加明显。 Mel刻度是一种工具,使我们可以比线性频带更接近地估计人类听觉系统的响应。

从上面的图表中可以看到,梅尔滤波器随着频率的增加而变宽-我们不太关心较高频率下的变化。在低频下,滤波器会比较窄,人耳可以清楚地发觉差异,因此在我们的分析中,低频差异要更重要一些。
通过将傅立叶变换应用于输入数据而得到功率谱中的幅度,将这些幅度与三角形梅尔滤波器相关联,进行数据绑定。这种绑定很常用,这样子每个系数都乘以相应的滤波器增益,因此每个Mel滤波器都会保存一个表示该通道中频谱幅度的加权和。
一旦我们有了滤波器组能量,我们就可以取每个的对数。这一步是由于听觉的限制而导致的:人类不会感知音量的线性变化。要使感知到的声波音量增加一倍,声波的能量必须增加8倍。如果一个声波已经是高音量(高能量)了,则声波能量中较大的变化听起来可能也并没有多少不同。
4. 计算对数滤波器组能量的离散余弦变换(DCT)
因为我们的滤波器组能量是重叠的(请参见步骤1),所以它们之间通常存在很强的相关性。进行离散余弦变换可以帮助去除能量之间的相关性。值得庆幸的是,Librosa 的创建者已经抽象出了大量的这种数学运算,可以轻松地为您的音频数据生成MFCC。