线段数入门————单点修改+区间查询

1.什么是线段树：

线段树首先是一种二叉搜索树，为什么说是“线段”树呢？完全可以这么理解，即树中的每一个结点中存有一个区域（从起点到终点就好似线段一般），在下文中我将统一的将其称为该节点的管辖区域这样，我们就可以把线性的区域变为半线性的树。树有很多好处，比如说更改和查询操作的时间复杂度都是O(nodenum)，在频繁的查询修改的问题中线段树将会起到非常大的作用。

2.线段树的表示：

为了更好的说明这个问题，我画了一张图给出一个更为直观的印象（我刚开始接触线段树的时候，就是用的这种最笨最朴素的办法，抽象思维能力不够只能借助这样的工具来加深印象）。

说明：假设我们目前有10个数，存储在数组中：

A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] A[9] A[10]

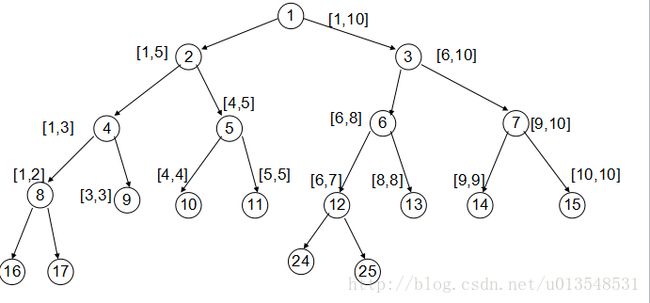
将该数组转化为线段树后，将会得到下图：

稍微解释一下，每一个结点里边的数字即该结点的编号，旁边的区间即该结点的管辖区间。

如tree[1]管辖的区间是[1,10]

很容易发现一个规律，即结点node的左儿子的标号是node*2,右儿子的标号是node*2+1.这里就是我们一个重要的构造原则。

3.构造线段树：

为此，我们先定义一个结构体类型。很明显，从上图来看，每一个结点需要表示它管辖的域，我们用变量left和right表示左右边界，除此之外，我们还会需要一些其他的域（例如某一个结点可以存取[left,right]之间的和、最值等)。

typedef struct{
	int data;
	int left,right;//[left,right] 
}Tree;

其中data可以根据具体的需要来进行更改。

这里，我们以求区间最值为例来给出建树的函数：

typedef struct{
	int max;
	int left,right;//[left,right] 
}Tree;

void Build(int index,int left,int right)
{
	
	tree[index].left = left;
	tree[index].right = right;
	
	if(left == right){
		tree[index].max = num[left];//这里的num[left]是指已经存在的数组，在所有数组读取完毕后建树 
		return ;
	}
	else{
		int mid = (left + right) >> 1;
		Build(index * 2,left,mid);
		Build(index * 2 + 1,mid + 1,right);
		tree[index].max = Max(tree[index*2].max,tree[index*2+1].max);
	}
};

这个函数十分的简单，开始的时候index = 1，即表示我们从线段树的第一个结点开始建树。

4.区间单点修改：

在很多事例中，我们可能会遇到要求改变某一个位置的数值，这就需要单点修改函数。可以说这是最最最基本的线段树修改函数。

同样以求最值为例，给出：

void Update(int root,int index,int value)//index是要修改的点的下标 
{
	if(tree[root].left == index && tree[root].right == index){
		tree[root].max = value;//当left == right == index时，即表明找到了要修改的位置 
		return ;
	}
	int mid = (tree[root].right + tree[root].left) >> 1;
	//mid是当前root结点所管辖区域的中间结点
	//我们要寻找的index无非两种情况，一种是在[left,mid]区间，另一种是在[mid+1,right]区间
	if(index <= mid)//在[left,mid]区间，查询左子树 
		Update(root*2,index,value);
	else if(mid < index)//在[mid+1,right]区间查询右子树 
		Update(root*2+1,index,value);
	tree[root].max = Max(tree[root*2].max,tree[root*2+1].max); 
};

单点修改是很简单的，要注意的是，如果修改了某一个位置的值，那么它的父亲节点的值也可能会发生改变，所以递归的时候要特别的注意。

5.区间查询：

区间查询可以说是基础线段树中最好理解的了~也是由递归写成，所以理解起来就会容易一些。

int Find(int root,int left,int right)//在区间[left,right]中查询最大值 
{
	//我们有的信息是当前结点所管辖的区域即[tree[root].left,tree[root].right]
	//要查询的区间和当前区间的关系无非两种。
	//一种是要查询的区间全部在当前区间的左边 
	//另一种是要查询的区间全部在当前区间的右边
	//最为普遍的就是一部分在左半区间，另一部分在右半区间
	//而上述三种情况到底是哪一种还是取决一个重要的参数，即当前结点管辖区域的中间结点，也即tree[root].mid 
	if(tree[root].left == left && tree[root].right == right)
		return tree[root].max;
	if(right <= tree[root].mid)//全部在左子树 
		return Find(root*2,left,right);
	else if(tree[root].mid < left)//全部在右子树 
		return Find(root * 2 + 1,left,right);
	else{//普遍情况，两边都有交集 
		int max1 = Find(root * 2,left,tree[root].mid);
		int max2 = Find(root * 2 + 1 , tree[root].mid + 1,right);
		return Max(max1,max2);
	}
	
};

—————————————————————————————————————————————————————————————————————————————

以上三个函数就是单点修改+区间查询的重要部分，推荐杭电的1754题练练手。

这里附AC代码供参考：

#include 
#include 
#define maxn 200005

typedef struct{
	int max;
	int left,right;//[left,right] 
}Tree;

int N,M;
int num[maxn];
Tree leaf[maxn * 5];//leaf[i]表示第几个i个叶节点,注意这个地方如果范围是maxn会数组越界 

int Max(int x,int y)
{
	return (x > y) ? x : y;
}
//更新index结点的值 
void Update(int root,int index,int value)
{
	if(leaf[root].left == index && leaf[root].right == index){
		//return leaf[root].max;
		leaf[root].max = value;//将成糹ndex == ǜ奈獀alue 
		return ;
	}
	int mid = (leaf[root].right + leaf[root].left) >> 1;
	if(index <= mid)
		Update(root*2,index,value);
	else if(mid < index)
		Update(root*2+1,index,value);
	leaf[root].max = Max(leaf[root*2].max,leaf[root*2 + 1].max);
};
void Build(int index,int left,int right)
{
	
	leaf[index].left = left;
	leaf[index].right = right;
	
	if(left == right){
		leaf[index].max = num[left];
		return ;
	}
	else{
		int mid = (left + right) >> 1;
		Build(index * 2,left,mid);
		Build(index * 2 + 1,mid + 1,right);
		leaf[index].max = Max(leaf[index*2].max,leaf[index*2+1].max);
	}
};
int Find(int root,int left,int right)
{
	if(leaf[root].left == left && leaf[root].right == right)
		return leaf[root].max;
	int mid = (leaf[root].left + leaf[root].right) >> 1;
	if(right <= mid)
		return Find(root * 2,left,right);
	else if(mid < left)
		return Find(root*2+1,left,right); 
	else{
		int max1 = Find(root*2,left,mid);
		int max2 = Find(root*2+1,mid+1,right);
		return Max(max1,max2);
	}
}

int main()
{
	int a,b,value;
	char Q;
	
	while(scanf("%d",&N) != EOF){
		scanf("%d",&M);
		memset(leaf,0,sizeof(leaf));
		memset(num,0,sizeof(num));
		for(int i = 1 ; i <= N ; ++i)
			scanf("%d",&num[i]);
		Build(1,1,N);//建立线段树,初始化,第一个1表示初始结点 
		getchar();
		for(int i = 0 ; i < M ; ++i){
			scanf("%c %d %d",&Q,&a,&b);
			getchar();
			if(Q == 'Q')
				printf("%d\n",Find(1,a,b));
			else{
				num[a] = b;
				Update(1,a,b);
			}
		}
	}
	return 0;
}

注意：因为线段树的建立、修改、查询都是基于递归函数，那么有一点不能忽略的就是递归出口的问题，应该时刻牢记

转载于:https://www.cnblogs.com/sixdaycoder/p/4348359.html