【 仿真 】基于TOA的定位算法性能分析(不同信噪比下的比较)
Comparison of Nonlinear and Linear Approaches with CRLB for TOA - Based Positioning for Different SNRs
上篇博文:【 笔记 】定位算法性能分析 给出了各种定位算法性能分析的理论知识。
这篇博文对它进行仿真分析,主要是求CRLB,我们这篇博文延续以前博文的惯例,求解各种定位算法的RMSE,这样的话,我们求得的CRLB在画图的时候也加上一个平方根。
条件:
Consider a 2 - D geometry of L = 4 receivers with known coordinates at (0, 0), (0, 10), (10, 0), and (10, 10), while the unknown source position is ( x , y ) = (2, − 3). Note that the source is located outside the square bounded by the four receivers. The range error variance, ![]() , is assigned proportional to
, is assigned proportional to ![]() with
with ![]() . Compare the RMSE performance of the nonlinear and linear approaches with the sqrt of CRLB for SNR ∈ [ − 10, 60] dB.
. Compare the RMSE performance of the nonlinear and linear approaches with the sqrt of CRLB for SNR ∈ [ − 10, 60] dB.
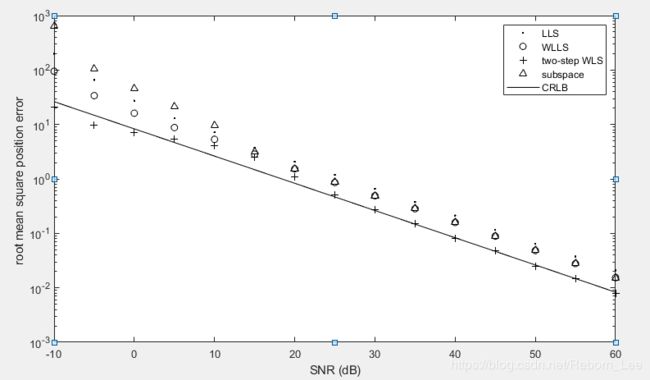
We compute the MSPE based on 1000 independent runs. The NLS and ML estimators are realized by the Newton –Raphson scheme, and their initial guesses are provided by the LLS and WLLS algorithms, respectively. The MSPEs of the nonlinear and linear approaches are shown in Figures 2.7 and 2.8 , respectively. In Figure 2.7 , we observe that the ML estimator is superior to the NLS method and its RMSE can attain the sqrt of CRLB for sufficiently high SNR conditions, namely, SNR ≥ 35 dB, which agrees with Equation 2.173 . In Figure 2.8 , it is seen that the two - step WLS estimator achieves optimal estimation performance at SNR ≥ 25 dB, while the LLS, WLLS, and subspace methods can only give suboptimal accuracy. Note that the MSPEs of the ML and two - step WLS estimators can be less than CRLB when SNR ≤ 0 dB because their estimates become biased for sufficiently large noise conditions.
下图(fig 2.5)是非线性算法的RMSE以及CRLB的对比:
下面(fig 2.6)是线性算法的RMSE及CRLB:
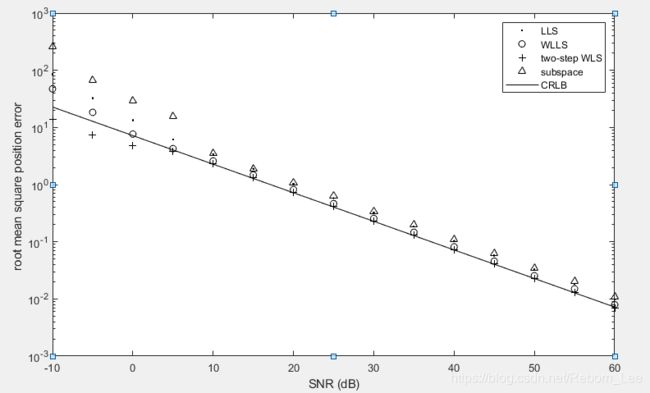
It is worthy to point out that the results of Figures 2.5 and 2.6 can also be produced from Example by modifying the source location. In doing so, we will again observe the optimality of the ML and two - step WLS estimators and the suboptimality of the NLS, LLS, WLLS, and subspace schemes. Note that the CRLB for ( x , y ) = (2, 3) is smaller than that of ( x , y ) = (2, − 3). This aligns with the conventional wisdom [30, 31] that better estimation performance can be achieved when the source location falls within the convex hull of the receivers.
当源位置变为: ( x , y ) = (2, 3)
上面的仿真对比图如下:
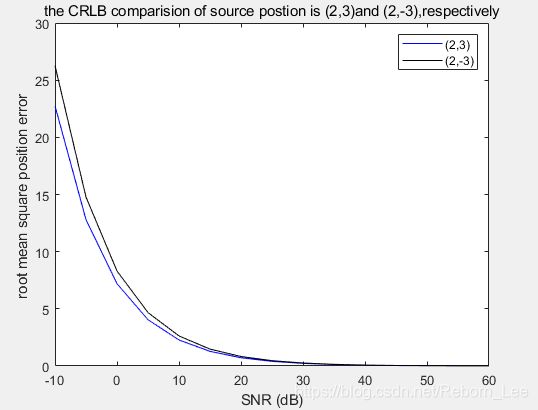
下面比较,源位置分别位于(2,3)与(2,-3)时候的CRLB的平方根曲线:
Note that the CRLB for ( x , y ) = (2, 3) is smaller than that of ( x , y ) = (2, − 3).
这说明,源位置对定位的精度也是有影响的,这符合我们的常识,四个测量站围着一个目标源位置,那么定位误差肯定要小一点。上图也说明了这个问题。
用官方的话说:
Note that the CRLB for ( x , y ) = (2, 3) is smaller than that of ( x , y ) = (2, − 3). This aligns with the conventional wisdom [30, 31] that better estimation performance can be achieved when the source location falls within the convex hull of the receivers.
这符合传统观点[30,31],当源位置落入接收器的凸包内时,可以实现更好的估计性能。