题目描述
对于任何正整数x,其约数的个数记作g(x)。例如g(1)=1、g(6)=4。
如果某个正整数x满足:g(x)>g(i) 0
现在给定一个数N,你能求出不超过N的最大的反质数么?
输入格式
一个数N(1<=N<=2,000,000,000)。
输出格式
不超过N的最大的反质数。
输入输出样例
输入 #1
1000
输出 #1
840
2019/8/21-更新(代码后面写不了了,只能写在前面...):
上午刚做的题,下午老师就讲了,搞得我好像白写了题解o(一︿一+)o,所以就顺便把老师的课件附上来吧!
(别忘了后面还有我自己写的...





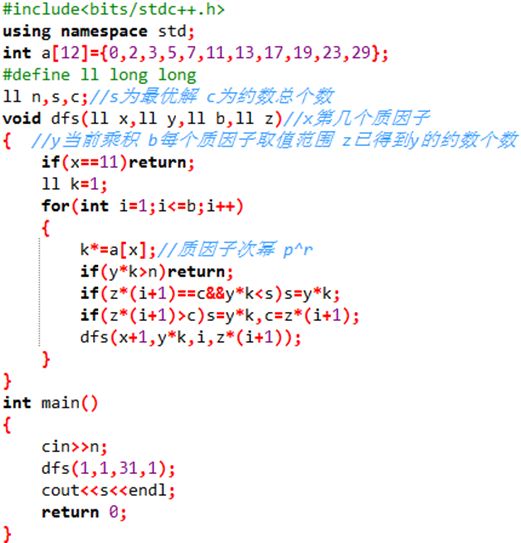
首先普及下关于“反素数”的两个性质:
-
性质一:一个反素数的质因子必然是从2开始连续的质数.
-
性质二:p=2^t1*3^t2*5^t3*7^t4.....必然t1>=t2>=t3>=....
然后,我再说下我个人的理解
-
因为题目给出了n的范围,所以我们可得出结论:n的质因子的种数不超过10,所以得到了一条递归边界;
-
因为“反素数”的性质二,所以在两个数约数相等的情况下,更小的那个数就是“反素数”(可以用反证法证明:如果存在a的约数个数与b相等,且a>b。若认为a为“反素数”,那么不满足小于a的数的约数个数都小于a的约数个数,矛盾;)。所以我们要求的答案显然就是不大于n的 约数个数最大的 最小的数(哇这句话真的要好好理解,性质二肥肠关键!;
-
那么应用到本题,在递归的过程中,如果遇到两个数约数个数相同,并且当前得到的数now小于之前得到的数ans,那就更新ans;如果当前求得的数now的约数个数num已经大于之前求到的最大的约数个数tot,那就更新tot,并且别忘了也要更新ans;
-
如果在递归过程中,当前求得值已经大于n,那么就没必要再继续递归下去,直接返回,这就是第二条递归边界;
-
在递归函数中设置一个循环,每进行一个循环,当前递归的质因子的个数就加一,并且此处还可以进行一点剪枝,在循环条件中加入“当前递归的质因子个数 不大于 比其小的质因子的 个数”这个条件;
我在这里给出两种代码,思想大概就是我上面所述,只不过写法略有不同,大家可以选择自己更喜欢的一种啦~
(顺便,看我码字不易,怎么说也给个“推荐”吧♪(^∀^●)ノ
1 #include
2 using namespace std;
3 const int N=1e6+5,inf=0x3f3f3f3f;
4 int a[11]={0,2,3,5,7,11,13,17,19,23,29};//打表大法好(质因子种数不超过10)
5 long long n,ans,tot;//tot为求到的最大的约数个数
6 void f(long long x,long long now,long long shu,long long num)
7 {
8 //x为当前递归的质因子,now为当前求得的数,num为now的约数个数
9 if(x==11)return ;//递归边界1
10 long long tmp=1,i;
11 for(i=1;i<=shu;i++)//当前递归的质因子的个数不超过shu(想不到其他变量名惹...无奈词汇量太小)
12 {
13 tmp*=a[x];//tmp暂时存储
14 if(now*tmp>n)return ;//递归边界2
15 if(num*(i+1)==tot&&now*tmp//如果约数个数相同,并且当前得到的数now小于之前得到的数ans,那就更新ans;
16 if(num*(i+1)>tot)//如果now的约数个数num大于之前求到的最大的约数个数tot,那就更新tot,并且更新ans;
17 {
18 tot=num*(i+1);
19 ans=now*tmp;
20 }
21 f(x+1,now*tmp,i,num*(i+1));//往下递归
22 }
23 }
24 int main()
25 {
26 cin>>n;
27 f(1,1,31,1);
28 printf("%lld",ans);
29 return 0;
30 }
我比较喜欢下面的代码↓↓↓
1 #include
2 using namespace std;
3 const int N=1e6+5,inf=1<<29;
4 int a[11]={0,2,3,5,7,11,13,17,19,23,29},used[11];//used[i]是指表中第i个质因子的个数
5 long long n,ans,tot;
6 void f(long long id,long long now,long long num)
7 {
8 //id指当前递归的是表中的第几个质数,now和num同上一种做法
9 if(num>tot)//同上一种做法
10 {
11 ans=now;
12 tot=num;
13 }
14 if(num==tot&&now//同上一种做法
15 used[id]=0;//注意每次递归要更新
16 while(now*a[id]<=n&&used[id]+1<=used[id-1])//循环条件中也包含了递归边界2(然鹅这里没有用递归边界1
17 {
18 now*=a[id];//now更新
19 used[id]++;//当前递归的质因子个数加一
20 f(id+1,now,num*(used[id]+1));//继续递归
21 }
22 }
23 int main()
24 {
25 cin>>n;
26 used[0]=inf;//注意!要保证在对第一个质数进行递归的时候,循环可以进行下去,详见used[id]+1<=used[id-1]
27 f(1,1,1);
28 printf("%lld",ans);
29 return 0;
30 }





