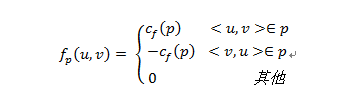网络流之最大流

一、残留网络及增广路

　　残留网络、增广路及割是构成最大流最小割定理的三个基本概念，该定理巧妙地运用网络中的最小割来描述最大流的值。

1.残留网络

　　对于网络G=(V,E,C)，设流f是G中的流。残留网络直观上讲是由还可以容纳更多的流的边组成。对于G中的每条边，可以定义残留容量为在不超过容量限制的条件下，可以通过的额外的网络流量

cf(u,v)=c(u,v)-f(u,v)

　　事实上，残留网络也是一个网络，容量由cf给出。设f是网络G=(V,E,C)的一个流，f1是残留网络Gf的一个流，则f+f1依然是网络G的一个流。这个引理给出了残留网络与原网络的关系，也为提出增广路1提供了前提。

2.增广路

　　定义：增广路p为残留网络Gf上的源s到汇t的一条简单路径。该路径的残留容量为可以沿该路径增加的最多额外流量：cf(p)=min{cf(u,v) | ∈p}。这个值是严格大于0的。

　　从上面的描述可以推导出增广路的可增广性质，定义流fp为

给定网络G中的一个流f，则f+fp依然是网络G的一个流。

 

二、最小割最大流定理

1.割

　　网络G=（V,E,C)中割[S,T]将点集V划分为S、T(S=V-T)两个部分，使得s∈S且t∈T。符号[S,T]代表边集合{| ∈E, u∈S, v∈T}。穿过割[S,T]的净流定义为f(S,T)，割[S,T]的容量定义为c(S,T)。一个网络的最小割也就是该网络中的容量最小的割。

2.最小割最大流定理

　　可以完整描述最小割最大流定理如下：

　　如果f是具有源s和汇t的网络G={V,E,C}中的一个流，则下列条件是等价的：

　　(1)f是G的一个最大流；

　　(2)残留网络Gf不包含增广路径；

　　(3)对G的某个割[S,T],有|f|=c(S,T)。

 

三、最大流算法

1.Ford-Fulkson方法的基本思想

　　Ford-Fulkson（简称FF）方法是由Ford和Fulkson两位数学家发明的。充分利用最小割最大流定理，并创造性地发明了回退边，使得增广成为一种动态修改的过程，并且保证了最终结果的正确性。

　　FF方法的具体步骤：

　　（1）初始化网络中所有边的容量，c继承该边的容量，c初始化为0，其中边即为回退边。初始化最大流为0。

　　（2）在残留网络中找一条从源S到汇T的增广路p。如能找到，则转步骤（3）；如不能找到，则转步骤（5）。

　　（3）在增光路p中找到所谓的“瓶颈”边，即路径中容量最小的边，记录下这个值X，并且累加到最大流中，转步骤（4）。

　　（4）将增广路中所有c减去X，所有c加上X，构成新的残留网络。转步骤（2）。

　　（5）得到网络的最大流，退出。

　　《算法导论》中严格定义FF方法为一种方法而非算法，也许正是因为FF方法中的第（2）步并未给出具体的寻找增广路方法。寻找增广路方法的不确定导致时间复杂度的不确定。后面将发现，能否高效地寻找增广路将是各种算法优劣的主要判断。

 

三、Edmond-Karp算法

　　Edmond-Karp算法作为FF类算法中最简单的一个算法，算法流程与FF方法流程完全相同，但是在处理寻找增广路上使用到了朴素的BFS。由于BFS的最短路性质，所以又称EK算法为最短增广路算法。

　　1.算法实现

 1 #include
 2 #include
 3 #include
 4 #include<set>
 5 #include
 6 #include
 7 #include<string>
 8 
 9 using namespace std;
10 const int inf = 0x3f3f3f3f;
11 const int N = 222, M = N * N << 1;
12 int first[N], Next[M];
13 int tot, p;
14 struct EG {
15     int u, v, cap;
16     EG(){}
17     EG(int u, int v, int cap): u(u), v(v), cap(cap){}
18 } eg[M];
19 void init()
20 {
21     tot = p = -1;
22     memset(first, -1, sizeof(first));
23 }
24 void add_edge(int u, int v, int cap)
25 {
26     eg[++tot] = EG(u, v, cap);
27     Next[tot] = first[u], first[u] = tot;
28     eg[++tot] = EG(v, u, 0);
29     Next[tot] = first[v], first[v] = tot;
30 }
31 
32 // Edmond-Karp
33 int pre[N]; //记录前驱边的编号
34 bool EK_BFS(int s, int t)
35 {
36     queue<int> q;
37     bool vis[N];
38     memset(vis, 0, sizeof(vis));
39     memset(pre, -1, sizeof(pre));
40     q.push(s);
41     vis[s] = 1;
42     while(!q.empty())
43     {
44         int u = q.front(); q.pop();
45         if(u == t) return true;
46         for(int i=first[u]; i!=-1; i=Next[i])
47         {
48             EG &e = eg[i];
49             if(e.cap > 0 && !vis[e.v])  //当边的容量为非零，且增广点未标记
50             {
51                 vis[e.v] = 1;
52                 pre[e.v] = i;   //记录前驱
53                 q.push(e.v);
54             }
55         }
56     }
57     return false;
58 }
59 
60 int EK_Max_Flow(int s, int t)
61 {
62     int Max_Flow = 0;
63     while(EK_BFS(s, t))
64     {
65         int mn = inf;
66         int now = t;
67         while(pre[now] != -1) {
68             mn = min(mn, eg[pre[now]].cap);
69             now = eg[pre[now]].u;
70         }
71         Max_Flow += mn;
72         now = t;
73         while(pre[now] != -1)
74         {
75             eg[pre[now]].cap -= mn;
76             eg[pre[now]^1].cap += mn;
77             now = eg[pre[now]].u;
78         }
79     }
80     return Max_Flow;
81 }
82 
83 int main()
84 {
85     /* 模板测试：poj 1273
86        输入m, n及m条边，求1~n最大流 */
87     int n, m;
88     while(scanf("%d %d", &m, &n) == 2)
89     {
90         init();
91         int u, v, cap;
92         for(int i=1; i<=m; i++) {
93             scanf("%d %d %d", &u, &v, &cap);
94             add_edge(u, v, cap);
95         }
96         printf("%d\n", EK_Max_Flow(1, n));
97     }
98     return 0;
99 }

View Code

　　可以证明EK算法中使用BFS增广时增广次数不超过V*M次，而每次BFS时间复杂度都是O（M），所以EK算法的时间复杂度为O（V*M²）。

　　需要注意的是，每次增广结束后，都需要对回退边进行处理，否则EK算法将失去准确性。

 

四、SAP算法及其优化

　　如果能让每次寻找增广路时的时间复杂度降下来，那么就能提高算法效率，使用距离标号的最短增广路SAP算法就是这样。距离标号的思想来源于push_relable类算法。

　　（1）距离标号及其维护

　　距离标号为某个点到汇点的最少的边的数量。设点i的标号为D[i]，那么如果将满足D[i]=D[j]+1的边称作允许弧，且增光时只走允许弧，那么就可以达到“怎么走都是最短路”的效果。每个点的初始标号可以在一开始用一次从汇点沿所有反向边的BFS求出，实践中可以初始设全部点的距离标号为0。维护距离标号的方法是：当找增广路过程中发现某点出发没有允许弧时，将这个点的距离标号设为由它出发的所有边的终点的距离标号的最小值加1。这种维护距离标号的方法显然是正确的。由于距离标号的存在，“怎么走都是最短路”，所以就可以采用DFS找增广路，用一个栈保存当前路径的弧即可。当某个点的距离标号被改变时，栈中指向它的那条弧肯定已经不是允许弧了，所以就让它出栈，并继续用栈顶的弧的端点增广。

　　（2）SAP算法的几个优化

　　为了使每次找增广路的时间变成均摊O（n²），有一个重要的优化就是对于每个点保存“当前弧”：初始时当前弧是邻接表的第一条弧；在邻接表中查找时从当前弧开始查找，找到一条允许弧，就把这条弧设为当前弧；改变距离标号时，把当前弧重新设为邻接表的第一条弧，还有一种在常数上有所优化的写法是改变距离标号时把当前弧设为那条提供了最小标号的弧。当前弧的写法之所以正确就在于任何时候都能保证在邻接表中当前弧的前面肯定不存在允许弧。

　　还有一个常数优化是在每次找到路径并增广完毕后不要将路径中所有的顶点退栈，而是只将瓶颈边以及之后的边退栈，这是借鉴了Dinic算法的思想。而该优化也使得一次增广能够找到更多的流。

　　通过上面的介绍，了解到两种优化：邻接表的使用使得当前弧优化成为可能；借鉴自Dinic的多路增广思想使得每次增广的效率得到提高。下面还将给出一个更为高效的优化。

　　定理：当网络中的距离标号出现断层时，残余网络中无法得到新流。

　　SAP算法的标号思想继承自push_relable算法，自然GAP优化也可以完全继承过来。这个优化只需要一个数组加一句话，但是却大大降低了算法时间复杂度的常数，效率很高。

　　（3）算法实现

  1 #include
  2 #include
  3 #include
  4 #include<set>
  5 #include
  6 #include
  7 #include<string>
  8 
  9 using namespace std;
 10 const int inf = 0x3f3f3f3f;
 11 const int N = 222, M = N * N << 1;
 12 int first[N], Next[M];
 13 int tot, p;
 14 struct EG {
 15     int u, v, cap;
 16     EG(){}
 17     EG(int u, int v, int cap): u(u), v(v), cap(cap){}
 18 } eg[M];
 19 void init()
 20 {
 21     tot = p = -1;
 22     memset(first, -1, sizeof(first));
 23 }
 24 void add_edge(int u, int v, int cap)
 25 {
 26     eg[++tot] = EG(u, v, cap);
 27     Next[tot] = first[u], first[u] = tot;
 28     eg[++tot] = EG(v, u, 0);
 29     Next[tot] = first[v], first[v] = tot;
 30 }
 31 
 32 //SAP
 33 int SAP_Max_Flow(int s, int t)
 34 {
 35     int numh[N], h[N], curr[N], pre[N];
 36     ///numh:用于GAP优化的统计高度数量数组；h：距离标号数组；curr：当前弧数组；pre：前驱数组
 37     int Max_Flow = 0, curr_flow;
 38     int neck;  //瓶颈边
 39     memset(h, 0, sizeof(h));
 40     memset(numh, 0, sizeof(numh));
 41     memset(pre, -1, sizeof(pre));
 42     for(int i=1; i<=N; i++) curr[i] = first[i];
 43     numh[0] = N;
 44     int now = s;
 45     while(h[s] < N)
 46     {
 47         if(now == t)
 48         {
 49             curr_flow = inf;
 50             //找瓶颈
 51             for(int i=s; i!=t; i=eg[curr[i]].v)
 52             {
 53                 if(curr_flow > eg[curr[i]].cap) {
 54                     neck = i;
 55                     curr_flow = eg[curr[i]].cap;
 56                 }
 57             }
 58             //修改边容量
 59             for(int i=s; i!=t; i=eg[curr[i]].v)
 60             {
 61                 int tmp = curr[i];
 62                 eg[tmp].cap -= curr_flow;
 63                 eg[tmp^1].cap += curr_flow;
 64             }
 65             Max_Flow += curr_flow;
 66             now = neck;   //下次增广从瓶颈开始
 67         }
 68         int i;
 69         for(i=curr[now]; i!=-1; i=Next[i])
 70             if(eg[i].cap>0 && h[now] == h[eg[i].v]+1)
 71             break;  //寻找可行弧
 72         if(i != -1)
 73         {
 74             curr[now] = i;
 75             pre[eg[i].v] = now;
 76             now = eg[i].v;
 77         }
 78         else
 79         {
 80             if(0 == --numh[h[now]]) break;   //GAP优化
 81             curr[now] = first[now];
 82             int i, tmp;
 83             for(i=first[now], tmp=N; i!=-1; i=Next[i])
 84                 if(eg[i].cap > 0)
 85                 tmp = min(tmp, h[eg[i].v]);
 86             h[now] = tmp + 1;
 87             ++numh[h[now]];
 88             if(now != s) now = pre[now];
 89         }
 90     }
 91     return Max_Flow;
 92 }
 93 int main()
 94 {
 95     /* 模板测试：poj 1273
 96        输入m, n及m条边，求1~n最大流 */
 97     int n, m;
 98     while(scanf("%d %d", &m, &n) == 2)
 99     {
100         init();
101         int u, v, cap;
102         for(int i=1; i<=m; i++) {
103             scanf("%d %d %d", &u, &v, &cap);
104             add_edge(u, v, cap);
105         }
106         printf("%d\n", SAP_Max_Flow(1, n));
107     }
108     return 0;
109 }

View Code

 

 

五、Dinic算法

　　该算法由Dinic于1970年提出，Dinic算法关注的还是怎样减少增广次数。SAP算法通过构造距离标号，使得每次增广的效率提高，而Dinic则构造了分层网络使得一次增广可以找到更多的流。

　　1.分层网络与多路增广

　　Dinic算法在找增广路之前会有一步类似SAP的为顶点定标的过程，通常为BFS。在BFS中，通过一个顶点向其邻接点增广的依据是两者之间是否有正容量边存在，并且将顶点遍历的时间戳设定为顶点标号A[i]。很显然如果一次BFS能够成功地从源点增广到汇点，整个网络根据顶点标号将会变成一个层次网络，每个顶点都将有自己的层数。

　　在一个分层网络中，只有A[i]=A[j]或者A[i]=a[j]-1时，之间有边存在。当且仅当A[i]=A[j]-1时，两点之间的边称作有用边，在接下来的寻找增广路过程中只会走这样的有用边。因此，在BFS时，只要遍历到汇点即可停止，因为按照该规定，与汇点同层或更下一层的节点不可能走到汇点。

　　与SAP类似，分层网络的运用使得在其中增广也会是“怎么走都是最短路”。

　　当为残留网络分完层后，就可以使用多路增广路了，一般的手段是DFS。从源点开始，用DFS从前一层向后一层反复寻找增广路。DFS过程中，如果碰到了汇点，则说明找到了一条增广路径。此时要增加总流量的值，削减路径上各边的容量，并添加反向边，即进行增广。DFS找到一条增广路径后，并不立即结束，而是回溯后继续DFS，寻找下一个增广路径。

　　如果回溯到源点而且无法继续往下走了，DFS结束。因此，一次DFS过程中，可以找到多条增广路。

　　DFS结束后，对残余网络再次进行分层，然后再进行DFS，当残余网络的分层操作无法算出汇点的层次（即BFS到达不了汇点）时，算法结束，最大流求出。

 

2.算法实现与分析

  1 #include
  2 #include
  3 #include
  4 #include<set>
  5 #include
  6 #include
  7 #include<string>
  8 
  9 using namespace std;
 10 const int inf = 0x3f3f3f3f;
 11 const int N = 222, M = N * N << 1;
 12 int first[N], Next[M];
 13 int tot, p;
 14 struct EG {
 15     int u, v, cap;
 16     EG(){}
 17     EG(int u, int v, int cap): u(u), v(v), cap(cap){}
 18 } eg[M];
 19 void init()
 20 {
 21     tot = p = -1;
 22     memset(first, -1, sizeof(first));
 23 }
 24 void add_edge(int u, int v, int cap)
 25 {
 26     eg[++tot] = EG(u, v, cap);
 27     Next[tot] = first[u], first[u] = tot;
 28     eg[++tot] = EG(v, u, 0);
 29     Next[tot] = first[v], first[v] = tot;
 30 }
 31 
 32 int level[N];
 33 int curr[N];
 34 bool BFS(int s, int t)
 35 {
 36     queue<int>q;
 37     memset(level, 0x3f, sizeof(level));
 38     level[s] = 0;
 39     q.push(s);
 40     while(!q.empty())
 41     {
 42         int u = q.front(); q.pop();
 43         for(int i=first[u]; i!=-1; i=Next[i])
 44         {
 45             EG &e = eg[i];
 46             if(e.cap > 0 && level[e.v] == inf)
 47             {
 48                 level[e.v] = level[u] + 1;
 49                 q.push(e.v);
 50             }
 51         }
 52     }
 53     return level[t] != inf;
 54 }
 55 int dinic(int u, int t, int flow)
 56 {
 57     if(u == t) return flow;
 58     for(int i=curr[u]; i!=-1; i=Next[i])
 59     {
 60         curr[u] = i;
 61         EG &e = eg[i];
 62         if(e.cap > 0 && level[e.v] == level[u] + 1)
 63         {
 64             int tp = dinic(e.v, t, min(flow, e.cap));
 65             if(tp)
 66             {
 67                 e.cap -= tp;
 68                 eg[i^1].cap += tp;
 69                 return tp;
 70             }
 71         }
 72     }
 73     return 0;
 74 }
 75 int DINIC(int s, int t)
 76 {
 77     int ans = 0;
 78     while(BFS(s,t))
 79     {
 80         int  tp;
 81         for(int i=0; i<=t; i++) curr[i] = first[i];
 82         while(tp = dinic(s,t,inf))
 83             ans += tp;
 84     }
 85     return ans;
 86 }
 87 
 88 int main()
 89 {
 90     /* 模板测试：poj 1273
 91        输入m, n及m条边，求1~n最大流 */
 92     int n, m;
 93     while(scanf("%d %d", &m, &n) == 2)
 94     {
 95         init();
 96         int u, v, cap;
 97         for(int i=1; i<=m; i++) {
 98             scanf("%d %d %d", &u, &v, &cap);
 99             add_edge(u, v, cap);
100         }
101         printf("%d\n", DINIC(1, n));
102     }
103     return 0;
104 }

View Code

 　　Dinic算法的退出条件是BFS无法遍历到汇点，换句话说，就是整个网络的层数已经超过了点数n，最坏情况下，每次增广都会使得最大层数加1，则算法最多执行增广n次，且由于每次增广的时间复杂度都是O(n*m)，所以最终的时间复杂度为O(n²*m)。算法在具体实现上可以使用实际效果稍好的邻接表；在实现DFS过程中，也可以使用更加简洁的递归，但是会牺牲不少的时间效率。算法的空间复杂度为O(M)

 

小结练习

 

转载于:https://www.cnblogs.com/WCB-ACM/p/5233367.html