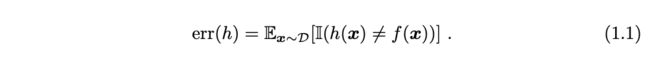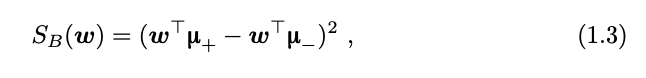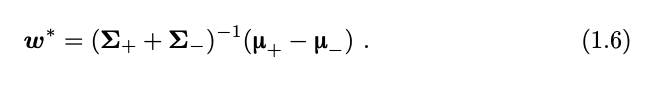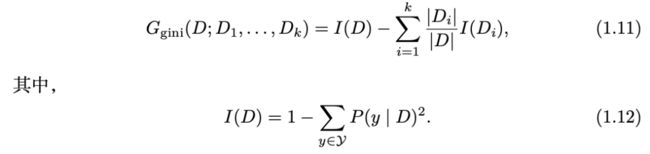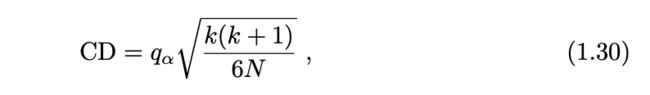周志华教授力作，豆瓣10分好评，集成学习如何破解AI实践难题 | 赠书

本文内容节选自《集成学习：基础与算法》一书。由南京大学人工智能学院院长周志华教授编著，中文版由其学生李楠博士翻译。

回顾机器学习最近30 年的发展历程，各种学习方法推陈出新、不断演进。但是，在此历程中，通过构建并结合多个学习器来完成学习任务的集成学习方法，始终是提升学习效果的重要手段，成为机器学习领域的“常青树”，受到学术界和产业界的广泛关注。

集成学习技术已在人工智能实践中被广泛使用，例如，对搜索、推荐、广告的核心任务——点击率预估而言，GBDT （Gradient Boosting Decision Trees）因其稳定、优异的效果一直是事实上的工业标准；在语音识别领域，基于集成深度学习的声学模型极大提升了识别效果；在异常检测上，iForest 因其极高的检测效率在实践中备受关注。

本书化繁为简，用通俗易懂的表述方式重点讲解集成学习的主流代表性技术 Boosting ，并详释了重要算法的实现。集成学习方法在实践中获得了巨大成功，本书也向读者阐述了集成学习在如计算机视觉、医疗、信息安全和数据挖掘竞赛等领域中的应用实践 。

想要了解关于集成学习的更多干货知识，关注AI科技大本营并评论分享你对本文的学习心得或集成学习的见解，我们将从中选出10条优质评论，各送出《集成学习：基础与算法》一本。活动截止时间为7月25日晚8点。

基本概念

机器学习、模式识别和数据挖掘的一项主要任务就是基于“数据集”(data set)构建“好”的“模型”(model)。

一个“数据集”通常由一组特征向量构成，其中每个特征向量使用一组“特征”(feature)来描述一个对象。例如，在图 1.1 中所示的 3-高斯人造数据集中， 每个对象就是一个被特征 x 坐标、y 坐标和形状所表述的数据点，相应的特征 向量可写成(.5, .8, cross)或(.5, .8, circle)。数据集中特征的数量被称为“维 度”(dimension);例如，上述数据集的维度为 3。通常，“特征”也会被称为

“属性”，一个“特征向量”也会被称为一个“示例”(instance)，一个“数据集” 也会被称为一个“样本集”(sample)。

一个“模型”通常指一个预测模型或者从数据集中构建的数据结构的模 型;例如，决策树、神经网络、支持向量机等。从数据中构建模型的过程称为“学习”(learning)或“训练”(training)，这一过程由“学习算法”(learning algorithms)来完成。学习获得的模型被称为“假设”(hypothesis)，在本书中 会被称为“学习器”(learner)。

现实中有不同类型的学习问题，其中最常见的是“监督学习”(supervised learning)和“无监督学习”(unsupervised learning)。监督学习的目标是预测 未见样本的目标特征的值，此时学习获得的模型被称为“预测器”(predictor)。例如，在 3-高斯数据集上，如果要预测数据点的形状，“cross”和“circle”被 称为“标记”(labels)，预测器应该能够预测未知标记样本的标记，如预测数据点(.2, .3)的形状。

如果标记是类别(categorical)变量，如这里的“形 状”，此学习任务被称为“分类”(classification)，相应的学习器被称为“分类 器”(classifier);如果标记是数值(numerical)变量，如这里的“x 坐标”，此学 习任务被称为“回归”(regression)，相应的学习器被称为“回归模型”(fitted regression model)。在两种情况下，学习过程都是在具有标记信息的数据集上 完成的;此时，一个具有标记的示例称为一个“样本”(example)。在“二分 类”(binary classification)中，我们通常使用“正”和“负”表示两个类别标记。

无监督学习不依赖于标记信息，它的目标是发现数据的一些内在分 布信息。一个典型的任务就是“聚类”(clustering)，即:发现数据点内在的 “簇”(cluster)结构。在本书中，我们主要关注监督学习，尤其是分类。在 1.2 节中，我们将简要介绍一些常用的学习算法。

通常来讲，一个模型“好”还是“不好”取决于它是否能满足用户的需求。由于不同的用户对学习结果有不同的期望，在相应任务没有完成前，很难知道 什么是“正确的期望”。一个常用的策略就是评测并估计模型的效果，并让用户 决定一个模型是否可用，或者让用户从一组候选模型中选择最好的模型。

由于学习的根本目标是“泛化”(generalization)，即:能够把从训练样本 学习获得的知识推广到未见样本，因此一个好的学习器应该具有好的泛化能力， 即:具有较小的“泛化误差”(generalization error)。但是，直接估计泛化误差 需要知道未见样本的“真实”(ground-truth)标记，因此实际操作中是不可行 的。

此时，代表做法是让学习器对已知真实标记信息的“测试数据”(test data) 进行预测，并将计算获得的“测试误差”(test error)作为泛化误差的估计。将 学习获得的模型应用到未见数据上的过程，称为“测试”(testing)。在测试前， 通常需要对学习获得的模型进行合适的配置，如:调整参数，此过程需要使用具有真实标记的数据来评估学习效果，被称为“验证”(validation)，使用的相应数据被称为“验证数据”(validation data)。一般来讲，测试数据不能包含 训练数据和验证数据，否则估计的效果会过于乐观。1.3 节将介绍效果评估。

学习过程可以形式化地描述为如下过程。假设 X 为样本空间，D 为 X 上 的分布，f 为潜在目标函数。给定训练集 D = {(x1, y1), (x2, y2), . . . , (xm, ym)}， 其中 xi 是来自分布 D 的独立同分布取样且 yi = f(xi)。以分类为例，学习的 目标是构建学习器 h 以最小化泛化误差

常用学习算法

1.2.1 线性判别分析

线性分类器由权重向量 w 和偏差项 b 构成。给定样例 x，其按如下规则预测获得类别标记 y，即

分类过程分为如下两步:首先，使用权重向量 w 将样本空间投影到直线上;然 后，寻找直线上的一个点把正样本和负样本分开。

为了寻找最优的线性分类器(即:w 和 b)，一个经典的学习算法是线性判别分析(Fisher’s linear discriminant analysis，LDA)。简要来讲，LDA 的基本想法是使不同类的样本尽量远离，同时使同类样本尽可能靠近。这一目标可通 过扩大不同类别样本的类中心距离，同时缩小每个类的类内方差来实现。

在一个二类数据集上，分别记所有正样本的均值和协方差矩阵为 μ+ 和Σ+，所有负样本的均值和协方差矩阵为。投影后的类中心的距离为

同时，类内方差可写为

基于此，线性判别分析最大化以下目标以获取最优的权重向量，即

此问题的最优解可写为

获取权重向量 w 后，不难获得偏差项 b。例如，如果两类样本都来自具有相同 方差的正态分布，偏差项 b 的最优解就是两个类中心的均值，即

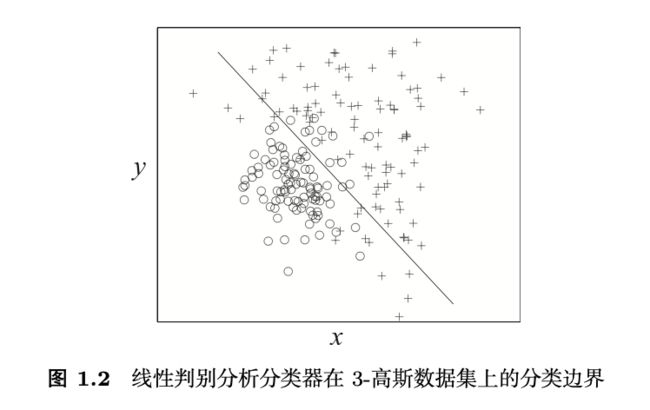
图 1.2 给出了线性判别分析分类器在 3-高斯数据集上的分类边界。

1.2.2 决策树

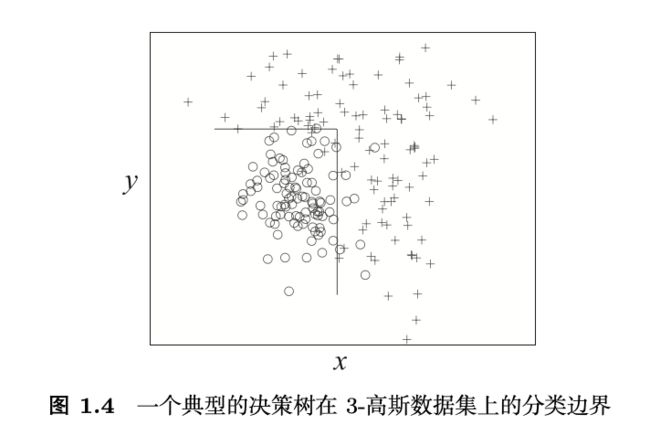
一棵决策树(decision tree)由一系列按“分而治之”(divide-and-conquer) 方式组织的树状决策测试构成。每个非叶节点上有一个特征测试(也称“分 割”);基于特征测试中不同的特征取值，节点中的数据被分成不同的子集。每 个叶节点具有一个类别标记，每个落到此叶节点的示例会被设置为此类别标记。预测时，从根节点开始，样本经过一系列特征测试到达叶节点，进而获得预测 结果。以图 1.3 为例，分类过程以检测 y 坐标的值是否大于 0.73 开始;如果是， 此示例被分类为“cross”，否则检测决策树测试 x 坐标是否大于 0.64;如果是， 示例将被分类为“cross”，否则为“circle”。

决策树学习算法通常是递归过程。在每一步执行中，给定数据集并选定分 割，数据集被此分割分成几个子集;每个子集作为下一步执行中的给定数据集。不难发现，决策树学习算法的核心是如何选择分割。

ID3 算法 [Quinlan，1986] 选择信息增益(information gain)作为分割准则。给定训练集 D，此数据集的熵(entropy)定义为

如果数据集 D 被分成子集 D1,...,Dk，相应的熵会减少，所减少的熵被称为“信息增益”，即

基于此，能够产生最大信息增益的“特征-值”组合会被选作分割。

信息增益准则的一个问题是它会偏爱那些具有很多可能取值的特征，而忽 略其和分类的相关性。例如，考虑我们在处理一个二分类任务，且每个样例有一 个唯一的“id”，此时若选择“id”作为一个特征并且将其作为分割的特征，将 会获得很大的信息增益，因为它能够正确分类所有的训练样本;但是，这样的 分类结果却不能泛化，不能用于对未见样例进行预测。

信息增益的这一不足在著名的 C4.5 算法 [Quinlan，1993] 中被解决。具体 而言，C4.5 算法使用“信息增益率”(gain ratio)作为选择分割的标准，即

不难发现，在信息增益的基础上，信息增益率使用特征的取值数做归一化。这 样，在所有具有较好信息增益的特征中，具有最高信息增益率的特征被选择作 为分割。

CART 算法 [Breiman et al.，1984] 也是一种著名的决策树算法，它使用“基尼系数”(Gini index)作为分割准则，即

对于决策树来讲，经常可以观察到一种现象:相对于在训练集上表现不那么 好的决策树，一棵在训练集上表现完美的决策树可能具有更差的泛化能力。这种 现象被称为“过拟合”(overfitting)，这是由于学习器误把训练数据集上的一些 特质当成潜在的真实数据分布造成的。例如，学习器可能拟合了训练数据集上 的噪音。

为了降低过拟合的风险，常用策略是使用“剪枝”(pruning)去除由于 训练数据集上的噪声或特质而产生出来的分枝。通常，“预剪枝”(pre-pruning) 在树生长时执行剪枝操作，而“后剪枝”(post-pruning)在树生长完成后再检 查并决定去除哪些分枝。如果有验证数据集，可以根据验证误差执行剪枝，即: 对预剪枝，如果验证误差上升，分枝就不能生长;对后剪枝，如果去除一个分 枝会造成验证误差降低，则执行剪枝。

早期的决策树算法，如 ID3，仅能处理离散特征;后期的算法，如 C4.5 和CART，能够处理数值特征。处理数值特征最简单的方式就是，评估选择数值特 征的每个取值作为分割点，并据此将数据集分成两个子集，其中一个包含比分 割点大的样本，另一个包含其余样本。

当决策树的高度被限制为 1 时，它预测时仅执行一个测试，这种决策树被 称为“决策树桩”(decision stump)。通常来讲，决策树是非线性分类器，而决 策树桩是线性分类器。

图 1.4 给出了一个典型的决策树在 3-高斯数据集上的分类边界。

1.2.3 神经网络

神经网络(neural network)，也称人工神经网络，源自对生物神经网络的 仿真和模拟。一个神经网络的功能由神经元(neuron)模型、网络结构和学习 算法共同决定。

神经元，也称神经单元(unit)，是神经网络中的基本计算组件。最常用的神经元模型是 McCulloch-Pitts 模型(简称 M-P 模型)。如图 1.5(a) 所示，在M-P 模型中，输入信号首先和连接权重相乘，然后相加累计后和一个称为激发阈值的偏置项比较。若累计信号值大于激发阈值，将激发神经元并由激活函数(activation function)产生输出信号。

神经元由带权重的链接连接构成网络，并能形成多种可能的网络结构。其中最著名的就是如图 1.5(b) 所示的多层前馈网络(multi-layer feed-forwardnetwork)。在该网络中，神经元按层连接，没有层内和跨层连接。输入层 (input layer)接收输入特征向量，每个神经元对应特征向量的一维，且其激活 函数被设置为 f(x) = x。输出层(output layer)输出标记，其中每个神经元通 常对应一个可能的标记或标记向量的一维。输入层和输出层之间的层被称为隐 层(hidden layer)。隐层神经元和输出层神经元是功能性单元，常用的激活函数是 sigmoid 函数，即

虽然可以使用多个隐层，但是大家还是经常使用具有一个或两个隐层的神 经网络。这是由于:第一，理论上具有一个隐层的前馈网络已经有能力逼近任 意连续函数;第二，训练具有多个隐层的网络需要复杂的学习算法防止其陷入 发散状态(即:神经网络难以收敛到稳定状态)。

神经网络训练的目的是决定其连接权重和神经元的激发阈值，这些值决定 了神经网络所代表的函数。不难发现，如果激活函数可微，整个多层前馈神经 网络就是关于这些参数的可微函数，此时最为常用的训练思路就是梯度下降(gradient descent)方法。

误差逆传播(BP)算法 [Werbos，1974;Rumelhart et al.，1986] 是最为成功的神经网络训练算法。在该算法中，输入经过输入层、隐层前馈计算到达输 出层，在输出层中对网络输出和样本标记进行比较并计算误差;然后，这些误 差再经过隐层反向传播回输入层，在传播的过程中算法会调整连接权重和激发 阈值以降低误差。整个过程按梯度方向调节各个参数的值，并执行多轮，直到 训练误差减小到预定目标范围。

1.2.4 朴素贝叶斯

为了对测试样例 x 进行分类，学习算法可以构建概率模型来估计后验概 率 P(y | x)，并选取具有最大后验概率值的 y 作为输出;这就是最大后验(maximum a posteriori，MAP)准则。基于贝叶斯定理，

在上式中，P(y) 可以通过计算训练数据中每个类的比例获得;由于是在同一个 x 上比较不同 y，P(x) 可被忽略。因此，仅需考虑 P(x | y)，如果能够获 得 P(x | y) 的精确估计，就能获得理论上的最优分类器，即具有理论上最小 错误率——贝叶斯错误率(Bayes error rate)——的贝叶斯最优分类器(Bayes optimal classifier)。但是，由于 P (x | y) 是联合概率分布，需要估计指数多的特征组合数量，直接估计将十分困难。为此，需要引入一些假设，以使估计变得可行。

朴素贝叶斯分类器(naïve Bayes classifier)假设给定类别标记，n 个特征之间是独立的。因此，这意味着，仅需在每个类内部计算每个特征取值的比例，从而避免了对联合概 率的估计。

在训练阶段，朴素贝叶斯分类器对所有类别 y ∈ Y 估计 P (y)，并对所有特 征 xi 估计 P (xi | y)。在测试阶段，在所有类别标记中，朴素贝叶斯分类器通过最大化

选择测试样例 x 的类别标记。

1.2.5 k-近邻

k-近邻(k-NN)算法的基本假设是输入空间中相似的样本在输出空间中也 应该相似。它没有显式的训练过程，仅需存储所有的训练样本，是一个懒惰学习 (lazy learning)方法。测试时，对测试样例 x，k-近邻算法在训练样本中寻找与 测试样本最近的 k 个近邻。对分类任务，测试样例被分类为 k 个近邻样本中的投票最高的类别;对回归任务，测试样例被预测为 k 个近邻样本的标记的均值。图 1.6(a) 给出了一个 3-近邻算法分类的示意图。

图 1.6(b) 给出了在 3-高斯数据集上 1-近邻分类器——也称最近邻分类器——的分类边界。

1.2.6 支持向量机和核方法

支持向量机(SVMs)[Cristianini & Shawe-Taylor，2000] 是用来解决二分类问题的大间隔分类器(large margin classifier)，它尝试寻找具有最大间隔(margin)的超平面来区分不同类别的样本。其中，间隔定义为不同类别的样本到分类超平面的距离。

考虑线性分类器 y = sign(w⊤x + b) (缩写为 (w, b))，并使用 hinge 损 失来评估其对数据的拟合程度，即

同时，样本 xi 距离超平面 w⊤x + b 的欧氏距离为

此时，如果要求对所有样本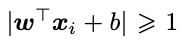成立，距离超平面的最小距离为∥w∥−1，那么支持向量机尝试最大化 ∥w∥−1。

具体来讲，支持向量机通过求解如下优化问题来获得分类器，即

其中，C 是参数，ξi 是松弛变量，用来处理数据不完全可分的情况(如数据噪声)。图 1.7 给出了支持向量机的示意图。

式 (1.19) 称为优化问题的主形式(primal form)，其等价的对偶形式(dual form)为

线性分类的局限在于当数据是非线性时，它们难以进行较好的分类。这种 情况下，一个常用方法是将数据点映射到一个高维空间，在这个高维空间中原 本线性不可分的样本点变得线性可分。但是，由于在高维空间中计算内积比较困难，学习过程将变得很慢甚至不可行。

值得庆幸的是，核函数可以帮助解决这个问题。由核函数代表的特征空间 称为再生核希尔伯特空间(Reproducing Kernel Hilbert Space，RKHS)，而此 空间上的内积等于原空间上内积的核映射。换言之，对所有 xi，有

其中 φ 是从原空间到高维空间的映射，K 为核函数。基于此，可以将对偶问题(1.20) 中的内积替换为核函数。

根据 Mercer 定理 [Cristianini & Shawe-Taylor，2000]，每个半正定对称函数都是核函数。常用的核函数包括线性核

其中 σ 为高斯核的宽度。

核技巧 (kernel trick)，即通过核函数将数据点映射到 RKHS 完成学习的方法，是一种常用的学习策略，可以和任何考虑输入空间内积的学习方法配合 使用。当使用核技巧后，相应的学习方法称为核方法。不难发现，支持向量机是 一类特殊的核方法，即使用核技巧的线性分类器。

评估和对比

通常，我们需要从多个学习算法中挑选合适的学习算法，或者选择合适的 参数。挑选最优算法和参数的任务称为模型选择，为此需要估计学习器的效果。基于实验方法，这需要设计一系列的实验并通过假设检验来比较不同的模型。

显然，使用学习器在训练集上的误差，即训练误差，来评估学习器的泛化 性能是不合适的，这是因为训练误差会偏好复杂模型而非具有较好泛化能力的 模型。通常，一个高度复杂的学习器，如完全生长的决策树，具有很低的训练误 差，但会有过拟合问题，从而在未见样本上表现较差。此时，合理的学习性能评 估过程应该在验证集上进行。需要注意的是，在训练过程中，训练集和验证集 的类别标记都是已知的，当模型选定后，应该共同使用这些数据来获得最终的 学习器。

事实上，我们常把一个数据集划分成两部分来获得训练集和验证集。当进 行数据集划分时，应该尽量保留原始数据的各种性质，否则验证集很可能会产 生误导性结果。举一个极端的例子，如果训练集仅包含正样本，验证集仅包含 负样本，这显然是不合适的。在分类问题中，如果要随机划分原始数据集，应该 保持训练集和验证集具有相似的类别比例;这种保留类别比例的采样方式通常 称为分层采样。

如果没有足够的标记数据来获得一个独立的验证集，一个常用的验证方法是交叉验证(cross-validation)。在 k 折交叉验证中，原始数据集 D 首先被分层划分成 k 个相同大小的互斥子集 D1,...,Dk，然后执行 k 次训练-测试过程。在第 i 次执行中，使用 Di 作为验证集，并使用其他所有子集(即)作j=i为训练集。最终返回 k 个测试结果的均值作为交叉验证的结果。为了降低划分 数据时随机性带来的影响，k 折交叉验证通常需要使用不同的随机划分重复 t次，即 t 次 k 折交叉验证。常用的实验配置包括 10 次 10 折交叉验证，以及Dietterich [1998] 建议使用的 5 次 2 折交叉验证。当 k 等于原始数据集中的样本 数量时，验证集仅包含一个样本，这种方法就是留一法(leave-one-out)验证。

基于估计误差可以比较不同的学习算法。由于数据划分具有一定的随机性， 简单地比较平均误差可能并不可靠。为此，通常使用假设检验。

若学习算法可高效执行 10 次，5 次 2 折交叉验证成对 t 检验是一个好的 选择 [Dietterich，1998]。该检验首先执行 5 次 2 折交叉验证。在每次的 2 折交 叉验证中，数据集 D 被随机划分为相同大小的 D1 和 D2 两个子集，两个算法a 和 b 分别在一个子集上训练并在另一个子集上测试，从而获得四个误差估计:

将服从自由度为 5 的 Student’s t 分布。选定显著程度α，如果t落在区间[−t5(α/2), t5(α/2)] 内，将接受零假设，即表示两个算法没有显著差异。常用的 显著程度 α 包括 0.05 和 0.1。

若算法仅能被执行一次，可以使用 McNemar 检验 [Dietterich，1998]。用err01 表示第一个算法分类错误但第二个算法分类正确的样本数，err10 表示第一 个算法分类正确但第二个算法分类错误的样本数。如果两个算法具有相同的效 果，err01 应该和 err10 具有基本相同的值，因此，统计量服从χ2 -分布。

有时，需要在多个数据集上评估多个学习算法。在这种情况下，可以使用Friedman 检验 [Demšar，2006]。首先，基于平均误差，在每个数据集上对每个 算法排序，具有最小误差的最优算法排序值(rank)设为 1，其他算法依次获得 较大的排序值。然后，可以获得每个算法在所有数据集上的平均排序值，并用Nemenyi post-hoc 检验 [Demšar，2006] 来计算临界差(critical difference)值

其中 k 是算法数量，N 是数据集数量，qα 是临界值(critical value)[Demšar，2006]。如果两个算法的平均排序值的差大于临界差，那么它们的效果具有显著 差别。

如图 1.8 所示，Friedman 检验的结果可以用临界差图来展现;其中，每个 算法对应一条线段，线段的中点是该算法的平均排序值，线的宽度是临界差。在 图 1.8 中，在该显著程度下，算法 A 显著优于其他算法，算法 D 显著劣于其他 算法，算法 B 和 C 没有显著差别。

集成学习方法

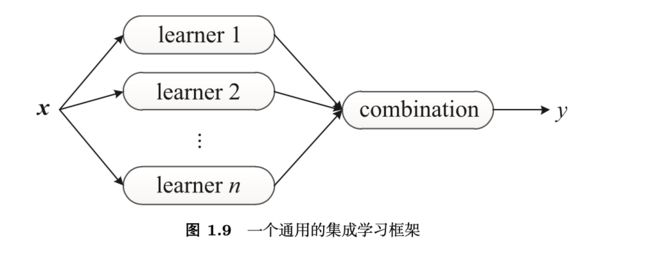
和传统学习方法训练一个学习器不同，集成学习方法训练多个学习器 并结合它们来解决一个问题。通常，集成学习也被称为基于委员会的学习(committee-based learning)或多分类器系统(multiple classifier system)。图 1.9 给出了一个通用的集成学习框架。一个集成由多个基学习器(base learner)构成，而基学习器由基学习算法(base learning algorithm)在训练数据上训练获得，它们可以是决策树、神经网络或其他学习算法。

大多数集成学习方法使用同一种基学习算法产生同质的基学习器，即相同种类的学习器，生成同质集成(homogeneous ensemble)；同时，也有一些方法使用多种学习算法 训练不同种类的学习器，构建异质集成(heterogeneous ensemble)。在异质集 成中，由于没有单一的基学习算法，相较于基学习器，人们更倾向于称这些学 习器为个体学习器(individual learner)或组件学习器(component learner)。

通常，集成具有比基学习器更强的泛化能力。实际上，集成学习方法之所以 那么受关注，很大程度上是因为它们能够把比随机猜测稍好的弱学习器(weak learner)变成可以精确预测的强学习器(strong learner)。因此，在集成学习 中基学习器也称为弱学习器。

由于使用多个模型解决问题的思想在人类社会中有悠久的历史，我们难以 对集成学习方法的历史进行溯源。例如，作为科学研究的基本假设，当简单假 设和复杂假设都符合经验观测时，奥卡姆剃刀(Occam’s razor)准则偏好简单 假设;但早在此之前，希腊哲学家伊壁鸠鲁(Epicurus，公元前 341—270)提 出的多释准则(principle of multiple explanations)[Asmis，1984] 主张应该保 留和经验观测符合的多个假设。

集成学习领域的发展得益于三个方面的早期研究，即:分类器结合、弱分类器集成和混合专家模型(mixture of experts)。分类器结合主要来自模式识别 领域。这方面的研究关注强分类器，试图设计强大的结合规则来获取更强的结 合分类器，在设计和使用不同的结合规则上积累深厚。弱分类器集成方面的研究主要集中在机器学习领域。这方面的研究关注弱分类器，试图设计强大的算法提升弱分类器的效果，产生了包括AdaBoost 和 Bagging 等众多著名的集成学习算法，并且在将弱学习器提升为强学习器方面有深入的理论理解。混合专家模型的研究主要集中在神经网络领域。在此，人们通常考虑使用分而治之的策略来共同学习一组模型，并结合使用它们获得一个总体解决方案。

20 世纪 90 年代以来，集成学习方法逐渐成为一个主要的学习范式，这主 要得益于两项先驱性工作。其中，[Hansen & Salamon，1990] 是实验方面的工 作, 如图 1.10 所示，它指出一组分类器的集成经常会产出比其中最优个体分类 器更精准的预测;[Schapire，1990] 是理论方面的工作，它构造性地证明了弱学 习器可以被提升为强学习器。虽然我们所需的高精度学习器难以训练，但弱学 习器在实践中却容易获得，这个理论结果为使用集成学习方法获得强学习器指明了方向。

一般来讲，构建集成有两个步骤:首先产生基学习器，然后将它们结合起 来。为了获得一个好的集成，通常认为每个基学习器应该尽可能准确，同时尽可能不同。

值得一提的是，构建一个集成的计算代价未必会显著高于构建单一学习器。这是因为使用单一学习器时，模型选择和调参经常会产生多个版本的模型，这 与在集成学习中构建多个基学习器的代价是相当的;同时，由于结合策略一般 比较简单，结合多个基学习器通常只会花费很低的计算代价。

集成学习方法的应用

KDD Cup 作为最著名的数据挖掘竞赛，自 1997 年以来每年举办，吸引了全球大量数据挖掘队伍参加。竞赛包含多种多样的实际任务，如网络入侵检测(1999)、分子生物活性和蛋白质位点预测(2001)、肺栓塞检测(2006)、客户 关系管理(2009)、教育数据挖掘(2010)和音乐推荐(2011)等。在诸多机器 学习技术中，集成学习方法获得了高度的关注和广泛的使用。例如，在连续三 年的 KDD Cup 竞赛中(2009—2011)，获奖的冠军和亚军都使用了集成学习方法。

另一项著名的赛事 Netflix Prize由 Netflix 公司举办。竞赛任务是基于用 户的历史偏好提升电影推荐的准确度，如果参赛队伍能在 Netflix 公司自己的算 法基础上提升 10% 的准确度，就能够获取百万美元大奖。2009 年 9 月 21 日，Nexflix 公司宣布，百万美元大奖由 BellKor’s Pragmatic Chaos 队获得，他们的 方案结合了因子模型、回归模型、玻尔兹曼机、矩阵分解、k-近邻等多种模型。另外还有一支队伍取得了和获奖队伍相同的效果，但由于提交结果晚了 20 分钟 无缘大奖，他们同样使用了集成学习方法，甚至使用“The Ensemble”作为队名。

除了在竞赛上获得显赫战绩，集成学习方法还被成功应用到多种实际应用 中。实际上，在几乎所有的机器学习应用场景中都能发现它的身影。例如，计算 机视觉的绝大部分分支，如目标检测、识别、跟踪，都从集成学习方法中受益。

基于 AdaBoost 和级联结构，Viola & Jones [2001，2004] 提出了一套通用 的目标检测框架。Viola & Jones [2004] 显示在一台 466MHz 计算机上，人脸检 测器仅需 0.067 秒就可以处理 384×288 的图像，这几乎比当时最好的技术快 15倍，且具有基本相同的检测精度。在随后的十年间，这个框架被公认为计算机 视觉领域最重大的技术突破。

Huang et al. [2000] 设计了一套集成学习方法解决姿态无关的人脸识别问 题。它的基本思路是使用特殊设计的模型集成多个特定视角的神经网络模型。和需要姿态信息作为输入的传统方法相比，这个方法不需要姿态信息，甚至能 在输出识别结果的同时输出姿态信息。Huang et al. [2000] 发现这个方法的效果 甚至优于以完美姿态信息作为输入的传统方法。类似的方法后来被用于解决多 视图人脸检测问题 [Li et al.，2001]。

目标跟踪的目的是在视频的连续帧中对目标对象进行连续标记。通过把目 标检测看成二分类问题，并训练一个在线集成来区分目标对象和背景，Avidan [2007] 提出了集成跟踪(ensemble tracking)方法。该方法通过更新弱分类器来学习由于对象外观和背景发生的变化。Avidan [2007] 发现这套方法能处理多种 具有不同大小目标的不同类别视频，并且运行高效，能应用于在线任务。

在计算机系统中，用户行为会有不同的抽象层级，相关信息也会来自多个 渠道，集成学习方法就非常适合于刻画计算机安全问题 [Corona et al.，[2009]。Giacinto et al. [2003] 使用集成学习方法解决入侵检测问题。考虑到有多种特征 刻画网络连接，他们为每一种特征构建了一个集成，并将这些集成的输出结合 起来作为最终结果。Giacinto et al. [2003] 发现在检测未知类型的攻击时，集成 学习方法能够获得最优的性能。此后，Giacinto et al. [2008] 提出了一种集成方 法解决基于异常的入侵检测问题，该方法能够检测出未知类型的入侵。

恶意代码基本上可以分为三类:病毒、蠕虫和木马。通过给代码一个合适 的表示，Schultz et al. [2001] 提出了一种集成学习方法用以自动检测以往未见 的恶意代码。基于对代码的 n-gram 表示，Kolter & Maloof [2006] 发现增强决 策树(boosted decision tree)能够获得最优的检测效果，同时他们表示这种方法可以在操作系统中检测未知类型的恶意代码。

集成学习方法还被应用于解决计算机辅助医疗诊断中的多种任务，尤其用 于提升诊断的可靠性。周志华等人设计了一种双层集成架构用于肺癌细胞检测 任务 [Zhou et al.，2002a]，其中当且仅当第一层中的所有个体学习器都诊断为“良性”时才会预测为“良性”，否则第二层会在“良性”和各种不同的癌症类 型间进行预测。他们发现双层集成方法能同时获得高检出率和低假阳性率。

对于老年痴呆症的早期诊断，以往的方法通常仅考虑来自脑电波的单信道数据。Polikar et al. [2008] 提出了一种集成学习方法来利用多信道数据;在此方法中，个体学习器基于来自不同电极、不同刺激和不同频率的数据进行训练，同时它 们的输出被结合起来产生最终预测结果。

除了计算机视觉、安全和辅助诊断，集成学习方法还被应用到多个其他 领域和任务中。例如，信用卡欺诈检测 [Chan et al.，1999;Panigrahi et al.，2009]，破产预测 [West et al.，2005]，蛋白质结构分类 [Tan et al.，2003;Shen & Chou，2006]，种群分布预测 [Araújo & New，2007]，天气预报 [Maqsood et al.，2004;Gneiting & Raftery，2005]，电力负载预测 [Taylor & Buizza，2002]， 航空发动机缺陷检测 [Goebel et al.，2000;Yan & Xue，2008]，音乐风格和艺 术家识别 [Bergstra et al.，2006] 等。

---

 赠书活动 

想要了解关于集成学习的更多干货知识，关注AI科技大本营并在评论区分享你对本文的学习心得或集成学习的见解，我们将从中选出10条优质评论，各送出《集成学习：基础与算法》一本。

▼ 扫码或点击阅读原文获取本书详情 ▼