上一篇:数学思想方法揭秘-7(原创)。回前言。
最小维度思想
这个思想其它书籍上没有提到,关系思想也是这样,但我们自己可以总结提炼出来,不必拘泥于书本。
最小维度思想类似公理化思想,小初高学习的欧式几何就建立在少数几条公理和公设基础上。最小维度,体现了最简思维,运用减法、简化精简、抽象,去粗取精,在深入分析事物之间的联系基础上,做减法,剥离非本质的因素,保留原始朴素的、母性的、公共的、基础底层的、奠基性的本质元素,把这些本质元素作为基础维度和对象,即基底或基元,其它对象可用基底来表示。和特斯拉CEO马斯克的第一性原理(First Principle)也有些许关系。这里引用马斯克对第一性原理的描述:
我在想存在一种好的思维框架。那是物理学的东西,你知道,有点儿像第一原理推理(first principles reasoning)。总体来讲,我认为存在将事情缩减至其根本实质……你必须能够把那些问题“煮沸蒸馏”才能从里面找出那些最基本的东西,再从这些最本质最基本的东西开始进行推理。
我确实认为有一个很好的思考框架。这是物理学。您知道,这是第一类原则推理。总的来说,我认为是这样-我的意思是将事物简化为基本事实并从那里进行推理,而不是通过类比推理。
在我们一生的大部分时间里,我们都是通过类比推理来度过人生,这实质上意味着模仿别人所做的微小变化。
这里有对第一性原理更深入的解释 :第一性原理、第一性原理三步思考法。
最小维度思想,先介绍和它有关联的维度思想,维度思想就是通过发散思维,从多个维度多个视角全面系统地看问题、去探索解决方案、去寻找可能的变化点,变化点也是机会点突破点。
最小维度思想就是一种降维,利用维度之间的关系,降低问题的维度,例如x+y+z是3维3个变量,如果已知条件中y和z存在关系,例如z=2y,或我们通过已知条件推理出y和z的关系,那我们就可以将x+y+z变为x+3y,这样就降为两维了,维度减少通常会简化问题,降低问题复杂度,不过也不绝对,有时要升维,要具体问题具体分析,辩证的来看,不能死板机械。
最小维度思想体现简洁之美,就是找出刻划一个事物或对研究对象建模需要的最少维度或最少的变量(或影响因素),例如在我们生活的空间中,确定一个点的位置,只要3个维度就可以了,不多不少。
系统内部各组成部分之间是相互联系相互依赖的,如果要对它们之间的关系进行研究,进行刻画和建模,我们一般从关系结构中筛选出最本质最基础最底层、起决定性作用的一些必要对象、对象属性或参数,以这些做基础来建立我们的关系结构模型,确定了这些基础的核心的东西,要研究的整个系统就能确定下来了,这就是最小维度思想,提纲挈领,这也是矛盾论中提到的抓主要矛盾和矛盾的主要方面。一个三维物体的结构,通常确定了长宽高三个维度的数据就能确定这个物体,这些是必要的,其他的数据可以基于这些基础数据来推算来衍生,这些基础数据就是根。
一道数学题也是一个系统,题目中的对象之间也存在各种关系,我们在解题时要识别哪些是本质基础的对象及其对象属性,确定之后就可基于它们来展开解题研究。例如确定一个直角三角形的大小和面积,我们只需要知道两个参数即可:两条直角边长度或一条斜边和一条直角边或一条边和其中一个锐角或斜边与高;列方程,我们只选取必要的少数变量做未知数,其他对象可以基于这些未知数来描述和表达。
降维作为一种数学方法,正体现了最小维度思想,一般情况下高维&变量多通常比低维&变量少的要复杂些,例如一个代数式或方程组中有3个变量(未知数)的通常比2个变量的要复杂,2个的比1个的要复杂,所以我们在解题时碰到多维多变量的问题要试着去减少变量的个数,或减少次要的变量,保留对问题起决定作用的核心关键变量,或用合适的基础变量或独立变量来表示其他变量,例如,这里就是基础变量(基底)。这样就可简化问题,看清问题。
方程、不等式中的消元法就属于降维,它也体现了最小维度思想,当然也体现了'转化'思想(多元方程转化成少元方程),指数降次也是另一种形式的降维,在多变量不等式解题中也能看到最小维度思想的运用。
高中阶段圆锥曲线的参数方程,也体现了最小维度思想。
最小维度思想中的降维不只是减少变量或未知数的数量,有时体现在减少变化点的数量,例如对分式
这个分式虽然只有一个变量,但分子、分母都出现了变量,分子、分母都是变化的,也就是有两个变化点。变化点多,且这些变化点通常存在各种联系,不是独立变化的,也就容易相互牵扯、相互影响、相互耦合,关系复杂不便于处理,所以我们将该分式变形为。这样就减少为只有一个变化点或者说我们把变化集中在少数几个地方而不是分散在多处,也就是只有分母可变。显然减少了变化点之后,很容易看清,很容易得出结论,分式是递增的。当然也可以把变化点作为维度,减少变化点就是降维。有时我们对代数式按某个标准进行某种分组变形、进行分与合,例如把代数式的常数和变数分离,或合并同类项,也大体可理解为按某个标准进行降维或解耦或归并。
第48题
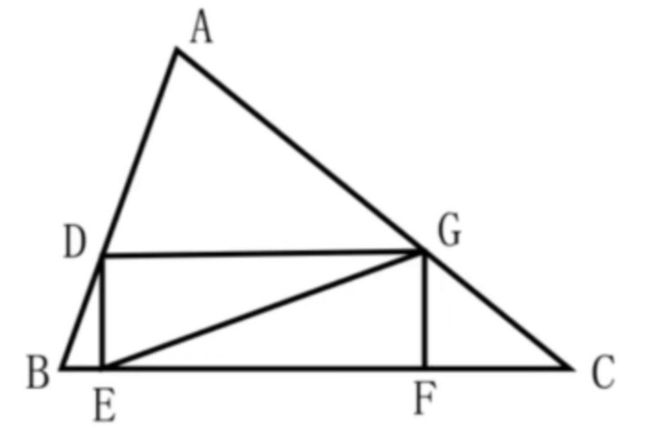
在ABC中,BC=6,BC边上的高为4,在三角形内部作一个矩形EFGD,EF在BC边上,另外两个顶点D、G分别在AB和AC上,求对角线EG的最小值。
显然可以有很多个不同的矩形,此题求这些矩形对角线的最小值。先不管最小值,我们将题目转化成求对角线的长度表达式,也即是对角线长度函数解析式,再求出这个函数的最小值。
求对角线的函数表达式,需要确定矩形的位置和大小,根据题目的已知条件,我们可得出只要知道DG的长度或DG与BC的比值或ADG中DG边上的高之后,即可确定矩形位置和长、宽、对角线,这就是运用了最小维度思想。
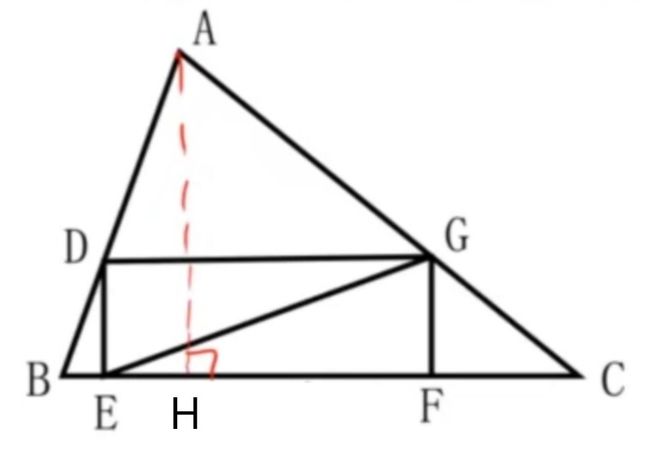
对此题,我们作高AH,设。根据已知条件、平行线的比例关系,最终可得出对角线EG长度的函数表达式,为的一元二次函数,根据这个函数即可求出最小值。此处就体现了最小维度思想,找出最小维度,这题结合已知条件,只要一个变量一个维度就足以解决问题,即,用一个变量(一维)x就足够了。
第49题(高中)
已知a、b为正数,且a不等于b,证明:
这题是对数均值不等式,我们证明等式左边部分,右边部分类似。
总结:分析法、变形转化、构造法(构造出函数g(x))、最小维度思想。此题有两个变量a和b,是两维或二元不等式,但我们通过变形转化,将其降维改造成一维一元,就是上面的函数g(x)。这题也能体现归一化无量纲思想和比例思想、单位一思想。
第50题(高中)
这题也是运用了最小维度思想,逐步消除最小值代数式中的变量a和b,最后保留核心基础的独立的变量c,减少了变量个数,简化了问题,便于解决问题。
思维过程和解题方法见下图。观察题目中的变量,可以发现a与b联系相对紧密(体现在a+b=2关系中),代数式中c和a、b基本上没有联系,它相对孤立独立和特殊,它其实是这个代数式中的主角,关键的对象,起决定作用的对象。这题多体会联系与孤立/隔离的辩证关系。
总结:这道题运用了观察、比较评估(在考虑要消除哪些变量时,根据题目的实际情况进行比较评估和分析,选取了a、b两个变量作为要消除的变量,保留c这个独立的核心的特殊的变量,要消除c是不可行的,只能是保留它)、最小维度思想。
类似的题:已知。自己思考下。
思考.........................................................................................................
.................................................................................................................
.................................................................................................................
.................................................................................................................
................................................................................................................
这题应用最小维度思想,首先要确定消除最小值代数式中的哪个或哪些变量。
思考-----------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
观察题目特征,可以发现c比较特殊,所以要想法消除a和b,具体怎么消除?
思考------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------
根据代数式中的2ab,和已知条件三个变量的平方和为1,把这些信息(数据)联系结合在一起考察分析,就启发我们联想到基本不等式,也就是=,利用好三个变量的平方和为1,此处就是,可见我们可以消除最小值式子中的a和b两个变量,只剩下一个c:,等号成立时,a=b,c=,尽验证符合题目已知条件和约束,所以最小值为4。最后一步用到基本不等式。
此外这题的思维活动也多多少少涉及到心理学和认识论中的同化和顺应。在这道题中,我们的最小值代数式顺应已知条件,对这个最小值代数式进行改造&变形&调整来顺应迁就靠近这个平方和为1的已知条件,可以理解为对代数式中的矛盾和复杂性(多维多元的结构形式)进行了改造转化,达到同化的目的,这样经过同化之后就利用好&利用上了已知条件。顺应前面也讲过,在解题中就是根据题目中的各种特征和形势,结合自己的知识结构和经验,因地制宜、依形就势、扬长避短,对题目中矛盾的复杂的因素进行改造&调整&转化&重构&扩张&重组,最终同化到一些已知条件和知识&规律上来,达到新的平衡与和谐。同化和顺应在每道题的解题思维过程和平时的学习过程中都有发生,要多加体会。
第51题 (高中)
已知为正数,且。证明。
方法之一,通过观察,
ab应和ac组合,bc和abc组合。因为ab和ac组合后变成a(b+c),而b+c=1-a,这样就减少了变量的数量。
而bc和-abc的组合,产生bc(1-a),而bc和b+c有关系(联系)【】,b+c和a有关系,这样bc和a之间就产生或建立了关系,有关系之后,那它们之间就可能会存在我们需要的单向或双向的转化或过渡。这里也看到数学解题中关系思想无处不在,知道关系的重要性,关系是转化变化的桥梁纽带。
发现、寻找、联想相同或同类或相似相近的对象、关系或找相似度高的对象和关系,利用它们之间的这种相同或相似的联系,例如进行等量代换、换元、转化、逼近等。ab+ac组合后变成a(b+c),这里的b+c和已知条件a+b+c=1中的b+c相同,a(b+c)和a+b+c=1存在局部相同的对象。
又=
= ,
=
这道题有三个变量,运用最小维度思想,我们将3个变量降为1个变量,在降维中也隐含有"逼近思想",从最初三个变量的形式一步步变形(通过等量代换和放缩:,,消除了bc),向一个变量的形式(最终目标)靠近。在逼近的过程中我们要根据题目的特征和下一步设想的目标意图&需要,发散思维,联想学过的知识点,运用它们来实现设想的目标。例如在这一步,我们合理设想下一步的目标是消除bc或b、c两个变量,或者说需要消除bc,所以我们结合bc是相乘的结构特征,且有,所以联想到这个知识点,从而利用它来消除bc。
下一篇:数学思想方法揭秘-9(原创)。