17.立体匹配——动态规划公式（Dynamic Programming Formulation），二维网格上的相干立体_4

目录

动态规划公式（Dynamic Programming Formulation）

二维网格上的相干立体

---

动态规划公式（Dynamic Programming Formulation）

这就是所谓的动态规划公式。这有点复杂，但请耐心听我说。

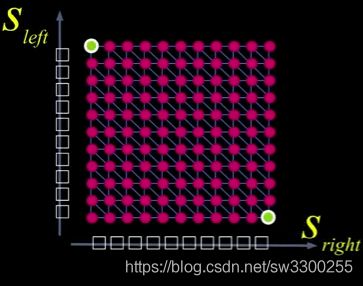
我们这里有，我假设我有左边的扫描线信号在这里每一个都是像素（如图1）。不过，我注意到点比像素多。假设这个网格中有多少个点就有多少个正方形。这里也是一样（如图2）。

1  2

假设我们知道这里最左边的像素对应这个（如图1）。最右边的像素对应于这个，all right?

1 2

那么，从左到右的映射的一个解就是从左上角到右下角的路径。有一条特定的路径（如图1），okay? 目标是找到可能的最佳路径。最好的路径意味着最低的成本。

1 

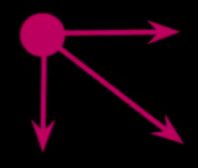
现在，当你位于这个网格中的某个地方（如图），这个地方只有三种不同方向的路径可以走。

最简单的方法是沿着对角线走（如图）。

现在，当你沿着对角线走，它的意思是，如果这个像素（X轴）映射到这（Y轴）个，那么这个（X轴）就映射到下一个（Y轴）。也就是说，它们保持相同的差异。如果我要加3来匹配这个像素，那么这个也是加3，然后继续。

1

2

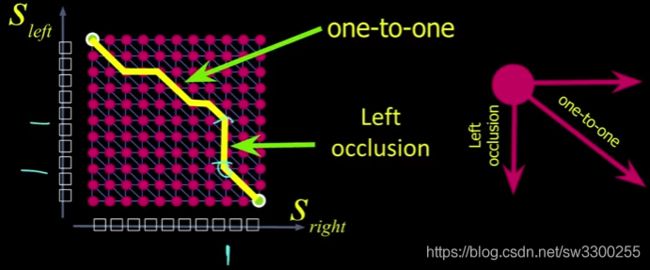
但是，假设我有一些像素在一个图像中可见，在下一个图像中不可见。这里有一个，我说的区域是左遮蔽（occlusion）。我的意思是左眼看得见，右眼看不到。这意味着所有这些像素（如图1），这个范围（如图2），都映射到这个位置（如图3）。

12

3

你可以把它想象成这个像素（如图1）被映射到这个像素上（如图2），但是所有这些都没有被看到（如图3）。这就是左遮蔽（Left Occlusion）。

 12

3

相应地，你可以有右遮蔽（如图），all right?

我们的目标是找到成本最低的方法。现在，当你对角线移动时，你的成本就是两个像素之间的匹配，这个匹配和我们之前做的很像。归一化相关性或平方差的和，取决于你做的是相似还是不相似的。但是当你不是一对一的时候，你实际上是在做遮蔽（Occlusion），你需要做的是为遮蔽像素付出代价。设计了很多方法告诉你如何分配成本。有些他们是贝叶斯定理，有些是其它的。 

现在，对于那些知道最短路径或者Dijkstra算法或者其他求解方法的人。这可以表示为一个动态规划问题。动态规划方法很好，因为它们计算效率高。你不需要计算所有可能的路径。但你仍然可以计算出可能的最佳路径。唯一需要的是你必须能够计算水平的，垂直的 或 对角线的成本。在这里，我列出了一些参考资料，包括博斯克(Bobick)的一篇，它展示了如何做到这一点。我们介绍了这个叫做地面控制点（ground control points）的东西，这是一种很酷的方式对你使用的遮蔽成本值不是很敏感。这是早期方法的一部分问题，但这是在后面的。

二维网格上的相干立体

再看看斯库巴大学的事情，这里你可以看到，通过动态编程，我们得到了比以前更好的解决方案。这里的情况越来越好，那里也越来越好（如图）。但是你会注意到这些条纹。这是有意义的因为每条扫描线都是独立于另一条扫描线的。所以它不知道之前的解，所以当你改变扫描线，你可能会得到一个合理的位移。不幸的是，你不能用动态规划在二维网格上找到空间上一致的差异集。你必须采取另一种方法。

所以在激励另一种方法时，我们这样想的，是什么定义了一组好的对应（correspondences）? 首先，回到我们之前的工作。我们希望每个像素从左到右找到一个好的外观匹配。或者从右到左。我们讨论匹配质量。但另一件事是，还记得我们第一次过滤噪音的时候，我们说过我们做的一个假设是附近的两个像素有相似的实值吗? 当你谈到深度的时候，你也可以讨论附近的两个像素是如何有接近相同深度的趋势的。这意味着它们可能有相同的差异。所以，如果这个像素，需要平移4个单位，那么附近的这个就不应该平移很多。okay，我可能想惩罚那些有很多跳跃的解。

我们现在要用的方法是：我们先来看这两个东西（如图），它把立体视觉看作是能量最小化的问题。第一项，能量迷你，哦，让我。我应该在这里定义i1是左边的图像，i2是右边的图像。我们在左边有一个窗口，我们要从右边看它，然后一直到右边是一个视差图像，okay? 这就是我们计算的视差。

我们的能量最小化方法需要两个能量项。第一项是数据项（如图1）。数据项表示对所有像素求和（如图2），这个窗口（如图3）减去来自另一个图像上的窗口（如图4），所以这个窗口（如图5）减去那个这个窗口（如图6）的平方（如图7），应该尽可能小。所以，我们想，如果我们要做能量最小化我们的数据项，基本上是看的是平方差。 这和我们之前做的很相似。一种考虑方法是，当我们通过den搜索进行匹配时，我们只看数据项。

1

2

3

4

5

6

7

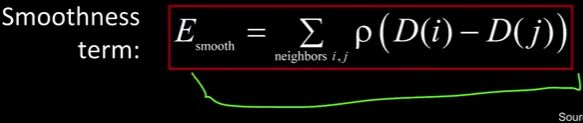
第二项叫做平滑项（如图1）。你会注意到这里没有任何窗口，这里没有任何窗口，我只是看着这里的窗口（如图2）。事实上，在平滑项中，图像根本不在这里（如图3），无论是左边还是右边。我只看到了视差图像中邻居（如图5）的窗户（如图4），这是视差图像，all right。

1

2

3

4

5

这个行函数，这个函数本质上是一个鲁棒范数（robust norm）。所以你想要的是，做少量的改变是可以的，然后当你变得昂贵时，做大的改变，但是做更大的改变不应该变得更昂贵。因为这是一种辅助编辑遮蔽（adjunct edit occlusion）。所以这个行函数是稳健的。我的意思是，你可以把它看成一个平方，这个，这个，这个的最大值。但这是我们的平滑项。

对于能量最小化，我们要做的是我们有一个总能量它是数据项的混合（如图1），平滑项（如图2）由这些系数（如图3）进行加权。你想要找到的，这是困难的部分，你想要找到一个分配差异的方法来最小化这个能量函数。

1

2

3

---

编程之久除了算法和数据结构，什么也不属于我们。