Python学习笔记-计算思维

Python学习笔记-计算思维

以体育竞技分析为例，IPO如下：

• 输入：另个球员（A，B）的能力值，模拟比赛场次
• 处理：模拟比赛过程
• 输出：球员A和B分别赢得比赛的概

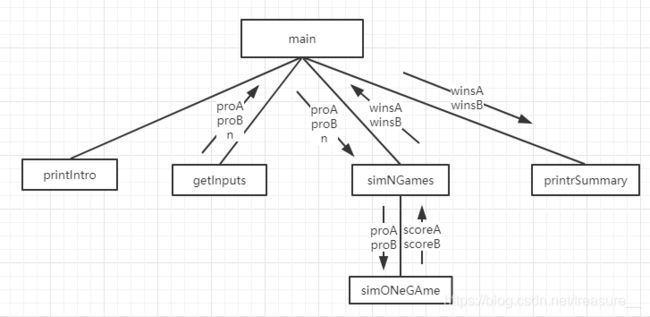
自顶向下的设计

 

设计步骤：

1. 将算法表达为一系列小问题
2. 为每个小问题设计接口
3. 通过将算法表达为接口关联的多个小问题来细化算法
4. 为每个小问题重复上述过程

#matchSim.py     
from random import random#引入random库中的random函数
def simOneGame(proA,proB):#模拟每次比赛，若是A胜则A先拿到15分，即scoreA=15>screB
    serving="A"#设第一场发球方为A
    scoreA=scoreB=0#初始化每场A,B的分数
    while not scoreA==15 or scoreB==15:#若A或B任意一方先拿到15分，即获胜，同时停止比赛；不然比赛就一直继续
         if serving=="A":#若发球方为A
            if random()screB
        if scoreA>scoreB:
            winsA+=1.0#若A胜，则A的获胜次数就+1 
        else:
            winsB+=1.0#同上
    return winsA,winsB#模拟n次后，返回A,B的获胜次数，以待输出

def printSummary(winsA,winsB):#输出A，B获胜的比赛的次数及概率
    n=winsA+winsB
    print "\nGames simulated:%d"%n#输出模拟比赛的场次：n次
    a=winsA/n
    b=winsB/n
    print "Wins for A:{0}({1:0.1%})".format(winsA,a)
    #{1:0.1%}:格式化第而2个数，保留一位小数，右对齐，以0作为补充。
    print "Wins for B:{0}({1:0.1%})".format(winsB,b)
    #输出B获胜次数，及概率
    

if  __name__=='__main__':main()
#一般用来测试模块功能的，只有直接运行［python 模块.py］的时候才会运行这个

原型开发（螺旋式开发）

基本思想：从一个简单的程序或者一个程序组件开始，逐渐添加特性，直到其完全，满足要求。即首先设计、执行原型，然后再设计、执行并测试新特征，再将原型逐步扩展为最终的程序，在整个程序发展周期上通过设置很多小的环形结构改善程序功能。

基于原型的改善计划：

1. 最初的原型。进行30回合的比赛，发球方始终有50%的概率得分，在每一次发球后输出比分。
2. 添加两个参数代表两个球员的能力值（赢球的概率）。
3. 进行比赛直到一个球员达到15分。此时，拥有了一场单一比赛的模拟信息。
4. 将比赛扩展为多场比赛，输出每个球员赢得的比赛次数。
5. 建立完整的程序，添加交互输出和格式化报告。

#matchSim_1.py
from random import random
def simOneGame():
    scoreA=0
    scoreB=0#初始化双方得分
    serving="A"#设第一次的发球方为A
    for i in range(30):#进行30回合的比赛
        if serving=="A":
            if random()<.5:#发球方始终有50%的胜率
                scoreA+=1
            else:
                serving="B"
        else:
            if random()<.5:
                scoreB+=1
            else:#失败后，转换发球方
                serving="A"
        print scoreA,scoreB#输出比分
simOneGame()

  

#matchSim_2.py
from random import random
def simOneGame(proA,proB):
    scoreA=0
    scoreB=0#初始化双方得分
    serving="A"#设第一次的发球方为A
    for i in range(30):#进行30回合的比赛
        if serving=="A":
            if random()

#matchSim_3.py
from random import random
def simOneGame(proA,proB):
    scoreA=0
    scoreB=0#初始化双方得分
    serving="A"#设第一次的发球方为A
    while not gameOver(scoreA,scoreB):#若有A或B任意一方先拿到15分则立即停止本场比赛
        if serving=="A":
            if random()

#matchSim_4.py
from random import random
def simOneGame(proA,proB):
    scoreA=0
    scoreB=0#初始化双方得分
    serving="A"#设第一次的发球方为A
    while not gameOver(scoreA,scoreB):#若有A或B任意一方先拿到15分则立即停止本场比赛
        if serving=="A":
            if random()screB
        if scoreA>scoreB:
            winsA+=1.0#若A胜，则A的获胜次数就+1 
        else:
            winsB+=1.0#同上
    print winsA,winsB#输出每个球员赢得的比赛次数
    return winsA,winsB#模拟n次后，返回A,B的获胜次数，以待输出
simNGames(500,0.5,0.5)
    

#matchSim_5.py
from random import random
def simOneGame(proA,proB):
    scoreA=0
    scoreB=0#初始化双方得分
    serving="A"#设第一次的发球方为A
    while not gameOver(scoreA,scoreB):#若有A或B任意一方先拿到15分则立即停止本场比赛
        if serving=="A":
            if random()screB
        if scoreA>scoreB:
            winsA+=1.0#若A胜，则A的获胜次数就+1 
        else:
            winsB+=1.0#同上
    return winsA,winsB#模拟n次后，返回A,B的获胜次数，以待输出
def main():
    print"The program simulates a game between two"
    print"There are two players,A and B"
    print"Probability(a number between 0and 1)is used"#打印比赛的介绍性信息
    #获得运行需要的参数：A,B的能力值，模拟比赛场次
    proA=eval(raw_input("What is the prob,player A wins?"))#获取A的能力值
    proB=eval(raw_input("What is the prob,player B wins?"))#获取B的能力值
    n=eval(raw_input("How many games to simulate?"))#获取模拟比赛场次
    winsA,winsB=simNGames(n,proA,proB)#模拟比赛过程
    n=winsA+winsB
    #输出比赛结果及概率
    print "\nGames simulated:%d"%n#输出模拟比赛的场次：n次
    print "Wins for A:{0}({1:0>1}%)".format(winsA,winsA/n*100)
    print "Wins for B:{0}({1:0>1}%)".format(winsB,winsB/n*100)

main()

以上代码，按照1-5的顺序即为原型开发体育竞技分析的过程。

螺旋式设计方法在处理新的或者不熟悉的特性或技术时及其有效，有助于用最少的代价实现程序的核心功能。

螺旋式开发与自顶向下的设计方式是互补的。