直方图均衡化原理及其python代码实现
如果一副图像的像素占有很多的灰度级而且分布均匀,那么这样的图像往往有高对比度和多变的灰度色调。直方图均衡化就是一种能仅靠输入图像直方图信息自动达到这种效果的变换函数。它的基本思想是对图像中像素个数多的灰度级进行展宽,而对图像中像素个数少的灰度进行压缩,从而扩展像原取值的动态范围,提高了对比度和灰度色调的变化,使图像更加清晰。
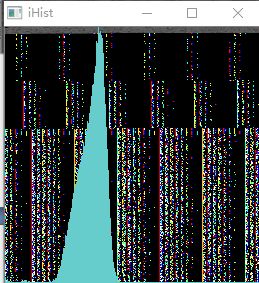
如下图1为退火后的430不锈钢金相组织的灰度图,图2为该图片的直方图,直方图主要集中在暗部,而对应的灰度图看起来很暗,清晰柔和的图像的直方图灰度分布应该要比较均匀,在这里我们就对这个图像进行直方图均衡化。
图1 退火后的430不锈钢金相组织
图2 原金相组织图直方图
图3 原金相组织图累积分布
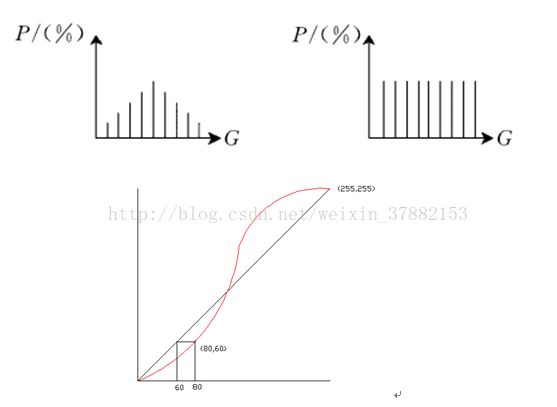
红色部分是原图累积分布函数轮廓线,而理想的均衡化累积分布函数轮廓线应该是一条斜线,对于原图中灰度值为80的点,按图中的方法我们把它转换为灰度值为60对每个灰度值,我们要寻找一个转换函数,对原图进行转换,就可以得到均衡化后的图了。
图3 均衡化示意图
设原始图像在(x,y)处的灰度为f,而改变后的图像为g,则对图像增强的方法可表述为:在(x,y)处的灰度f映射为g。在灰度直方图均衡化处理中对图像的映射函数可定义为:g= EQ (f),这个映射函数EQ(f)必须满足两个条件(其中L为图像的灰度级数):
(1)EQ(f)在0≤f≤L-1范围内是一个单值单增函数。这是为了保证增强处理没有打乱原始图像的灰度排列次序,原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列。
(2)对于0≤f≤L-1有0≤g≤L-1,这个条件保证了变换前后灰度值动态范围的一致性。
累积分布函数(cumulative distribution function,CDF)即可以满足上述两个条件,并且通过该函数可以完成将原图像f的分布转换成g的均匀分布。计算机离散系统的的直方图均衡化映射函数可表示为
:![]() (k=0, 1,2, …, L-1)
(k=0, 1,2, …, L-1)
其中,n是图像中像素的总和,是当前灰度级的像素个数,L是图像中可能的灰度级总数。
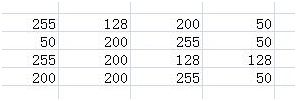
来看看通过上述公式怎样实现的拉伸。假设有如下图像:
得图像的统计信息如下图所示,并根据统计信息完成灰度值映射:
映射后的图像如下所示:
以上就是直方图映射均衡化的步骤,包括:
1)计算图像f(x,y)的各灰度级中像素出现的概率p(i);
2)计算p的累计概率函数s(k),s即为图像的累计归一化直方图;
3)将s(i)缩放至0~255范围内。
直方图均衡化就是把一已知灰度概率分布的图像经过一种变换使之演变成一幅具有均匀灰度概率分布的新图像,它是以累积分布函数变换法为基础的直方图修正法。
import cv2.cv as cv #需要OPENCV 2的版本 OPENCV 3的版本函数有些变化
def Hist(image,color =cv.RGB(102,204,204)): #获得原图像的直方图
a = [0]*256 #初始化256维向量,用于保存每个灰度级出现的次数
w = image.width
h = image.height
iHist = cv.CreateImage((256,256),8,3)
for i in range(h):
for j in range(w):
iGray = int(image[i,j]) #获得每个像素点的灰度级
a[iGray] = a[iGray] +1 #获得每个灰度级出现的次数
S = max(a)
print S
for k in range(256):
a[k] = a[k]*255/S
x = (k,255)
y = (k,255-a[k])
print y
cv.Line(iHist,x,y,color) #画出直方图(类似柱状图)---通过次数最多的归一化后
return iHist
def LHist(image,color =cv.RGB(102,204,204)): #获得累积分布图
a = [0]*256
w = image.width
h = image.height
iLHist = cv.CreateImage((256,256),8,3)
for i in range(h):
for j in range(w):
iGray = int(image[i,j])
a[iGray] = a[iGray] +1
for i in range(1,256):
a[i] = a[i]+a[i-1]
S = max(a)
print S
for k in range(256):
a[k] = a[k]*255/S
x = (k,255)
y= (k,255-a[k])
cv.Line(iLHist,x,y,color) #获得分布函数
return iLHist
def Equalize(image,color =cv.RGB(102,204,204)): #获得均衡化后的图像
a = [0]*256
w = image.width
h = image.height
size = (w,h)
iEqualize = cv.CreateImage(size,image.depth,1)
for i in range(h):
for j in range(w):
iGray = int(image[i,j])
a[iGray] = a[iGray] +1
for i in range(1,256):
a[i] = a[i]+a[i-1]
S = max(a)
print S
for k in range(256):
a[k] = a[k]*255/S
for i in range(h):
for j in range(w):
iEqualize[i,j] = a[int(image[i,j])]
return iEqualize
image = cv.LoadImage('org3.jpg',0)
iHist = Hist(image)
iLHist = LHist(image)
iEqualize = Equalize(image)
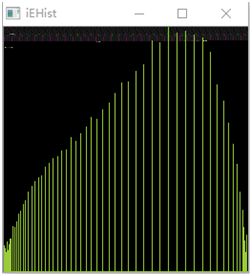
iEHist =Hist(iEqualize,cv.RGB(153,204,54)) #均衡化后的直方图
iELHist =LHist(iEqualize,cv.RGB(153,204,54)) #均衡化后的累积分布图
cv.ShowImage('image',image)
cv.ShowImage('iHist',iHist)
cv.ShowImage('iLHist',iLHist)
cv.ShowImage('iEqualize',iEqualize)
cv.ShowImage('iEHist',iEHist)
cv.ShowImage('iELHist',iELHist)
cv.WaitKey(0)
现在图像的直方图分布比较均匀了但很难得到完全均衡的结果,另外,变换后的灰度级减少了。这种现象叫做“简并”现象。由于简并现象的存在,处理后的灰度级总是要减少的直观反映就是均衡后直方图在垂直方向上有很多黑线。
直方图均衡化效果(左原图,右均衡化的图)