leetcode.动态规划专题
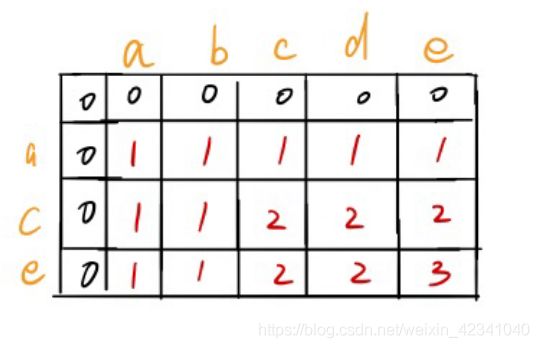
1143.Longest Common Subsequence(LCS)
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector<vector<int>>dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));//全初始化为0
for(int i = 1; i < text1.size() + 1; ++i){
for(int j = 1; j < text2.size() + 1; ++j){
if(text1[i - 1] == text2[j - 1]){
dp[i][j] = dp[i - 1][j -1] + 1;
}
else
dp[i][j] = max(dp[i][j -1], dp[i - 1][j]);//取二维矩阵左边和上边的最大值
}
}
return dp[text1.size()][text2.size()];
}
};
空间优化为一维数组
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector<int>dp(text2.size() + 1,0);
int temp, prev;
for(int i = 1; i < text1.size() + 1; ++i){
prev = dp[0]; // 起始左上角值dp[i-1][j-1]
for(int j = 1; j < text2.size() + 1; ++j){
temp = dp[j];//下一轮左上角的值,防止被修改
if(text1[i - 1] == text2[j - 1]){
dp[j] = prev + 1;
}
else
dp[j]= max(dp[j], dp[j - 1]);
prev = temp;//重要!左上角值移动,作为下一轮左上角的值
}
}
return dp[text2.size()];
}
};
1035.不相交的线(同LCS)
class Solution {
public:
int maxUncrossedLines(vector<int>& A, vector<int>& B) {
vector<int>dp(B.size() + 1, 0);
int pre,temp;
for(int i = 1;i < A.size() + 1; ++i){
pre = dp[0];//本行起始左上角值
for(int j = 1; j < B.size() + 1; ++j){
temp = dp[j];//存下下一轮小轮的左上角值
if(A[i - 1] == B[j - 1])
dp[j] = pre + 1;
else
dp[j] = max(dp[j], dp[j - 1]);
pre = temp;//左上角值移动
}
}
return dp[B.size()];
}
};
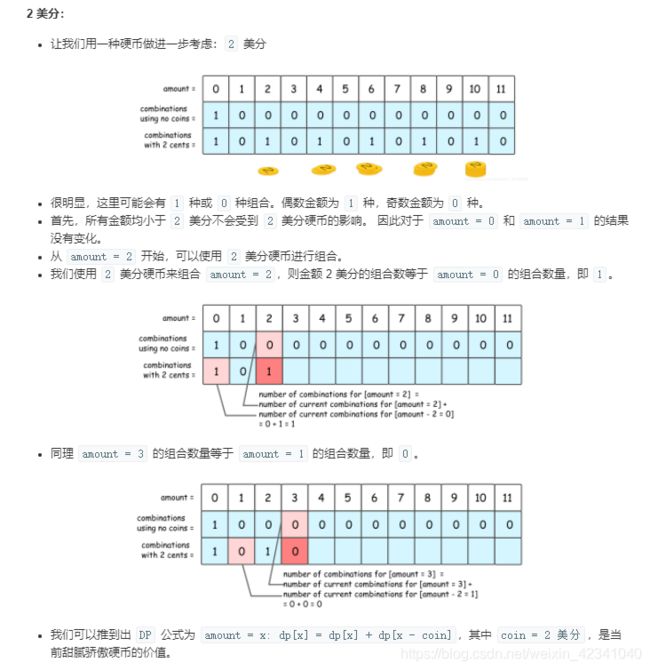
518.零钱兑换二
二维数组
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
vector<vector<int>> dp(n + 1, vector<int>(amount + 1));
//base case:
//amount为0时,方案数为1
for(int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for(int i = 1; i <= amount; i++) {
dp[0][i] = 0;
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= amount; j++) {
if(j - coins[i - 1] >= 0)
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
else dp[i][j] = dp[i - 1][j];
}
}
return dp[n][amount];
}
};
一维数组
复杂度
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int>dp(amount + 1);
dp[0] = 1;//amount为0时,方案数为1
for(auto&coin:coins){
for(int j = 1; j <= amount; ++j){
if(j - coin >= 0)
dp[j] += dp[j - coin];
}
}
return dp[amount];
}
};
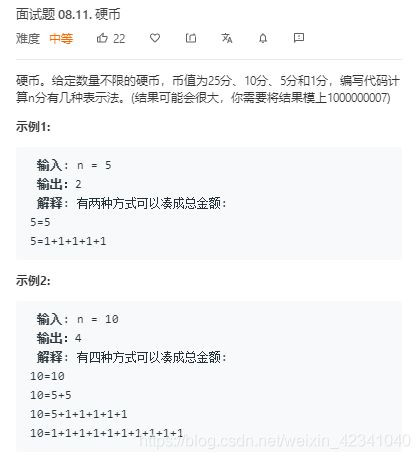
面试题08.11.硬币(同518)
class Solution {
public:
const int N = 1000000007;
int waysToChange(int n) {
vector<int>coins={25,10,5,1};
vector<int>dp(n + 1);
dp[0] = 1;//n为0时,方案数为1
for(auto&coin:coins){
for(int j = 1; j <= n; ++j){
if(j - coin >= 0)
dp[j] += dp[j - coin] % N;
}
}
return dp[n] % N;
}
};
983.最低票价
class Solution {
public:
int mincostTickets(vector<int>& days, vector<int>& costs) {
int lastday = *(days.end() - 1);
vector<int>dp(lastday + 1, INT_MAX);
dp[0] = 0;
int index = 0;
for (int i = 1; i < lastday + 1; ++i) {
if (i == days[index]) {
int _1dayago = i - 1;
int _7daysago = i - 7 > 0 ? i - 7 : 0;//防止越界
int _30daysago = i - 30 > 0 ? i - 30 : 0;
dp[i] = min(dp[i], dp[_1dayago] + costs[0]);
dp[i] = min(dp[i], dp[_7daysago] + costs[1]);
dp[i] = min(dp[i], dp[_30daysago] + costs[2]);
index++;
}
else {
//不在旅行计划的时间不变
dp[i] = dp[i - 1];
}
}
return dp[lastday];
}
};
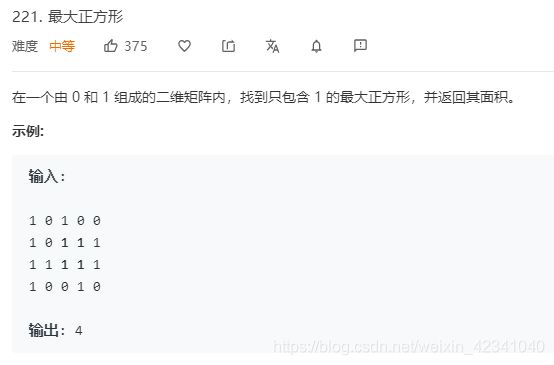
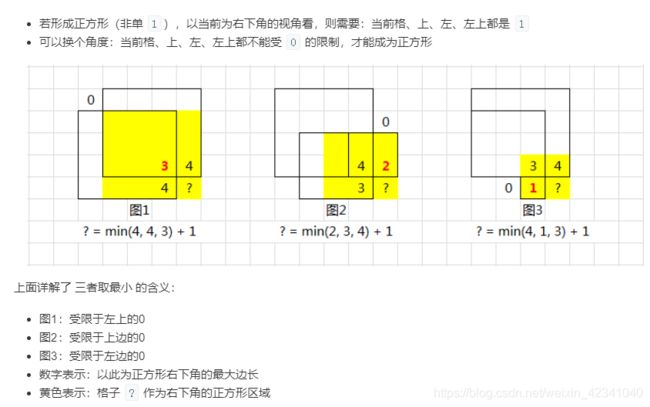
211.最大正方形
为何要取左,上,左上最小值+1(图形解释)
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int row = matrix.size(); //行数
if (!row)
return 0;
int col = matrix[0].size(); //列数
int maxlen = 0;
vector<vector<char>>dp(row, vector<char >(col, '0'));
//初始化第一行
for (int i = 0; i < col; ++i) {
dp[0][i] = matrix[0][i];
maxlen = max(maxlen, dp[0][i] - '0');
}
//初始化第一列
for (int i = 0; i < row; ++i) {
dp[i][0] = matrix[i][0];
maxlen = max(maxlen, dp[i][0] - '0');
}
for (int i = 1; i < row; ++i) {
for (int j = 1; j < col; ++j) {
//如果是0,直接设置为0
if (matrix[i][j] == '0')
dp[i][j] = '0';
else {
//!!左 上 左上最小+1
dp[i][j] = min({ dp[i - 1][j - 1],dp[i - 1][j],dp[i][j - 1] }) + 1;
//统计下
maxlen = max(maxlen, dp[i][j] - '0');
}
}
}
return maxlen * maxlen;
}
};
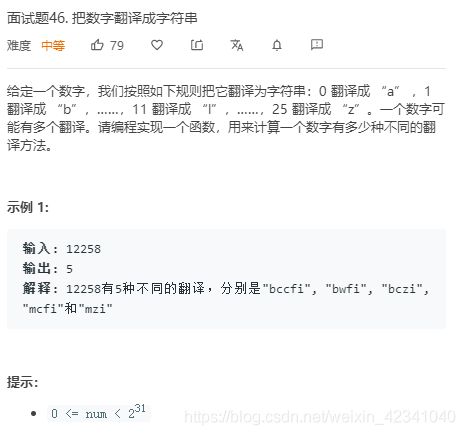
面试题46.把数字翻译成字符串
class Solution {
public:
//dp法 f(i)=f(i-1)+f(i-2) (根据最后一位数字是否和前面的数字拼接)
int translateNum(int num) {
string src = to_string(num);
int p = 0, q = 0, r = 1;//f(-2),f(-1),f(0)
for (int i = 0; i < src.size(); ++i) {
//p变q, q变r, r变q
//q=f(i-1),p=f(i-2)
p = q;
q = r;
r = q;//r = f(i-1)
if (i == 0) {
continue;
}
auto pre = src.substr(i - 1, 2);
//如果要两位数字拼接,只有在这个范围内才是合法的(02,03这些都是不合法)
if (pre <= "25" && pre >= "10") {
r += p; //如果能拼接,再加f(i-2)
}
}
return r;
}
};
复杂度
337.打家劫舍3
关于二叉树的动态规划
思路
class Solution {
public:
/*
每个节点状态,(被选or没有被选),以该节点为根节点的子树的最大利润
*/
struct Node_state {
int selected;
int no_selected;
};
int rob(TreeNode* root) {
auto[select, no_select] = dfs(root);
return max(select, no_select);
}
Node_state dfs(TreeNode* o) {
if (!o)
return { 0,0 };
//后序遍历
auto l = dfs(o->left);
auto r = dfs(o->right);
int select = o->val + l.no_selected + r.no_selected;
int no_select = max(l.selected, l.no_selected ) + max(r.selected ,r.no_selected);
return { select,no_select };
}
};