Python:Numpy的使用
1. Numpy的优势
1.1 Numpy的介绍
Numpy(Numerical Python)是一个开源的Python科学计算库,用于快速处理任意维度的数组。
Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python要简洁的多。
Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
1.2 ndarray介绍
Numpy提供了一个N维数组类型ndarray,它描述了相同类型的“items”的集合。
import numpy as np
score = np.array([[80,89,86,67,79],
[78,97,89,67,81],
[90,94,78,67,74],
[91,91,90,67,69],
[76,87,75,67,86],
[70,79,84,67,84],
[94,92,93,67,64],
[86,85,83,67,80]])
print(score)
[[80 89 86 67 79]
[78 97 89 67 81]
[90 94 78 67 74]
[91 91 90 67 69]
[76 87 75 67 86]
[70 79 84 67 84]
[94 92 93 67 64]
[86 85 83 67 80]]
1.3 ndarray与Python原生list运算效率对比
ndarray计算的速度很快,效率高。
Numpy专门针对ndarray的操作和运算进行了设计,所以数组的存储效率和输入输出性能远优于Python中的嵌套列表,数组越大,Numpy的优势就越明显。
1.4 ndarray的优势
ndarray为什么这么快:
-
存储风格
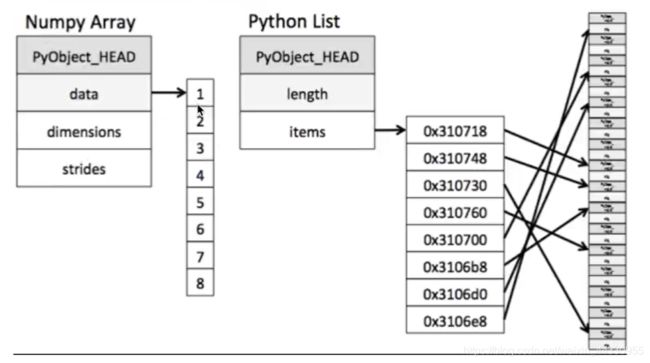
从图中我们可以看出ndarray在存储数据的时候,数据与数据的地址都是连续的,这样就给使得批量操作数组元素时速度更快。
这是因为ndarray中的所有元素的类型都是相同的,而Python列表中的元素类型是任意的,所以ndarray在存储元素时内存可以连续,而python原生lis就t只能通过寻址方式找到下一个元素。
-
并行化运算
Numpy支持并行化运算(向量化运算)。
-
底层语言
Numpy底层使用C语言编写,内部解除了GIL(全局解释器锁),其对数组的操作速度不受Python解释器的限制,效率远高于纯Python代码。
2. 认识n维数组-ndarray属性
2.1 ndarray的属性
其中最重要的是ndarray.shape和ndarray.dtype,下面来具体看看每一种方法:
import numpy as np
score = np.array([[80,89,86,67,79],
[78,97,89,67,81],
[90,94,78,67,74],
[91,91,90,67,69],
[76,87,75,67,86],
[70,79,84,67,84],
[94,92,93,67,64],
[86,85,83,67,80]])
# 数组的形状,使用一个元组表示:(行数, 列数)
a = score.shape
print('数组的形状:' + str(a))
# 数组的维度
b = score.ndim
print('数组的维度:' + str(b))
# 数组的元素个数
c = score.size
print('数组的元素个数:' + str(c))
# 数组的类型
d = score.dtype
print('数组的类型:' + str(d))
# 数组一个元素字节长度
e = score.itemsize
print('数组一个元素字节长度:' + str(e))
数组的形状:(8, 5)
数组的维度:2
数组的元素个数:40
数组的类型:int32
数组一个元素字节长度:4
2.2 ndarray的形状
ndarray的形状有一维数组、二维数组、三维数组…
根据嵌套情况来判断,或者使用.shape,元组中有几个数就是几维
2.3 ndarray的类型
创建adarray时可以指定数据类型
import numpy as np
score = np.array([[80,89,86,67,79],
[78,97,89,67,81],
[90,94,78,67,74],
[91,91,90,67,69],
[76,87,75,67,86],
[70,79,84,67,84],
[94,92,93,67,64],
[86,85,83,67,80]],
dtype = 'float32')
# 数组的类型
d = score.dtype
print('数组的类型:' + str(d))
# 数组一个元素字节长度
e = score.itemsize
print('数组一个元素字节长度:' + str(e))
数组的类型:float32
数组一个元素字节长度:4
3. 基本操作
3.1 生成数组的方法
-
生成0和1的数组
np.zeros()、np.ones()下面来具体看看:
import numpy as np # 括号内是列表 a1 = np.zeros([2, 3]) # 括号内是元组 b1 = np.zeros((2, 3)) # 设置数组类型方法一 c1 = np.zeros(shape = [2, 3], dtype = 'int32') # 设置数组类型方法二 d1 = np.zeros(shape = [2, 3], dtype = np.int32) # 括号内是列表 a2 = np.ones([2, 3]) # 括号内是元组 b2 = np.ones((2, 3)) # 设置数组类型方法一 c2 = np.ones(shape = [2, 3], dtype = 'int32') # 设置数组类型方法二 d2 = np.ones(shape = [2, 3], dtype = np.int32) -
从现有数组中生成
有np.array()、方法np.asarray()、np.copy()有三种方法,下面来比较下:
import numpy as np score = np.array([[80,89,86,67,79], [78,97,89,67,81], [90,94,78,67,74], [91,91,90,67,69], [76,87,75,67,86], [70,79,84,67,84], [94,92,93,67,64], [86,85,83,67,80]]) # 使用方法np.array() data1 = np.array(score) print('修改前array:' + str(data1)) # 使用方法np.asarray() data2 = np.asarray(score) print('修改前asarray:' + str(data2)) # 使用方法np.copy() data3 = np.copy(score) print('修改前copy:' + str(data3)) score[2, 1] = 1000 print('修改后array:' + str(data1)) print('修改后asarray:' + str(data2)) print('修改后copy:' + str(data3))修改前array:[[80 89 86 67 79] [78 97 89 67 81] [90 94 78 67 74] [91 91 90 67 69] [76 87 75 67 86] [70 79 84 67 84] [94 92 93 67 64] [86 85 83 67 80]] 修改前asarray:[[80 89 86 67 79] [78 97 89 67 81] [90 94 78 67 74] [91 91 90 67 69] [76 87 75 67 86] [70 79 84 67 84] [94 92 93 67 64] [86 85 83 67 80]] 修改前copy:[[80 89 86 67 79] [78 97 89 67 81] [90 94 78 67 74] [91 91 90 67 69] [76 87 75 67 86] [70 79 84 67 84] [94 92 93 67 64] [86 85 83 67 80]] 修改后array:[[80 89 86 67 79] [78 97 89 67 81] [90 94 78 67 74] [91 91 90 67 69] [76 87 75 67 86] [70 79 84 67 84] [94 92 93 67 64] [86 85 83 67 80]] 修改后asarray:[[ 80 89 86 67 79] [ 78 97 89 67 81] [ 90 1000 78 67 74] [ 91 91 90 67 69] [ 76 87 75 67 86] [ 70 79 84 67 84] [ 94 92 93 67 64] [ 86 85 83 67 80]] 修改后copy:[[80 89 86 67 79] [78 97 89 67 81] [90 94 78 67 74] [91 91 90 67 69] [76 87 75 67 86] [70 79 84 67 84] [94 92 93 67 64] [86 85 83 67 80]]说明asarray是深拷贝,array和copy是浅拷贝。
-
生成固定范围的数组
有np.linspace(a,b,c)、np.arange(a,b,c)两种方法,下面来具体看看:
import numpy as np # np.linspace(a,b,c) # 代表从[a,b]等距离生成c个数 data1 = np.linspace(0, 100, 9) print(data1) # np.arange(a,b,c) # 代表从[a,b)生成的数与数的距离为c data2 = np.arange(0, 10, 2) print(data2)[ 0. 12.5 25. 37.5 50. 62.5 75. 87.5 100. ] [0 2 4 6 8] -
生成随机数组
-
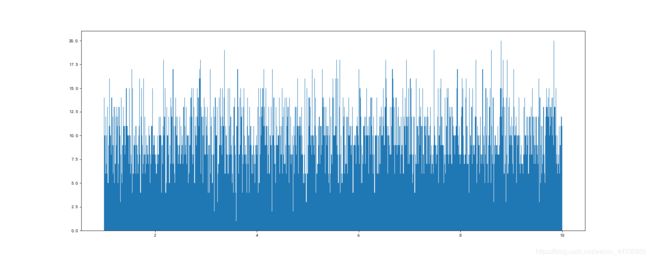
生成均匀分布数组
import numpy as np import matplotlib.pyplot as plt # 1.准备数据 # 代表均匀生成10000个从1到10之间的数 data1 = np.random.uniform(1, 10, 10000) # 2.创建画布 plt.figure(figsize = (20, 8), dpi = 80) # 3.绘制图像 # data代表要统计的数据 # 1000代表将将要统计的数据分为5组 plt.hist(data1, 1000) # 4.显示图像 plt.show() -
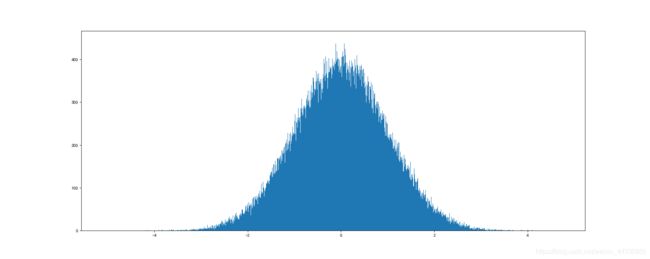
生成正态分布数组
import numpy as np import matplotlib.pyplot as plt # 1.准备数据 # 代表生成均值为0,方差为1,有1000000个这样数据的列表 data1 = np.random.normal(0, 1, 1000000) # 2.创建画布 plt.figure(figsize = (20, 8), dpi = 80) # 3.绘制图像 # data代表要统计的数据 # 10000代表将将要统计的数据分为10000组 plt.hist(data1, 10000) # 4.显示图像 plt.show()
-
3.2 数组的索引、切片
数组进行索引和切片操作i:
-
一维数组
import numpy as np # 创建一个一维数组 a = np.array([1, 2, 3, 4, 5, 6]) # 进行索引操作 print(a[0]) # 进行切片操作 # 左闭右开 print(a[0:5])1 [1 2 3 4 5] -
二维数组
import numpy as np # 创建一个二维数组 b = np.array([[80,89,86,67,79], [78,100,89,67,81], [90,94,78,67,74], [94,92,93,67,64], [86,85,83,67,80]]) # 进行索引操作 print(b[1, 1]) # 进行切片操作 # '1'代表第二行,'0:3'代表第二行的前三个数 print(b[1, 0:3])100 [ 78 100 89] -
三维数组
import numpy as np # 创建一个三维数组 c = np.array([[[80,89,86,67,79], [78,100,89,67,81], [90,94,78,67,74], [94,92,93,67,64], [86,85,83,67,80]]]) # 进行索引操作 print(c[0,1,1]) # 进行切片操作 print(c[0, 1, 0:3])100 [ 78 100 89]
3.3 形状修改
有三种方法进行形状的修改:
- 方法一:newndarray = ndarray.reshape()
- 方法二:ndarry.resize()
- 方法三:ndarry.T
下面来进行比较:
import numpy as np
# 创建一个二维数组
a = np.array([[80,89,86,67,79],
[78,100,89,67,81],
[86,85,83,67,80]])
# 使用方法newndarray = ndarray.reshape()
# 有返回值,不对原有数据进行转置
new_a = a.reshape(5, 3)
print('使用reshape():' +'\n' + str(new_a))
# 使用方法ndarry.resize()
# 无返回值,对原有数据进行转置
a.resize(5,3)
print('使用resize():' +'\n' + str(a))
# 使用方法ndarry.T
# 无返回值,不对原有数据进行转置,只有在使用.T时才转置
print('使用T:' +'\n' + str(a.T))
使用reshape():
[[ 80 89 86]
[ 67 79 78]
[100 89 67]
[ 81 86 85]
[ 83 67 80]]
使用resize():
[[ 80 89 86]
[ 67 79 78]
[100 89 67]
[ 81 86 85]
[ 83 67 80]]
使用T:
[[ 80 67 100 81 83]
[ 89 79 89 86 67]
[ 86 78 67 85 80]]
3.4 类型修改
有两种方法进行类型的修改:
- 使用ndarray.astype()进行类型的修改。
- 使用ndarray.tostring()进行序列化,保存到本地。
下面来具体比较下:
import numpy as np
# 创建一个二维数组
a = np.array([[80,89,86,67,79],
[78,100,89,67,81],
[86,85,83,67,80]])
# 使用ndarray.astype()进行类型的修改
# 可以有返回值类型,不对原始数据进行修改
print(a.astype('float32'))
# 使用ndarray.tostring()进行序列化,保存到本地
print(a.tostring())
[[ 80. 89. 86. 67. 79.]
[ 78. 100. 89. 67. 81.]
[ 86. 85. 83. 67. 80.]]
b'P\x00\x00\x00Y\x00\x00\x00V\x00\x00\x00C\x00\x00\x00O\x00\x00\x00N\x00\x00\x00d\x00\x00\x00Y\x00\x00\x00C\x00\x00\x00Q\x00\x00\x00V\x00\x00\x00U\x00\x00\x00S\x00\x00\x00C\x00\x00\x00P\x00\x00\x00'
3.5 数组的去重
使用np.unique()方法进行数组的去重
import numpy as np
# 创建一个二维数组
a = np.array([[80,89,86,67,79],
[78,100,89,67,81],
[86,85,83,67,80]])
# 使用np.unique()方法进行数组的去重
# 有返回值,不对原有数据进行修改
print(np.unique(a))
[ 67 78 79 80 81 83 85 86 89 100]
4. ndarray运算
4.1 逻辑运算
主要是np.all()、np.any()、np.wherer()三个方法的使用
import numpy as np
# 生成一个8行10列的标准正态分布的二维数组
# 代表8支股票10天的涨幅情况
data = np.random.normal(loc =0, scale = 1, size = (8,10))
print('原始数据' + '\n' + str(data))
# 需求1:8支股票10天如果涨跌幅大于0.5就标记为True,否则为False
print('需求1' + '\n' + str(data > 0.5))
# 需求2:前3支股票前5天如果涨跌幅大于0.5就标记为True,否则为False
print('需求2' + '\n' + str(data[0:3, 0:5] > 0.5))
# 需求3:股票如果涨跌幅大于0.5,则标记为1,否则为0
# data[]中传递的是布尔值,不能是其他数据
data[data > 0.5] = 1
print('需求3' + '\n' + str(data))
原始数据
[[ 0.83886781 0.6069855 0.80865936 -1.16895959 -2.09760814 0.62323489
-0.34492482 -1.60124892 -0.55024986 -0.95986343]
[-1.54374376 0.52759955 0.87870201 2.67280895 1.067674 -1.15614495
0.50872886 2.51069133 -0.99770796 -0.02567882]
[ 1.09679682 -0.41084766 0.50589611 -0.92443376 -0.84711761 0.4000614
1.2457309 -0.68819461 -0.64765538 -0.24950491]
[ 0.13768991 0.33223589 0.19751889 -0.85598566 0.03029228 0.30495726
1.1824456 0.82183664 1.89418781 -0.10182856]
[-2.15338839 1.99478745 0.46251004 -0.23795407 0.19862356 -0.68163819
-0.19186438 1.27409356 0.301477 -0.43326793]
[-1.56409593 -0.06941236 -2.47672878 -0.59172057 -1.03028201 -0.21272101
2.88081077 0.53148962 -0.33871506 0.68933348]
[-2.3376821 -1.27299444 -0.16487271 1.36572759 1.24535189 0.20982072
0.93941999 1.11054398 -2.19532362 0.5933207 ]
[ 1.0011553 -1.35618182 0.96510902 -0.76907634 0.10349159 0.228885
-1.65697367 -1.82298863 -0.11080476 0.38423467]]
需求1
[[ True True True False False True False False False False]
[False True True True True False True True False False]
[ True False True False False False True False False False]
[False False False False False False True True True False]
[False True False False False False False True False False]
[False False False False False False True True False True]
[False False False True True False True True False True]
[ True False True False False False False False False False]]
需求2
[[ True True True False False]
[False True True True True]
[ True False True False False]]
需求3
[[ 1. 1. 1. -1.16895959 -2.09760814 1.
-0.34492482 -1.60124892 -0.55024986 -0.95986343]
[-1.54374376 1. 1. 1. 1. -1.15614495
1. 1. -0.99770796 -0.02567882]
[ 1. -0.41084766 1. -0.92443376 -0.84711761 0.4000614
1. -0.68819461 -0.64765538 -0.24950491]
[ 0.13768991 0.33223589 0.19751889 -0.85598566 0.03029228 0.30495726
1. 1. 1. -0.10182856]
[-2.15338839 1. 0.46251004 -0.23795407 0.19862356 -0.68163819
-0.19186438 1. 0.301477 -0.43326793]
[-1.56409593 -0.06941236 -2.47672878 -0.59172057 -1.03028201 -0.21272101
1. 1. -0.33871506 1. ]
[-2.3376821 -1.27299444 -0.16487271 1. 1. 0.20982072
1. 1. -2.19532362 1. ]
[ 1. -1.35618182 1. -0.76907634 0.10349159 0.228885
-1.65697367 -1.82298863 -0.11080476 0.38423467]]
import numpy as np
# 生成一个8行10列的标准正态分布的二维数组
# 代表8支股票10天的涨幅情况
data = np.random.normal(loc =0, scale = 1, size = (8,10))
# 需求4:判断data[0:3, 0:4]的股票是否全部大于0
# 使用函数np.all()
# 必须全部数据符合条件才返回True,否则为False
temp1 = data[0:3, 0:4]
print('需求4' + '\n' + str(np.all(temp1)))
# 需求5:判断data[0:3, 0:4]的股票是否有大于0的
# 使用函数np.any()
# 有一个数据符合条件就返回True,全部不符合则为False
temp2 = data[0:3, 0:4]
print('需求5' + '\n' + str(np.all(temp2)))
需求4
True
需求5
True
import numpy as np
# 生成一个8行10列的标准正态分布的二维数组
# 代表8支股票10天的涨幅情况
data = np.random.normal(loc =0, scale = 1, size = (8,10))
# 需求6:判断前四个股票前四天的涨跌幅大于0的置为1,否则为0
# 使用函数np.where()
temp = data[0:4, 0:4]
# where()中传递三个参数
# 第一个为判读条件
# 第二个为符合条件所进行的操作
# 第三个为不符合条件进行的操作
print('需求6' + '\n' + str(np.where(temp > 0, 1, 0)))
# 复合逻辑需结合np.logical_and和np.logical_or使用
# 需求7:判断前四个股票前四天的涨跌幅,大于0.5并且小于1的置为1,否则为0
print('需求7' + '\n' + str(np.where(np.logical_and(temp>0.5,temp<1),1,0)))
# 需求8:判断前四个股票前四天的涨跌幅,大于0.5并且小于-0.5的置为1,否则为0
print('需求8' + '\n' + str(np.where(np.logical_or(temp>0.5,temp<-0.5),1,0)))
需求6
[[0 0 0 0]
[1 0 1 0]
[0 0 1 0]
[0 1 0 1]]
需求7
[[0 0 0 0]
[0 0 1 0]
[0 0 0 0]
[0 0 0 1]]
需求8
[[1 0 0 1]
[1 0 1 0]
[0 0 1 0]
[0 0 0 1]]
4.2 统计运算
import numpy as np
# 创建一个5行5列的标准正态分布的二维数组
# 代表5支股票5天的涨幅情况
data = np.array([[80,89,86,67,79],
[78,100,89,67,81],
[90,94,78,67,74],
[94,92,93,67,64],
[86,85,83,67,80]])
# 需求1:统计每支股票10天内的最大值
# 第一个参数为数据,第二个参数表示按照行还是列进行计算,1为行,2为列
print('最大值' + str(np.max(data, axis = 1)))
# 需求2:统计每支股票5天内的最小值
print('最小值' + str(np.min(data, axis = 1)))
# 需求3:统计每支股票5天内的平均值
print('平均值' + str(np.mean(data, axis = 1)))
# 需求4:统计每支股票5天内的中位数
print('中位数' + str(np.median(data, axis = 1)))
# 需求5:统计每支股票5天内的方差
print('方差' + str(np.var(data, axis = 1)))
# 需求6:统计每支股票5天内的标注差
print('标准差' + str(np.std(data, axis = 1)))
# 需求7:统计每支股票5天内的最大值所在的下标
print('最大值' + str(np.argmax(data, axis = 1)))
# 需求8:统计每支股票5天内的最小值所在的下标
print('最大值' + str(np.argmin(data, axis = 1)))
最大值[ 89 100 94 94 86]
最小值[67 67 67 64 67]
平均值[80.2 83. 80.6 82. 80.2]
中位数[80. 81. 78. 92. 83.]
方差[ 57.36 122. 100.64 182.8 47.76]
标准差[ 7.57363849 11.04536102 10.03194896 13.52035502 6.91086102]
最大值[1 1 1 0 0]
最大值[3 3 3 4 3]
4.3 数组间运算
import numpy as np
data = np.array([[1,2,3,4,5],
[6,7,8,9,10]])
# 使用np创建的数组可直接对其进行加减乘除
print('使用加法:' + '\n' + str(data + 1))
print('使用减法:' + '\n' + str(data - 2))
print('使用乘法:' + '\n' + str(data * 3))
print('使用除法:' + '\n' + str(data / 4))
使用加法:
[[ 2 3 4 5 6]
[ 7 8 9 10 11]]
使用减法:
[[-1 0 1 2 3]
[ 4 5 6 7 8]]
使用乘法:
[[ 3 6 9 12 15]
[18 21 24 27 30]]
使用除法:
[[0.25 0.5 0.75 1. 1.25]
[1.5 1.75 2. 2.25 2.5 ]]
数组与数组间的运算需要进行条件判断,必须满足以下其中一个条件:
- 总维度相同
- 同一维度下有1出现
如果可以进行运算,则运算后的维度为每个维度对应的最大值。
下面是可以进行运算的例子:
下面是不可以进行运算的例子:
4.4 矩阵间的运算
矩阵必须是二维的。
矩阵一定是二维数组,二维数组不一定是矩阵。
矩阵间的乘法必须满足:(m, n)*(n, l)= (m, l),即第一个矩阵的列数与第二个矩阵的行数相等。
import numpy as np
# 数据
data = np.array([[1,2],
[6,7],
[3,6],
[1,1],
[7,8]])
# 权重
weight = np.array([[1,2],
[5,6]])
# 使用np.array()创建的矩阵可使用两种方法进行矩阵的乘法
# 方法一:np.matmul
print('方法一:' + '\n' + str(np.matmul(data,weight)))
# 方法二:np.dot
print('方法二:' + '\n' + str(np.dot(data,weight)))
方法一:
[[11 14]
[41 54]
[33 42]
[ 6 8]
[47 62]]
方法二:
[[11 14]
[41 54]
[33 42]
[ 6 8]
[47 62]]
5. 合并、分割
5.1 合并
import numpy as np
a = np.array([1,2,3])
b = np.array([2,3,4])
c = np.array([[1],
[2],
[3]])
d = np.array([[2],
[3],
[4]])
# 进行水平合并
print('水平合并:')
print(np.hstack((a, b)))
print(np.hstack((c, d)))
# 进行竖直合并
print('竖直合并:')
print(np.vstack((a, b)))
print(np.vstack((c, d)))
水平合并:
[1 2 3 2 3 4]
[[1 2]
[2 3]
[3 4]]
竖直合并:
[[1 2 3]
[2 3 4]]
[[1]
[2]
[3]
[2]
[3]
[4]]
import numpy as np
a = np.array([[1,2],
[3,4]])
b = np.array([[5,6]])
# 进行水平合并
print('水平合并:')
# 需要传递两个参数,一个为数据,一个为轴
print(np.concatenate((a, b.T), axis = 1))
print('竖直合并:')
print(np.concatenate((a, b), axis = 0))
水平合并:
[[1 2 5]
[3 4 6]]
竖直合并:
[[1 2]
[3 4]
[5 6]]
##5.2 分割
分割并不常用