4 泰坦尼克号问题

背景：泰坦尼克号估计都耳熟能详了，讲的故事是一个游艇倒了，大家都急忙逃生，但是救生艇的数量是有限的，没法分配一人一个，船长此时说：lady and kid first！我们设计的模型的目的是根据游客的这些个人信息及其存活状况，建立合适的模型，并预测其他人的存活状况。（这是kaggle中的一个案例）

4.1数据探索

数据的获取可以从kaggle官网上下载，首先我们先看看数据的情况，初步探索。

# encoding=utf-8
import pandas as pd
import numpy as np
from pandas import Series,DataFrame

data_train=pd.read_csv("train.csv")
pd.set_option("display.width",300)
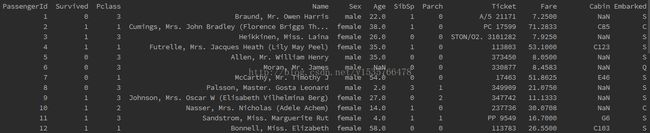
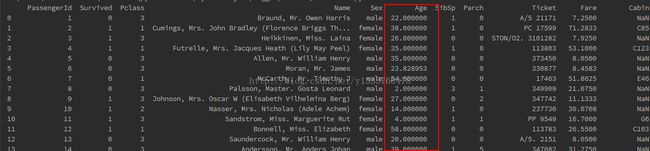
print data_train

 

• PassengerId => 乘客ID
• Pclass => 乘客等级(1/2/3等舱位)
• Name => 乘客姓名
• Sex => 性别
• Age => 年龄
• SibSp => 堂兄弟/妹个数
• Parch => 父母与小孩个数
• Ticket => 船票信息
• Fare => 票价
• Cabin => 客舱
• Embarked => 登船港口

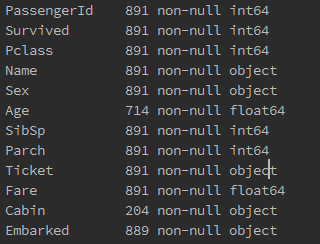
data_train.info()

从上图中我们能获取的信息是Age和Cabin以及Embarked中存在缺失值，Cabin缺失值较多。

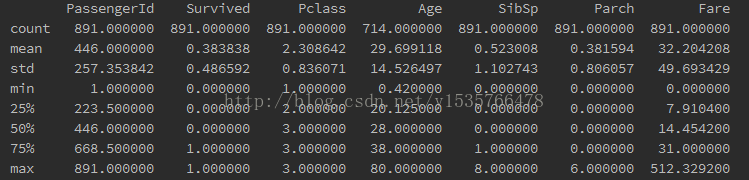
print data_train.describe()

初步看到的信息是：只有0.383838的人最终获救了，以及获救的人在1舱比较少，多数集中在2,3舱。

4.2 对数据的初步分析

根据以上的信息，我们仍毫无头绪，每个属性与Survived之间的关系又是怎样的呢？即将揭晓……

4.2.1乘客各属性分布

数和图，一般我们倾向于看图，那么我就对数据进行可视化处理。将乘客的每个属性可视化。

import matplotlib.pyplotas plt
import matplotlib as mpl
fig=plt.figure()
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
fig.set(alpha=0.3)
plt.subplot2grid((2,3),(0,0))
data_train.Survived.value_counts().plot(kind='bar')
plt.title(u"获救情况（1为得救）")
plt.ylabel(u'人数')
plt.subplot2grid((2,3),(0,1))
data_train.Pclass.value_counts().plot(kind='bar')
plt.ylabel(u"人数")
plt.title(u"乘客等级分布")
plt.subplot2grid((2,3),(0,2))
plt.scatter(data_train.Survived,data_train.Age)
plt.ylabel(u"年龄")
plt.grid(b=True,which='major',axis='y')
plt.title(u"按年龄看获救分布(1为获救)")
plt.subplot2grid((2,3),(1,0),colspan=2)
data_train.Age[data_train.Pclass==1].plot(kind='kde')
data_train.Age[data_train.Pclass==2].plot(kind='kde')
data_train.Age[data_train.Pclass==3].plot(kind='kde')
plt.xlabel(u'年龄')
plt.ylabel(u'密度')
plt.title(u'各等级的乘客年龄分布')
plt.legend((u'头等舱',u'2等舱',u'3等舱'),loc='best')
plt.subplot2grid((2,3),(1,2))
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u'各登船口岸上船人数')
plt.ylabel(u'人数')
plt.show()

 

    从上图我们可以看出，幸存的人不到一般，300左右；3等舱的人数比较多；头等舱中40岁左右的人比较多，而2,3等舱20多岁的人比较多；登船港口人数按照S、C、Q递减，并且S港口的人非常多，比其他两个的加和还多。此时在想是不是不同舱位的乘客等级与财富有关相应的与幸存率也有关？年龄是否对幸存有关？（这个应该是肯定的，毕竟前面提到小孩和女士先走……）这么一来性别和幸存应该也有关，那和登船港口是否有关？这些疑问需要做进一步统计才能得知。

4.2.2 属性与幸存关联统计

话不多说，直接上代码:

（1）

#各乘客等级的幸存情况
fig.set(alpha=0.3)
Survived_0=data_train.Pclass[data_train.Survived==0].value_counts()
Survived_1=data_train.Pclass[data_train.Survived==1].value_counts()
df=pd.DataFrame({u'获救':Survived_1,u"未获救":Survived_0})
df.plot(kind='bar',stacked=True)
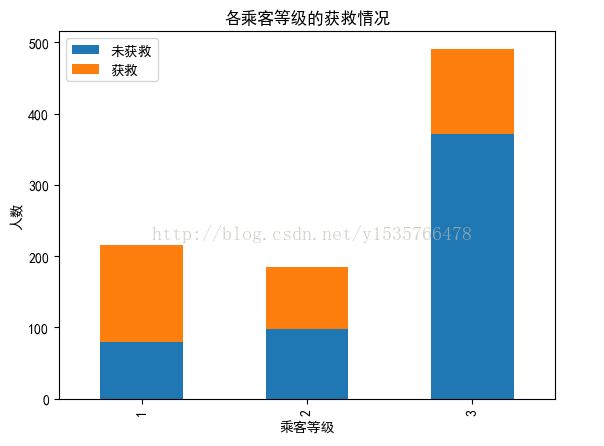
plt.title(u'各乘客等级的获救情况')
plt.xlabel(u'乘客等级')
plt.ylabel(u'人数')
plt.show()

显然头等舱获救的几率更大些，因此乘客等级应作为特征加入后面的模型中。

（2）

#性别对获救的影响
fig.set(alpha=0.3)
Survived_m=data_train.Survived[data_train.Sex=='male'].value_counts()
Survived_f=data_train.Survived[data_train.Sex=='female'].value_counts()
df=pd.DataFrame({u'男性':Survived_m,u'女性':Survived_f})
df.plot(kind='bar',stacked=True)
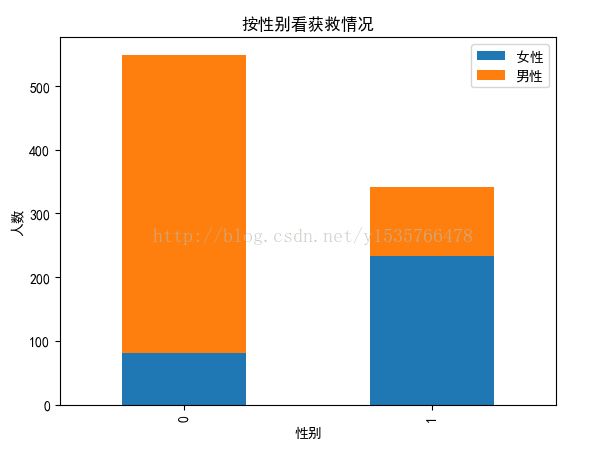
plt.title(u'按性别看获救情况')
plt.xlabel(u'性别')
plt.ylabel(u'人数')
plt.show()

 

这张图明显可以看出女性获救几率远大与男性，和之前提到的妇女先走一致。因此性别要作为重要的特征加入到模型当中。

（3）

#各种舱级别情况下各性别的获救情况
fig.set(alpha=0.4)#设置图形的透明度
plt.ylim(0,300)
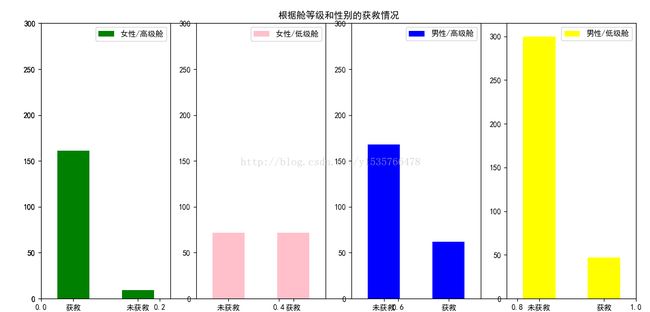
plt.title(u"根据舱等级和性别的获救情况")
ax1=fig.add_subplot(141)
data_train.Survived[data_train.Sex=='female'][data_train.Pclass!=3].value_counts().plot(kind='bar',label='female highclass',color='green')
ax1.set_xticklabels([u"获救",u'未获救'],rotation=0)
ax1.legend([u"女性/高级舱"],loc='best')

fig.set(alpha=0.4)#设置图形的透明度
plt.ylim(0,300)
ax1=fig.add_subplot(142)
data_train.Survived[data_train.Sex=='female'][data_train.Pclass==3].value_counts().plot(kind='bar',label='female highclass',color='pink')
ax1.set_xticklabels([u"未获救",u'获救'],rotation=0)
ax1.legend([u"女性/低级舱"],loc='best')

fig.set(alpha=0.4)#设置图形的透明度
plt.ylim(0,300)
ax1=fig.add_subplot(143)
data_train.Survived[data_train.Sex=='male'][data_train.Pclass!=3].value_counts().plot(kind='bar',label='female highclass',color='blue')
ax1.set_xticklabels([u"未获救",u'获救'],rotation=0)
ax1.legend([u"男性/高级舱"],loc='best')

fig.set(alpha=0.4)#设置图形的透明度
plt.ylim(0,300)
ax1=fig.add_subplot(144)
data_train.Survived[data_train.Sex=='male'][data_train.Pclass==3].value_counts().plot(kind='bar',label='female highclass',color='yellow')
ax1.set_xticklabels([u"未获救",u'获救'],rotation=0)
ax1.legend([u"男性/低级舱"],loc='best')
plt.show()

 

从图可以明显的看出位于高等舱的女性获救几率非常大；位于低等舱的女性获救率为1/2左右；位于低等舱的男性获救率更小了，这证实了之前的判断（女性获救几率大，高等舱的获救几率大）

（4）

#港口的不同与获救的关系

fig.set(alpha=0.5)
Survived_0=data_train.Embarked[data_train.Survived==0].value_counts()
Survived_1=data_train.Embarked[data_train.Survived==1].value_counts()
df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)
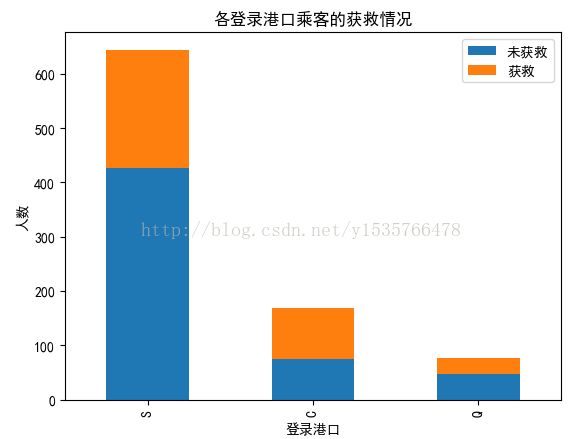
plt.title(u"各登录港口乘客的获救情况")
plt.xlabel(u"登录港口")
plt.ylabel(u"人数")
plt.show()

 

从图中不可以看出太明显的关系，作为备选特征

（5）

#堂兄弟/妹，孩子/父母的人数，对获救情况的影响
g=data_train.groupby(['SibSp','Survived'])
df=pd.DataFrame(g.count()['PassengerId'])
print df

g=data_train.groupby(['Parch','Survived'])
df=pd.DataFrame(g.count()['PassengerId'])
print df

 

也没有看出很明显的关系，作为备选特征。

（1）  

上文也提到Cabin缺失值非常多，一般处理缺失值的方法有：当总数据非常大的时候可以直接把缺失值删除，当总数据量小的时候可以将缺失值补全。现在先将Cabin按缺失与否作为条件，我们在这个角度看一下它和Survived的关系。

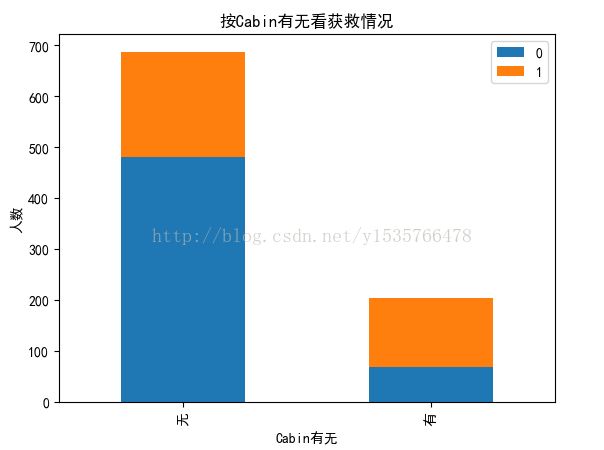
#Cabin的缺失与否与Survived的关系
fig.set(alpha=0.6)
Survived_cabin=data_train.Survived[pd.notnull(data_train.Cabin)].value_counts()
Survived_nocabin=data_train.Survived[pd.isnull(data_train.Cabin)].value_counts()
df=pd.DataFrame({u'有':Survived_cabin, u'无':Survived_nocabin}).transpose()
df.plot(kind='bar', stacked=True)
plt.title(u"按Cabin有无看获救情况")
plt.xlabel(u"Cabin有无")
plt.ylabel(u"人数")
plt.show()

 

似乎有点出乎意料，居然Cabin存在的时候获救几率很大，可以作为备选特征。

4.3简单的数据预处理

上一节我们对数据的大体情况有了一个了解，这一节我们该对数据进行处理了，为建模做准备。

我们用随机森林拟合缺失的年龄数据，随机森林可以降低过拟合的现象。

#拟合数据
from sklearn.ensemble import RandomForestRegressor
#使用 随机森林补缺失的年龄属性
def set_missing_ages(df):
    # 把已有的数值型特征取出来丢进Random Forest Regressor中
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
    # 乘客分成已知年龄和未知年龄两部分
    known_age = age_df[age_df.Age.notnull()].as_matrix()
    unknown_age = age_df[age_df.Age.isnull()].as_matrix()
    # y即目标年龄
    y = known_age[:, 0]
    # X即特征属性值
    X = known_age[:, 1:]
    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    rfr.fit(X, y)
    # 用得到的模型进行未知年龄结果预测
    predictedAges = rfr.predict(unknown_age[:, 1::])
    # 用得到的预测结果填补原缺失数据
    df.loc[(df.Age.isnull()), 'Age' ] = predictedAges
    print df, rfr
    return df, rfr
def set_Cabin_type(df):
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    print df
    return df
data_train, rfr = set_missing_ages(data_train)
data_train = set_Cabin_type(data_train)

这样我们的目的达到了。但是在建模时输入的特征都是数值型的特征，因此我们首先要对类目型的特征因子化

#特征因子化
dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')
df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
print df

 

我们再观察数据的时候发现Age和Fare两个属性，乘客数值幅度变化太大，我们要对其进行标准化处理，否则将对收敛造成很严重的影响。

#标准化处理
import sklearn.preprocessing as preprocessing
scaler = preprocessing.StandardScaler()
age_scale_param = scaler.fit(df['Age'])
df['Age_scaled'] = scaler.fit_transform(df['Age'], age_scale_param)
fare_scale_param = scaler.fit(df['Fare'])
df['Fare_scaled'] = scaler.fit_transform(df['Fare'], fare_scale_param)
print df

这两列数据在【-1,1】之间，现在数据已经准备好了，就等建模了。……不对，忘了件大事，测试数据也得进行处理，那么开始吧~~

#测试数据的处理
data_test = pd.read_csv("test.csv")
data_test.loc[ (data_test.Fare.isnull()), 'Fare' ] = 0
# 接着我们对test_data做和train_data中一致的特征变换
# 首先用同样的RandomForestRegressor模型填上丢失的年龄
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].as_matrix()
# 根据特征属性X预测年龄并补上
X = null_age[:, 1:]
predictedAges = rfr.predict(X)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')
df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df_test['Age_scaled'] = scaler.fit_transform(df_test['Age'], age_scale_param)
df_test['Fare_scaled'] = scaler.fit_transform(df_test['Fare'], fare_scale_param)
print df_test

这样万事具备只欠东风了。

4.4 逻辑回归建模

本案例用逻辑回归对其进行建模

from sklearn import linear_model

# 用正则取出我们要的属性值
train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
train_np = train_df.as_matrix()

# y即Survival结果
y = train_np[:, 0]
# X即特征属性值
X = train_np[:, 1:]
# fit到RandomForestRegressor之中
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
clf.fit(X, y)

模型如下

最后一步进行预测：

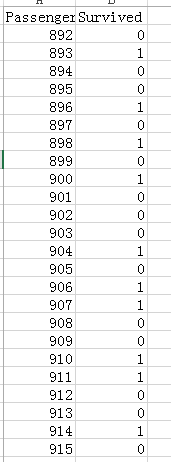
#进行预测
test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions = clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].as_matrix(), 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_predictions.csv", index=False)

结果如下：

当我们把结果提交时发现准确率是0.76555，虽然准确率并不高但是是我们初步探索形成的模型，也还可以啦。

4.4 逻辑回归系统优化

我们首先将模型系数与特征关联起来

#模型系数与特征关联
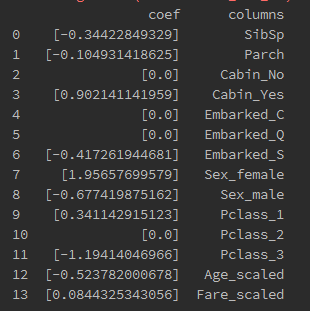
print pd.DataFrame({"columns":list(train_df.columns)[1:],"coef":list(clf.coef_.T)})

图中+表示该特征和结果是正相关，-表示该特征和结果是负相关。观察发现：

（1） SibSp和Parch和解果是负相关的

（2） Cabin值的存在会很大程度上会很大程度上提高获救率

（3） Embarked属性，Embarked_S值在一定程度上会降低其获救率，这是我们在之前的统计中没有发现的规律

（4） Sex属性，女性与获救率存在强烈的正相关，而男性则是负相关的

（5） Pclass属性头等舱的人更容易获救，而三等舱的人与获救率是负相关的

（6） Age属性，年龄越小越容易获救，与“小孩先走”一致

（7） Fare属性，在很小程度上是正相关的。

4.5 交叉验证

我们进行交叉验证，将训练集的数据分为两部分，一部分用于训练模型，一部分用于在查看模型的效果。

4.5.1 数据分割生成模型

#数据分割
from sklearn import cross_validation
split_train,split_cv=cross_validation.train_test_split(df,test_size=0.3,random_state=0)
train_df=split_train.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
#filter()根据判断结果自动过滤掉不符合条件的元素，返回由符合条件元素组成的新list
#生成模型
clf2=linear_model.LogisticRegression(C=1.0,penalty='l1',tol=1e-6)#C正则化的程度，越小则更强的正则化，tol绝对误差限
clf2.fit(train_df.as_matrix()[:,1:],train_df.as_matrix()[:,0])
#对cross validation数据进行预测
cv_df=split_cv.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions=clf2.predict(cv_df.as_matrix()[:,1:])
origin_data_train=pd.read_csv("train.csv")
from sklearn import metrics
print metrics.accuracy_score(predictions, cv_df.as_matrix()[:,0])

 

模型的正确率提高了~~~，说明交叉验证很有效。

4.6 模型的融合

模型融合可以很好的缓解过拟合的问题，对精确度的提升有一定的帮助。在训练的时候我们不用全部的训练集，每次取训练集的一个subset做训练，这样虽然用的是同一个机器学习算法但是得到的模型是不一样的；同时，因为我们没有一份子数据集是全的，因此即使出现过拟合，也是在子训练集上出现过拟合，而不是在全体数据上，这样做一个融合对结合会有很大的帮助，这就是常用的Bagging.

#模型融合
from sklearn.ensemble import BaggingRegressor
train_df=df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
train_np=train_df.as_matrix()
y=train_np[:,0]
X=train_np[:,1:]

#fit到BaggingRegressor之中
clf3=linear_model.LogisticRegression(C=1.0,penalty='l1',tol=1e-6)
bagging_clf=BaggingRegressor(clf3,n_estimators=20,max_samples=0.8,max_features=1.0,bootstrap=True,bootstrap_features=False,n_jobs=1)
#max_samples从训练集中选取用的训练样本。n_estimators基本估计器的个数，就是你要产生多少个子模型。max_features特征数量
#bootstrap样本是否被替换；bootstrap_features样本特征是否被替换。
bagging_clf.fit(X,y)
print bagging_clf.score(X,y)
test=df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
predictions=bagging_clf.predict(test)

result=pd.DataFrame({'PassengerId':data_test['PassengerId'].as_matrix(),'Survived':predictions.astype(np.int32)})
result.to_csv('lrbp.csv')

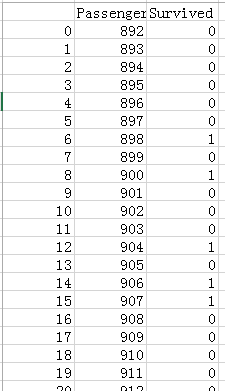
结果如下图：

这样我们就完成预测了。。。