的> 转载请标明出处,谢谢!
https://www.jianshu.com/p/873f2d5b9ca1
关联文章
冒泡、选择排序 https://www.jianshu.com/p/176b0b892591
栈和队列 https://www.jianshu.com/p/8cb602ef4e21
顺序表、单双链表 https://www.jianshu.com/p/3aeb5998e79e
二叉树 https://www.jianshu.com/p/de829eab944c
图论 https://www.jianshu.com/p/cf03e51a3ca2
算法 https://www.jianshu.com/p/873f2d5b9ca1
Lcs算法
动态规划思想
经常会遇到复杂问题不能简单地分解成几个子问题,而会分解出一系列的子问题。简单地采用把大问题分解成子问题,并综合子问题的解导出大问题的解的方法,问题求解耗时会按问题规模呈幂级数增加。
为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组 中,这就是动态规划法采用的基本方法
问题描述
什么是最长公共子序列呢?好比一个数列 S,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则S 称为已知序列的最长公共子序列。
举个例子,如:有两条随机序列,如 1 3 4 5 5 ,and 2 4 5 5 7 6,则它们的最长公共子序列便是:4 5 5。
注意最长公共子串(Longest CommonSubstring)和最长公共子序列(LongestCommon Subsequence, LCS)的区别:子串(Substring)是串的一个连续的部分,子序列(Subsequence)则是从不改变序列的顺序,而从序列中去掉任意的元素而获得的新序列;更简略地说,前者(子串)的字符的位置必须连续,后者(子序列LCS)则不必。比如字符串acdfg同akdfc的最长公共子串为df,而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。
解最长公共子序列问题时最容易想到的算法是穷举搜索法,即对X的每一个子序列,检查它是否也是Y的子序列,从而确定它是否为X和Y的公共子序列,并且在检查过程中选出最长的公共子序列。X和Y的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列,因此,X共有2m个不同子序列(Y亦如此,如为2n),从而穷举搜索法需要指数时间(2m * 2^n)。考虑到搜索性能我们今天引出了一个动态规划算法来解决这个lcs算法的问题。
下面开始举个例子说明:
假设有两个序列分别是X = ABCBDAB,Y = BDCABA
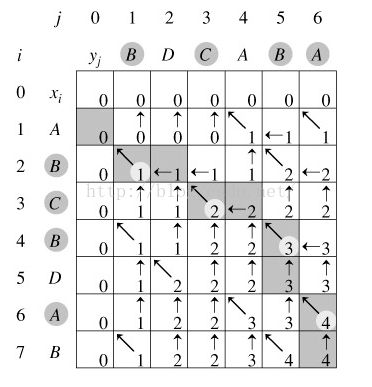
我们通过一个矩阵来说明:
我们可以看到矩阵中有很多数字,暂且先不看灰色背景以及箭头,我们先看下图中矩阵的数字代表的是什么意思呢?
第一行和第一列統一填0,其他的相同的取左上角数字+1,不同的取左边和上边的最大者。
分析完数字的填写规则,现在讨论下灰色数字。我们从右下角的4开始分析,4所在的位置是Yj的A 和Xi的B,A≠B 所以4是左边或者右边推出来的(逆向推出数据)我们选择头部的4继续分析,它的位置是Yj的A 和Xi的A,A=A ,所以它是由左上角的3推出的。继续分析3的由来,3的位置是Yj的B 和Xi的D,B≠D。所以它是由头部的3推出的。。。。。以此类推。就得到了图中灰色区域。
那么我们要怎么得出他的最长公共子序列呢?
我们通过第一轮已经得到了灰色的区域,我们接下去通过灰色区域去分析:
右下角的4所在的位置表示A、B.因为A≠B.所以舍弃。 头部的4表示的是A和A,他们相等。所以得到一个A。以此类推,我们可以最终得到 A、B、C、B。那么倒序输出就是BCBA,那么他们的最长公共子序列就是BCBA.我们用肉眼去检查下,结果也是对的。
我们一开始分析的位置是最右小角的4,当然你也可以从其他几个4的位置开始。图中箭头表示的就是不同的路径分析的结果。
代码分析:
public void getLCS(String x, String y) {
/*将字符串转为字母保存*/
char[] a = x.toCharArray();
char[] b = y.toCharArray();
/*创建矩阵*/
int[][] array = new int[a.length + 1][b.length + 1];
int column = b.length + 1;
int row = a.length + 1;
/*将第一列、第一行设置0*/
for (int i = 0; i < column; i++) {
array[0][i] = 0;
}
for (int i = 1; i < row; i++) {
array[i][0] = 0;
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < column; j++) {
if(a[i-1]==b[j-1]){//如果相等,左上角加1填入
array[i][j]=array[i-1][j-1]+1;
}else{
array[i][j]=max(array[i-1][j],array[i][j-1]);
}
}
}
//打印
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
以上的操作是根据动态规划的方式填入数据
打印的结果:
和显然和我们一开始矩阵图是相同的
接着将灰色部分的填入并输出相应的字母
Stack result = new Stack();
int i = row - 2;
int j = column -2 ;
while (i>=0 && j>=0){
if(a[i]==b[j]){
/*将当前的字母储存*/
result.push(a[i]);
i--;
j--;
}else{
/*注意数组和String中的位置有一位差*/
if(array[i+1][j+1-1]>array[i+1-1][j+1]){
j--;
}else{
i--;
}
}
}
System.out.println("-----");
while(!result.isEmpty()){
System.out.println(result.pop()+" ");
}
Kmp算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。
字符串匹配。给你两个字符串,寻找其中一个字符串是否包含另一个字符串,如果包含,返回包含的起始位置。
我们用一个简单的例子说明一般的字符串匹配做法(暴力匹配)
以下例子来源:http://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
因为B与A不匹配,搜索词再往后移。
就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
接着比较字符串和搜索词的下一个字符,还是相同。
直到字符串有一个字符,与搜索词对应的字符不相同为止。
这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
一般匹配字符串时,我们从目标字符串str(假设长度为n)的第一个下标选取和ptr长度(长度为m)一样的子字符串进行比较,如果一样,就返回开始处的下标值,不一样,选取str下一个下标,同样选取长度为n的字符串进行比较,直到str的末尾(实际比较时,下标移动到n-m)。这样的时间复杂度是 O(n*m) 。
KMP算法:可以实现复杂度为O(m+n)
为何简化了时间复杂度:
充分利用了目标字符串ptr的性质(比如里面部分字符串的重复性,即使不存在重复字段,在比较时,实现最大的移动量)。
比如我们现在有一个字符串是"ababcabcbababcabacaba"
考察目标字符串ptr:
ababcaba
这里我们要计算一个长度为m的转移函数next。
next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。
比如:abcjkdabc,那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc,最长前缀和最长后缀相同是cbc。
abcbc,最长前缀和最长后缀相同是不存在的。
注意最长前缀:是说以第一个字符开始,但是不包含最后一个字符。
比如aaaa相同的最长前缀和最长后缀是aaa。
对于目标字符串ptr,ababcaba ,长度是8,所以next[0],next[1],next[2],next[3],next[4],next[5],next[6],next[7]分别计算的是
a,ab,aba,abab,ababc,ababca,ababcab,ababcaba 的相同的最长前缀和最长后缀的长度。由于a,ab,aba,abab,ababc,ababca,ababcab,ababcaba 的相同的最长前缀和最长后缀是“”,“”,“a”,“ab”,“”,“a”,“ab”,“aba”,所以next数组的值是[0,0,1,2,0,1,2,3],这里0表示不存在,1,2,3分别代表匹配到的个数。
我们用图例来进一步说明下:
(可以用一个count值统计相同的个数)
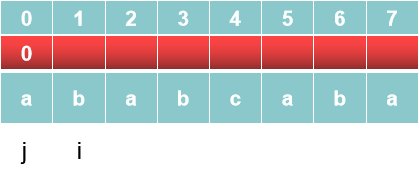
1、我们需要2个指针j 和 i。j指向第一个位置,i指向第二个位置。
默认next[0] = 0
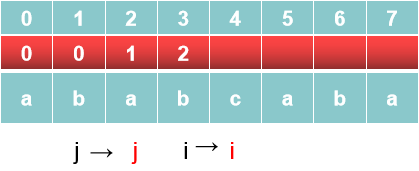
2、因为a≠b,所以b的next值next[1]是=0,此时j直接退回到第一个位置,i往后进一位
3、因为最后一位和第一位的a相等,所以a的next值next[2]是 1,此时count = 1
4、同理b的next值next[3]是 2 , 此时count = 2
5、因为a≠c,所以b的next值next[4]是=0,此时j直接退回到第一个位置,i往后进一位 此时count = 0
6、两个a相等,所以next[5]=1,此时count=1
7、同理对next[6],nexy[7]是同样的操作
那么我得到上面这几个数字的作用是什么呢? 上面我们提过字符串匹配的暴力做法就是逐一匹配,遇到不同的重新回到原来的位置。而kmp算法就是为了尽可能的移动最大偏移量。
我们的原来字符串是 "ababcabcbababcabacaba"
考察目标字符串ptr是:"ababcaba"。
用我们的肉眼几乎一眼就可以看出目标串一直匹配到倒数第二位,直到最后一位a与原字符串的c是不匹配的,所以移动的时候并不需要一位一位的移动。但是计算机毕竟是傻的,他怎么直到要移动多少位置呢?
实际上我们有个规则。
移动位数 = 已匹配的字符数 - 对应的部分匹配值
根据这个规则,我们进行第一次移动。移动位数 = 已匹配的个数7 - 对应部分匹配值b对应的next是2= 5
所以我们需要一次性移动5位。
实际上kmp最核心的就是回退策略。用一句代码表示就是 j = next[j-1].当遇到不同的时候j的指针就回退到该位置。举个例子:刚刚在比对过程中我们发现了a和c是不同的 那么此时比对的j的指针就是 j = next[7-1] = 2.所以我们就开始有了上图的从第二个位置开始重新比对。
等下我们可以用代码来表示。
好了继续上面的移动,上图中我们发现a≠c,根据公式:移动的位数= 2 - 0 = 2;
如果遇到第一个就不匹配的直接后移一位
继续移动一位
逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
代码:
/**
*KMP算法得到数组
*/
public static int[] kmpNext(String dest){
int[] next=new int[dest.length()];
next[0]=0;
//开始推出next
for(int i=1,j=0;i0 && dest.charAt(j) != dest.charAt(i)){
j=next[j-1];
}
//1
if(dest.charAt(i)==dest.charAt(j)){
j++;
}
//2
next[i]=j;
}
return next;
}
从代码上我们可以到 如果是相同的 j++,加上外层的i++就相当于刚刚图例中的两个指针同时后移一位。
如果是不同的j = next[i-1]。
完整代码
@Test
public void addition_isCorrect() throws Exception {
String str="ababcabcbababcabacaba";
String dest="ababcaba";
int[] array=kmpNext(dest);
for (int i = 0; i 0 && dest.charAt(j) != dest.charAt(i)){
j=next[j-1];
}
//1
if(dest.charAt(i)==dest.charAt(j)){
j++;
}
//2
next[i]=j;
}
return next;
}
public static int kmp(String str,String dest,int[] next){
for(int i=0,j=0;i0 && str.charAt(i) != dest.charAt(j)){
j=next[j-1];
}
if(str.charAt(i)==dest.charAt(j)){
j++;
}
if(j==dest.length()){//结束
return i-j+1;
}
}
return 0;
}
输出结果是9,说明在源字符串第几个位置开始匹配到数据。
Floyd算法
Floyd算法(Floyd-Warshall algorithm)又称为弗洛伊德算法、插点法,是解决给定的加权图中顶点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
举个例子说明下:
我们用一个图表示
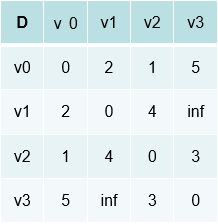
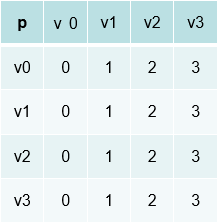
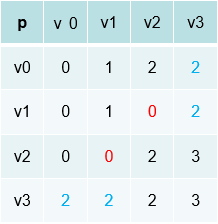
生成他们的邻接矩阵和路径矩阵
其中d矩阵中的inf表示不能直接达到,比如v1->v3
接着我们修改d矩阵,然后把受影响的地方储存在p矩阵中(修改p矩阵中对应的数据)
什么意思呢?
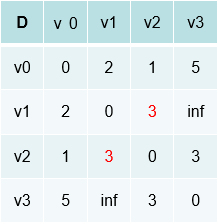
首先我们以v0为跳板,从图中我们可以看出v1->v2直接到达权重是4,如果以v0为跳板我们可以看到,v1->v0是2 v0->v2是1 3<4那么就修改d矩阵
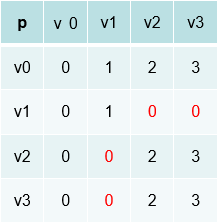
再修改p矩阵,被0矩阵作为跳板修改过,则修改成0.同样的inf位到达的也可以通过v0修改
接着我们以v1为跳板,发现没有要修改的数据
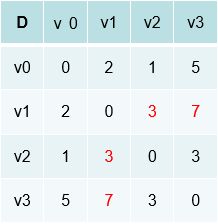
以v2为跳板,我们发现v0->v3 = 5,而v0->v2->v3 = 4 v1->v3=7,而 v1->v2->v3 =6 同样上面修改的原则对d,p矩阵进行修改.
最后v3同样不需要修改。所以以上的图就是最短路径d,p矩阵图
那么这个代码要怎么写呢?其实看懂了逻辑就很简单了。我们先拿v0为跳板的例子:
public static void printArray(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
System.out.println("---------------------");
}
//邻接距阵
public static int[][] d = new int[][]{
{0, 2, 1, 5},
{2, 0, 4, I},
{1, 4, 0, 3},
{5, I, 3, 0}
};
public static int[][] p = new int[][]{
{0, 1, 2, 3},
{0, 1, 2, 3},
{0, 1, 2, 3},
{0, 1, 2, 3}
};
private static void floyd() {
for (int i = 0; i < d.length; i++) {
for (int j = 0; j < d[0].length; j++) {
if (d[i][j] > d[i][0] + d[0][j]) {
d[i][j] = d[i][0] + d[0][j];
p[i][j] = p[i][0];
}
}
}
}
打印的结果是
和我们一开始做的两个矩阵图是一样的
接着只要把0 再外面套个循环修改成动态的就可以了
完整代码是:
public class FloydTest {
private final static int I = Integer.MAX_VALUE;
@Test
public void test() {
floyd();
printArray(d);
printArray(p);
}
public static void printArray(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
System.out.println("---------------------");
}
//邻接距阵
public static int[][] d = new int[][]{
{0, 2, 1, 5},
{2, 0, 4, I},
{1, 4, 0, 3},
{5, I, 3, 0}
};
public static int[][] p = new int[][]{
{0, 1, 2, 3},
{0, 1, 2, 3},
{0, 1, 2, 3},
{0, 1, 2, 3}
};
private static void floyd() {
for (int k = 0; k < d.length; k++) {
for (int i = 0; i < d.length; i++) {
for (int j = 0; j < d[0].length; j++) {
if (d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
p[i][j] = p[i][k];
}
}
}
}
}
}
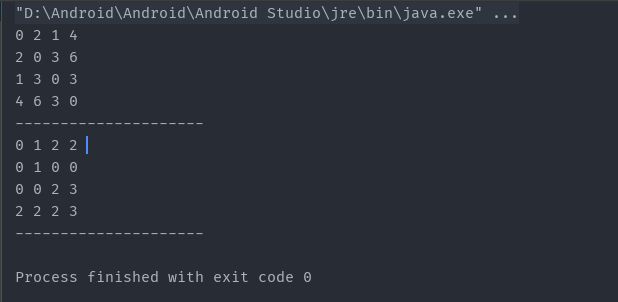
输出的结果是:
Dijkstra算法
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
Dijkstra算法介绍
算法特点:
迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
算法的思路
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T,初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,OK,此时完成一个顶点,
然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
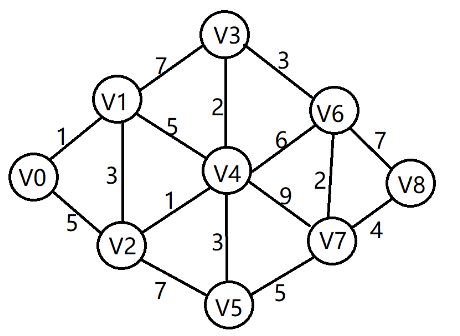
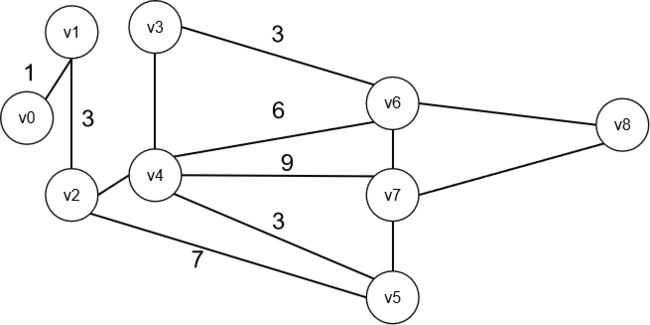
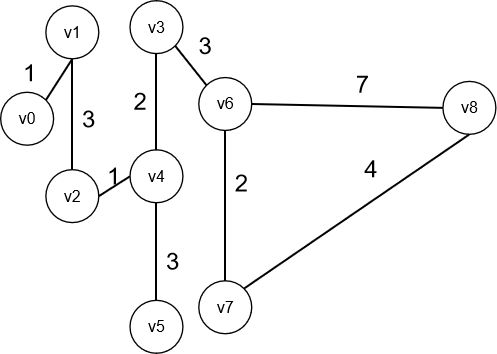
我们用图来表示下算法实现的过程
假设我们有以上这个图,图中的数字表示的是权重。我们用一个矩阵来表示下:
{0,1,5,I,I,I,I,I,I},
{1,0,3,7,5,I,I,I,I},
{5,3,0,I,1,7,I,I,I},
{I,7,I,0,2,I,3,I,I},
{I,5,1,2,0,3,6,I,I},
{I,I,7,I,3,0,I,5,I},
{I,I,I,3,6,I,0,2,7},
{I,I,I,I,9,5,2,0,4},
{I,I,I,I,I,I,7,4,0}
其中数字代表的是权重,I表示无法到达。比如第一行的1,表示的是v0->v1的路径是1,v0->v3无法到达。以此类推。
我们用两个数组表示下:
权重数组、路径数组
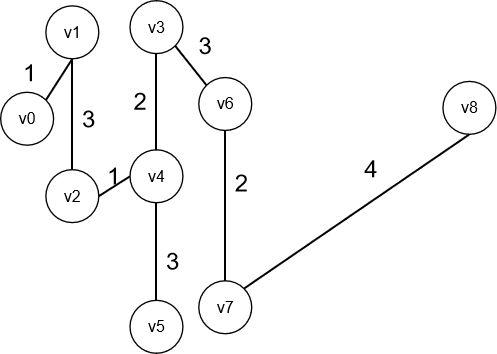
以v0作为定点,v0可以直接到达的是v1和v2,我们选择权重小的v1。
继续,一旦顶点被选择了,就往左边推
图中以v1为例子,v0->v1的权重是1,前驱是v0。
然后从左边到右边我们可以看到v1-v2是最小路径,故删除入度到v2比较大的路径:
继续往下操作,以下直接贴图。
选择v4
选择v3
选择5或6,这里我们选择5
选择6
选择7
最后剩一个8
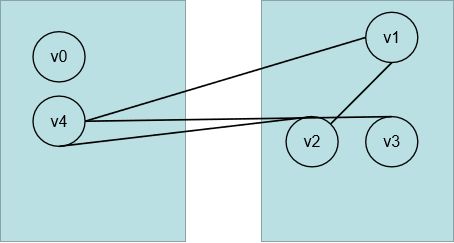
以上就是Dijkstra思想的图例,如果还不懂,我们用一个简单的图和一些简答的描述来说明, Dijkstra的核心算法计算最短路径实际上就是不断选择一个最短的路径顶点归到左边,如下图
比如v0到v4是最短的,那么把v4标记成已选择放入左边
然后重新计算出各个权重,最后不断的选择出最短路径归入左边已选择的数组中。所以这个就是他的核心思想,通过这个思想我们可以通过代码来表示
代码:
public static final int I = 100;
int[][] array=new int[][]{
{0,1,5,I,I,I,I,I,I},
{1,0,3,7,5,I,I,I,I},
{5,3,0,I,1,7,I,I,I},
{I,7,I,0,2,I,3,I,I},
{I,5,1,2,0,3,6,I,I},
{I,I,7,I,3,0,I,5,I},
{I,I,I,3,6,I,0,2,7},
{I,I,I,I,9,5,2,0,4},
{I,I,I,I,I,I,7,4,0}
};
public void dijkstar(){
int k=0;//表示当前正要处理的顶点Vk
//初始化相关的信息
int[] path=new int[9];//保存路径
int[] weight=array[0];//保存权重
//定义一个数组来存放U和V两个集合的信息
int[] flag=new int[9];
flag[0]=1;
//开始逻辑,求VO到某个顶点的最短路径
for(int v=1;v<9;v++){
//在能走的路径中找到最短的一条
int min=I;
for(int i=0;i<9;i++){
if(flag[i]==0 && weight[i]