最多连续数的子集

给一个整数数组a[]， 找到其中包含最多连续数的子集，比如给：15, 7, 12, 6, 14, 13, 9, 11，则返回: 5:[11, 12, 13, 14, 15] 。

最简单的方法是sort然后scan一遍，但是要 o(nlgn) ， 有什么 O(n) 的方法吗？

思路：

网上有人用map来做，个人觉得用map的复杂度还是O(nlgn)。并查集可以做到O(n)，但网上一直没有看到完整的代码，所以自己写了一个。

先简单介绍并查集的内容，算法导论和网上都可以找到相应的资料。

并查集是一宗简单的用途广泛的算法和数据结构。并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作。应用很多，比如：求无向图的连通分量个数，实现kruskal算法等。

并查集可以方便地进行以下三种操作：

1、Make(x)：把每一个元素初始化为一个集合，初始化后每一个元素的父节点就是它本身。

2、Find(x)：查找一个元素所在的集合，一个元素所在的集合用这个集合的祖先节点来标识。判断两个元素是否属于同一个集合，只要看他们所在集合的祖先节点是否相同即可。

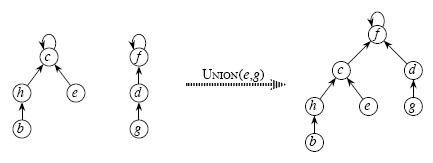
3、Union(x, y)：合并x、y所在的两个集合，先利用Find()找到两个集合的祖先，若这两个祖先节点不是同一个节点，将其中一个祖先节点指向另一个祖先节点即可。（具体哪个祖先指向哪个祖先可以根据实际情况而定）如图：

并查集的优化：在Find函数中，每次找祖先节点的复杂度是O(n)。当我们经过递归找祖先节点的时候，顺便把这条路径上的所有子孙节点都直接指向祖先，这样下次Find的时候复杂度就变成了O(1)。

回到题目，首先调用Make(x)将每个元素变成一个并查集，然后一次扫描a[i]，查看a[i]-1是否存在，若存在调用Union(a[i], a[i]-1)；查看a[i]+1是否存在，若存在调用Union(a[i]+1, a[i])。在合并的同时更新集合的大小。接下里的问题是怎么判断a[i]-1和a[i]+1是否存在，用哈希可以解决，而且复杂度是O(1)。

该题中并查集的操作都是基于下标的。我们用p[i]表示a[i]的父节点的下标，用len[i]表示以a[i]为根的集合的大小，我们合并的时候总是将较小值集合的祖先指向较大值集合的祖先，这样就只需要记录较大值集合的祖先节点对应的长度。最后扫描数组a[]和len[]，找到最大长度maxLen对应的a[i]。最后的结果就是：a[i]-maxLen+1, a[i]-maxLen+2, ..., a[i]。

#include 
#include 
#include 
using namespace std;

void Make(vector& p, vector& len, int x)
{
	p[x] = x;		//x是下标
	len[x] = 1;		//一个节点的集合长度为1
}

int Find(vector& p, int x)
{
	if (x != p[x])
		p[x] = Find(p, p[x]);	//路径压缩，将该路径上所有子孙节点，即集合中所有子孙节点的父节点都为根节点
	return p[x];
}

void Union(vector& p, vector& len, int x, int y)
{//传参的时候，要将较大值的节点传给x，较小值的节点传给y
	int px = Find(p, x);
	int py = Find(p, y);
	if (px == py)
		return;
	p[py] = px;			//将py指向px
	len[px] += len[py];	//px为新的祖先，px的值要大于py的值，所以只更新px的长度即可
}

void Longest(vector& ivec, int& max, int& maxLen)
{
	assert(!ivec.empty());
	int size = ivec.size();
	vector p(size);
	vector len(size);
	for (int i = 0; i < size; ++i)
		Make(p, len, i);
	int MAX = ivec[0];
	for (int i = 1; i < size; ++i)
	{
		if (ivec[i] > MAX)
			MAX = ivec[i];
	}
	vector hash((MAX+2), -1);	//用于查找a[i]-1和a[i]+1是否存在
	for (int i = 0; i < size; ++i)
		hash[ivec[i]] = i;

	for (int i = 0; i < size; ++i)
	{
		int num = ivec[i];
		if (hash[num] == i)	//这个判断条件用于处理重复数字，若hash[num]!=i，说明在i之后还有num重复出现，只处理最后一个即可
		{
			if (hash[num-1] != -1)
				Union(p, len, i, hash[num-1]);
			if (hash[num+1] != -1)
				Union(p, len, hash[num+1], i);
		}
	}
	max = ivec[0];
	maxLen = len[0];
	for (int i = 1; i < size; ++i)
	{
		if (len[i] > maxLen)
		{
			maxLen = len[i];
			max = ivec[i];
		}
	}
}

int main()
{
	int a[] = {15, 7, 12, 6, 14, 13, 9, 11};
	vector ivec(a, a + 8);
	int max, maxLen;
	Longest(ivec, max, maxLen);
	for (int i = max-maxLen+1; i <= max; ++i)
		cout << i << ' ';
	cout << endl;
	return 0;
}