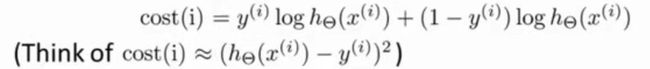机器学习(4)--前向神经网络及BP算法
吴恩达ML课程课后总结,以供复习、总结、温故知新,也欢迎诸位评论讨论分享,一起探讨一起进步:
上一篇:机器学习(3)--正则化及python源码(附练习数据资源文件百度云)https://blog.csdn.net/qq_36187544/article/details/88060700
下一篇:机器学习(4)--前向神经网络及BP算法 python实现(附练习数据资源文件百度云)https://blog.csdn.net/qq_36187544/article/details/88300086
终于到较著名的算法了,BP算法--back propagation,反向传播算法。
之前的LR算法是一种典型的分类算法,但是当特征数量较大且有一定相关性时,使用LR算法求解复杂度急剧上升,比如100个变量,罗列所有二次项,比如X1X1,X1X2...,O(n^2) ,若是所有三次项复杂度就成了O(n^3)
总而言之,若是非线性的问题,再用LR算法求解很难找到最合适的函数模型。比如,在CV(计算机视觉)中,机器识别图片解码的数字矩阵,一张100*100像素的灰度图片(RGB有3万特征)就有一万个特征,这样对于LR算法负荷太重了
神经网络模拟自然界生物脑子的神经网络,由错综复杂的网络组成,神经元是其基本节点,通过突触连接,形成复杂网络。
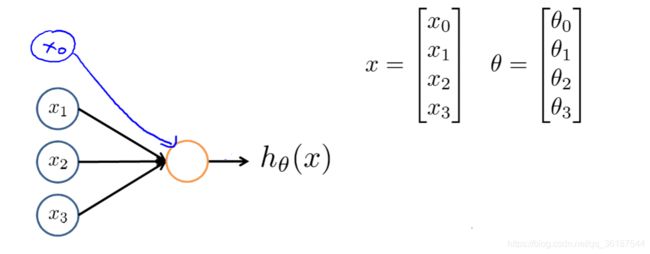
下图是一个简单神经元模型,输入是X1,X2,X3,手动添加X0作为偏置单元(又叫截距),X与输出之间用θ作为参数(也叫权重),构造出函数g(z),可以用logistics Unit作为神经单元(或者叫激活函数),z=θTx=θ0×X0+θ1×X1+θ2×X2+θ3×X3。当然也可用其他的作为神经元。通常令偏置单元为1
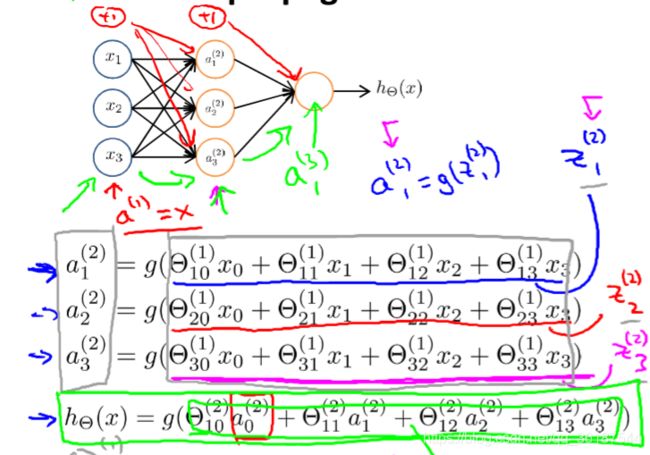
神经网络可以形如下图,x1,x2,x3是输入层,而h(x)是输出层,除此之外其余所有层为中间层(隐藏层):
通过这种结构可以发现,第二层是第一层的函数结果,而第三层又是第二层的函数结果,这样就让变量可以是非线性关系,从而得到更加优化的结果。
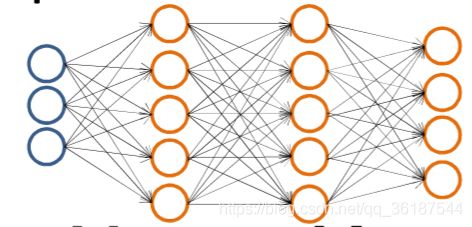
如果想让神经网络有一个多元输出,可以让神经网络输出多个,下图有4个输出,可以定义[1,0,0,0]是一种输出,[0,1,0,0]是另一种等,若只有一个输出神经元,则属于二分类。
接下来的内容,就是如何实现神经网络:
下图是代价函数的表达,一个是逻辑回归的代价函数,一个是神经网络的代价函数,K表示输出单元的数量(二分类问题K=1),m表示输入的特征数量,sl是每层网络的神经元数量,如s1表示输入层神经元个数(不包括偏置单元)。在算式最后3个求和Σ中,这一项相当于正则化项,有sl,s(l+1)即两层神经元之间对应关系,正则化项所以从j=1开始而不是从0,同逻辑回归中θ0的处理一样。L表示神经网络层数(包括输入层和输出层)
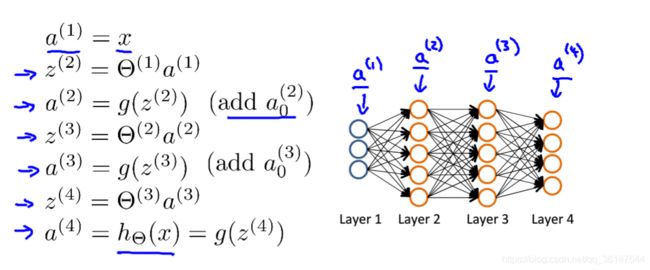
进行前向传播计算时,如下,层层计算输出即可:
前向传播能够确定单次的输出,但是如何改变优化权重(参数)就需要用到反向传播算法,算法如下:
.*代表矩阵的点乘,实际上a=g(z)是Sigmoid函数,求导可得g'(z)=a·(1-a)。
程序方法如下,不断更新△的值,加上正则化更新Dij:
这些公式究竟是如何得来的?
首先近似把代价函数看为得到的值与实际值的方差:
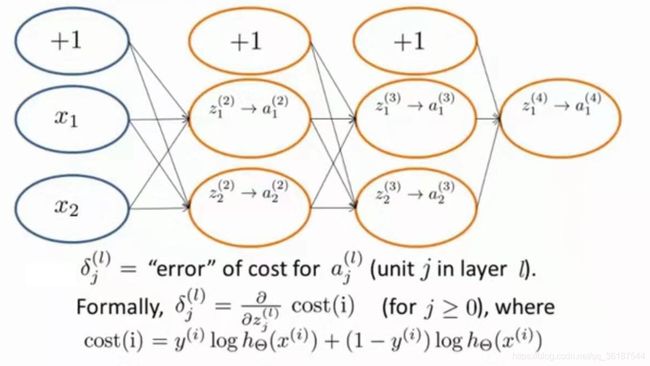
在前向网络中,误差是累积的,所以δ实际含义为代价函数关于中间项的加权和,就是高等数学中的链式法则
这是一个反向传播的计算过程,从输出层开始反向向输入层传播
一点个人理解:前向传播是一种计算方式(虽然也说它是一种算法,但是这种算法停留在计算的层面,不能产生实质),反向传播是一种优化传递参数的算法,反向传播算法在使用时会运用上前向传播计算
对于反向传播容易产生微妙的bug,看起来计算正常,使用方法梯度检验。双侧差分计算导数,若计算出结果与导数相差几位小数,认为反向传播正确。先写反向传播,再写梯度检验,检验完之后关闭梯度检验
梯度检验如下,即计算双侧差分值与导数的差别,若在小差别(可设置为10的-4次方)之内,认为其收敛
除此之外,要注意初始化的问题:
初始化θ时不要全部置0会导致权重完全等价,最后结果完全一致。一般用初始化为【-ε,ε】初始化为一个趋近于0的数,但是不完全一致,避免导致最后所有权重同步更新。(同步更新的思想可采用对称的思想考虑,X1,X2两个输入,第二层都要用到X1,X2所以导致权重一起变大,一起变小)
总步骤:
0.确定一个神经模型,几层几个神经元等,隐藏层的神经元个数一般等于输入特征数的1-4倍。
1.初始化权重θ。
2.执行一次前向算法,得到一次输出y的向量。
3.计算代价函数。
4.反向传播计算偏导(for循环时前向和反向)。
5.梯度检验,记得关闭。
6.结合其他优化算法最小化代价函数
可能收敛到局部最小值,但是不是问题,基本效果都挺好