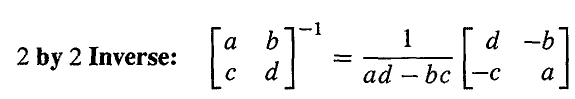线性代数之——矩阵乘法和逆矩阵
1. 矩阵乘法
如果矩阵 B B B 的列为 b 1 , b 2 , b 3 b_1, b_2, b_3 b1,b2,b3,那么 E B EB EB 的列就是 E b 1 , E b 2 , E b 3 Eb_1, Eb_2, Eb_3 Eb1,Eb2,Eb3。
E B = E [ b 1 b 2 b 3 ] = [ E b 1 E b 2 E b 3 ] \boldsymbol{EB = E[b_1 \quad b_2 \quad b_3] = [Eb_1 \quad Eb_2 \quad Eb_3]} EB=E[b1b2b3]=[Eb1Eb2Eb3]
E ( B 的 第 j 列 ) = E B 的 第 j 列 E\space(B 的第\space j \space列) =EB \space的第 \space j \space列 E (B的第 j 列)=EB 的第 j 列
- 置换矩阵(permutation matrix)
在消元的过程中,如果遇到了某一行主元的位置为 0,而其下面一行对应的位置不为 0,我们就可以通过行交换来继续进行消元。
如下的矩阵 P 23 P_{23} P23 可以实现将向量或者矩阵的第 2 、 3 行进行交换。
P 23 = [ 1 0 0 0 0 1 0 1 0 ] P_{23} = \begin{bmatrix} 1&0&0 \\ 0&0&1\\0&1&0\end{bmatrix} P23=⎣⎡100001010⎦⎤
[ 1 0 0 0 0 1 0 1 0 ] [ 1 3 5 ] = [ 1 5 3 ] \begin{bmatrix} 1&0&0 \\ 0&0&1\\0&1&0\end{bmatrix} \begin{bmatrix} 1 \\ \boldsymbol 3\\\boldsymbol 5\end{bmatrix} = \begin{bmatrix} 1 \\ \boldsymbol 5\\\boldsymbol 3\end{bmatrix} ⎣⎡100001010⎦⎤⎣⎡135⎦⎤=⎣⎡153⎦⎤
[ 1 0 0 0 0 1 0 1 0 ] [ 2 4 1 0 0 3 0 6 5 ] = [ 2 4 1 0 6 5 0 0 3 ] \begin{bmatrix} 1&0&0 \\ 0&0&1\\0&1&0\end{bmatrix} \begin{bmatrix} 2&4&1 \\ \boldsymbol0&\boldsymbol0&\boldsymbol3\\0&6&5 \end{bmatrix} = \begin{bmatrix} 2&4&1 \\0&6&5 \\\boldsymbol0&\boldsymbol0&\boldsymbol3\end{bmatrix} ⎣⎡100001010⎦⎤⎣⎡200406135⎦⎤=⎣⎡200460153⎦⎤
置换矩阵 P i j P_{ij} Pij 就是将单位矩阵的第 i i i 行和第 j j j 行进行互换,当交换矩阵乘以另一个矩阵时,它的作用就是交换那个矩阵的第 i i i 行和第 j j j 行。
- 增广矩阵(augmented matrix)
在消元的过程中,方程两边的系数 A A A 和 b b b 都要进行同样的变换,这样,我们可以把 b b b 作为矩阵 A A A 的额外的一列,然后,就可以用消元矩阵 E E E 乘以这个增广的矩阵一次性完成左右两边的变换。
E [ A b ] = [ E A E b ] E[A \space \boldsymbol b] = [EA \space E \boldsymbol b] E[A b]=[EA Eb]
[ 1 0 0 − 2 1 0 0 0 1 ] [ 2 4 − 2 2 4 9 − 3 8 − 2 − 3 7 1 0 ] = [ 2 4 − 2 2 0 1 1 4 − 2 − 3 7 1 0 ] \begin{bmatrix} 1&0&0 \\ -2&1&0\\0&0&1\end{bmatrix} \begin{bmatrix} 2&4&-2&\boldsymbol 2 \\ 4&9&-3&\boldsymbol 8 \\-2&-3&7&\boldsymbol 10 \end{bmatrix} = \begin{bmatrix} 2&4&-2&\boldsymbol 2 \\ 0&1&1&\boldsymbol 4 \\-2&-3&7&\boldsymbol 10 \end{bmatrix} ⎣⎡1−20010001⎦⎤⎣⎡24−249−3−2−372810⎦⎤=⎣⎡20−241−3−2172410⎦⎤
- 矩阵乘法的四种理解
如果矩阵 A A A 有 n n n 列, B B B 有 n n n 行,那么我们可以进行矩阵乘法 A B AB AB。
假设矩阵 A A A 有 m m m 行 n n n 列,矩阵 B B B 有 n n n 行 p p p 列,那么 A B AB AB 是 m m m 行 p p p 列的。
( m × n ) ( n × p ) ( m × p ) [ m 行 n 列 ] [ n 行 p 列 ] [ m 行 p 列 ] (m×n)(n×p)(m×p) \quad \begin{bmatrix} \boldsymbol{m \space 行} \\{n \space 列} \end{bmatrix} \begin{bmatrix} n \space 行 \\\boldsymbol{p \space 列} \end{bmatrix} \begin{bmatrix} \boldsymbol{m \space 行} \\\boldsymbol{p \space 列}\end{bmatrix} (m×n)(n×p)(m×p)[m 行n 列][n 行p 列][m 行p 列]
矩阵乘法的第一种理解方式就是一个一个求取矩阵 A B AB AB 位于 ( i , j ) (i, j) (i,j) 处的元素
( A B ) i j = A 的 第 i 行 与 B 的 第 j 列 的 内 积 = ∑ a i k b k j (AB)_{ij} = A \space 的第 \space i \space 行与\space B \space的第\space j \space 列的内积 = \sum a_{ik}b_{kj} (AB)ij=A 的第 i 行与 B 的第 j 列的内积=∑aikbkj
第二种理解,矩阵 A B AB AB 的列是 A A A 的列的线性组合
A B = A [ b 1 b 2 ⋯ b p ] = [ A b 1 A b 2 ⋯ A b p ] {AB = A[b_1 \quad b_2 \cdots b_p] = [Ab_1 \quad Ab_2 \cdots Ab_p]} AB=A[b1b2⋯bp]=[Ab1Ab2⋯Abp]
第三种理解,矩阵 A B AB AB 的行是 B B B 的行的线性组合
A B = [ a 1 a 2 ⋮ a m ] B = [ a 1 B a 2 B ⋮ a m B ] AB = \begin{bmatrix}a_1 \\ a_2 \\ \vdots \\a_m\end{bmatrix}B = \begin{bmatrix}a_1 B \\ a_2B \\ \vdots \\a_m B\end{bmatrix} AB=⎣⎢⎢⎢⎡a1a2⋮am⎦⎥⎥⎥⎤B=⎣⎢⎢⎢⎡a1Ba2B⋮amB⎦⎥⎥⎥⎤
第四种理解,矩阵 A B AB AB 是所有 A A A 的列与 B B B 的行的乘积的和
A B = [ a 1 a 2 ⋯ a n ] [ b 1 b 2 ⋮ b n ] = ∑ i = 1 n a i b i AB = [a_1 \quad a_2 \cdots a_n] \begin{bmatrix}b_1 \\ b_2 \\ \vdots \\b_n\end{bmatrix} = \sum_{i=1}^{n} a_i b_i AB=[a1a2⋯an]⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤=i=1∑naibi
其中,一列乘以一行称为外积(outer product),(n×1)(1×n)=(n, n),结果为一个 n×n 的矩阵。
[ 2 7 3 8 4 9 ] [ 1 6 0 0 ] = [ 2 3 4 ] [ 1 6 ] + [ 7 8 9 ] [ 0 0 ] = [ 2 12 3 18 4 24 ] \begin{bmatrix}2&7 \\ 3&8 \\ 4&9\end{bmatrix} \begin{bmatrix}1&6 \\ 0&0\end{bmatrix} = \begin{bmatrix}2 \\ 3 \\ 4\end{bmatrix}[1 \quad 6] + \begin{bmatrix}7 \\ 8 \\ 9\end{bmatrix}[0 \quad 0] = \begin{bmatrix}2&12 \\ 3&18 \\ 4&24\end{bmatrix} ⎣⎡234789⎦⎤[1060]=⎣⎡234⎦⎤[16]+⎣⎡789⎦⎤[00]=⎣⎡234121824⎦⎤
- 矩阵乘法的性质
结合律: A ( B C ) = ( A B ) C \boldsymbol{A(BC) = (AB)C} A(BC)=(AB)C
交换律: ( A + B ) C = A C + B C \boldsymbol{(A+B)C = AC+BC} (A+B)C=AC+BC
交换律: A ( B + C ) = A B + A C \boldsymbol{A(B+C) = AB+AC} A(B+C)=AB+AC
A p = A A ⋯ A ⎵ p 个 A^p = \underbrace{AA\cdots A}_{\text{p 个}} Ap=p 个 AA⋯A
A p A q = A ( p + q ) A^pA^q = A^{(p+q)} ApAq=A(p+q)
( A p ) q = A p q (A^p)^q = A^{pq} (Ap)q=Apq
A 0 = I A^0=I A0=I
- 分块矩阵
矩阵还可以被划分为小块,其中每个小块都是一个更小的矩阵。
如果对矩阵 A A A 的列的划分和对矩阵 B B B 的行的划分正好匹配,那么每个块之间就可以进行矩阵乘法。
一种特殊的划分就是矩阵 A A A 的每个小块都是 A A A 的一列,矩阵 B B B 的每个小块都是 B B B 的一行,这种情况就是我们上面说的矩阵相乘的第四种理解。
同样地,在消元的时候,我们也可以按块对系数矩阵进行消元。
2. 矩阵的逆
假设 A A A 是一个方阵,如果存在一个矩阵 A − 1 A^{-1} A−1,使得
A − 1 A = I 并 且 A A − 1 = I A^{-1}A = I \quad 并且 \quad AA^{-1} = I A−1A=I并且AA−1=I
那么,矩阵 A A A 就是可逆的, A − 1 A^{-1} A−1 称为 A A A 的逆矩阵。
逆矩阵的逆就是进行和原矩阵相反的操作。消元矩阵 E 21 E_{21} E21 的作用是第二个方程减去第一个方程的 2 倍。
E 21 = [ 1 0 0 − 2 1 0 0 0 1 ] E_{21} = \begin{bmatrix} 1&0&0 \\ -2&1&0\\0&0&1\end{bmatrix} E21=⎣⎡1−20010001⎦⎤
其逆矩阵 E 21 − 1 E_{21}^{-1} E21−1 的作用则是第二个方程加上第一个方程的 2 倍。
E 21 − 1 = [ 1 0 0 2 1 0 0 0 1 ] E_{21}^{-1} = \begin{bmatrix} 1&0&0 \\ 2&1&0\\0&0&1\end{bmatrix} E21−1=⎣⎡120010001⎦⎤
-
当且仅当在消元过程中产生 n n n 个主元的时候(允许行交换),矩阵 A A A 的逆才存在。
-
矩阵 A A A 不可能有两个不同的逆矩阵,左逆等于右逆。假设 B A = I BA=I BA=I, A C = I AC=I AC=I,那么一定有 B = C B=C B=C。
B ( A C ) = ( B A ) C → B I = I C → B = C B(AC) = (BA)C \to BI = IC \to B=C B(AC)=(BA)C→BI=IC→B=C -
如果矩阵 A A A 是可逆的,那么 A x = b Ax=b Ax=b 有唯一解 x = A − 1 b x=A^{-1}b x=A−1b。
-
如果存在一个非零向量 x x x 使得 A x = 0 Ax= \boldsymbol 0 Ax=0,那么 A A A 不可逆,因为没有矩阵可以将零向量变成一个非零向量。
若 A − 1 存 在 , 则 x = A − 1 0 = 0 若 \space A^{-1} \space 存在,则\space x = A^{-1} \boldsymbol 0 = \boldsymbol 0 若 A−1 存在,则 x=A−10=0
- 一个 2×2 的矩阵是可逆的,当且仅当 a d − b c ad-bc ad−bc 非零。
- 一个对角化矩阵如果其对角线上元素非零,那么其有逆矩阵。
如果矩阵 A A A 和矩阵 B B B 都是可逆的,那么它们的乘积 A B AB AB 也是可逆的。
( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1}A^{-1} (AB)−1=B−1A−1
( A B ) − 1 A B = B − 1 A − 1 A B = B − 1 I B = I (AB)^{-1}AB = B^{-1}A^{-1}AB = B^{-1}IB = I (AB)−1AB=B−1A−1AB=B−1IB=I
同样地,针对三个或更多矩阵的乘积,有
( A B C ) − 1 = C − 1 B − 1 A − 1 (ABC)^{-1} = C^{-1}B^{-1}A^{-1} (ABC)−1=C−1B−1A−1
3. 高斯-若尔当消元法(Gauss-Jordan Elimination)求矩阵的逆
我们可以通过消元法来求解矩阵 A A A 的逆矩阵。思路是这样的,假设 A A A 是一个 3×3 的矩阵,那么我们可以建立三个方程来分别求出 A − 1 A^{-1} A−1 的三列。
A A − 1 = A [ x 1 x 2 x 3 ] = [ e 1 e 2 e 3 ] = [ 1 0 0 0 1 0 0 0 1 ] AA^{-1} = A[x_1 \quad x_2 \quad x_3] = [e_1 \quad e_2 \quad e_3]=\begin{bmatrix} 1&0&0 \\ 0&1&0\\0&0&1\end{bmatrix} AA−1=A[x1x2x3]=[e1e2e3]=⎣⎡100010001⎦⎤
A x 1 = e 1 A x 2 = e 2 A x 3 = e 3 \begin{alignedat}{2} Ax_1 = e_1 \\ Ax_2 = e_2\\ Ax_3 = e_3 \end{alignedat} Ax1=e1Ax2=e2Ax3=e3
而高斯-若尔当消元法则是一次性求解出这些方程,之前我们求解一个方程的时候,将 b b b 作为 A A A 的一列组成增广矩阵,而现在我们则是把 e 1 、 e 2 、 e 3 e_1、e_2、e_3 e1、e2、e3 三列一起放入 A A A 中形成一个增广矩阵,然后进行消元。
到这里,我们已经得到了一个下三角矩阵 U U U,高斯就会停在这里然后用回带法求出方程的解,但若尔当将会继续进行消元,直到得到简化阶梯形式(reduced echelon form)。
最后,我们将每行都除以主元得到新的主元都为 1,此时,增广矩阵的前一半矩阵就是 I I I,而后一半矩阵就是 A − 1 A^{-1} A−1。
我们用分块矩阵就可以很容易地理解高斯-若尔当消元法,消元的过程就相当于乘以了一个 A − 1 A^{-1} A−1 将 A A A 变成了 I I I,将 I I I 变成了 A − 1 A^{-1} A−1。
A − 1 [ A I ] = [ I A − 1 ] A^{-1}[A \quad I] = [I \quad A^{-1}] A−1[AI]=[IA−1]
获取更多精彩,请关注「seniusen」!
![]()