10.3 听说这套题很简单
T1 叫第二题的第一题
直接算就好。
emmm。。我的方法是把第一个日期往后取整,再把第二个日期往前取整,最后答案加上两个日期中间的日期差qwq。
代码
#includeif(i%4==0&&i%100!=0) c+=366;
else if(i%400==0) c+=366;
else c+=365;
}
return c*24*60*60*1000;
}
ll month(int a,int b,int k)
{
ll c=0;
for(int i=a;iif(i==2&&k) ++c;
}
return c*24*60*60*1000;
}
ll day(int a,int b)
{
ll c=b-a;
return c*24*60*60*1000;
}
ll hour(int a,int b)
{
ll c=b-a;
return c*60*60*1000;
}
ll minute(int a,int b)
{
ll c=b-a;
ll k=c*60*1000;
return k;
}
ll second(int a,int b)
{
return (b-a)*1000;
}
int main()
{
freopen("two.in","r",stdin);
freopen("two.out","w",stdout);
gets(s);
int l=strlen(s),num=0;
for(int i=0;i<=l;++i)
{
if(s[i]>='0'&&s[i]<='9') num=num*10+s[i]-'0';
else{
if(Y1==-1) Y1=num;
else if(m1==-1) m1=num;
else if(d1==-1) d1=num;
else if(h1==-1) h1=num;
else if(M1==-1) M1=num;
else if(s1==-1) s1=num;
num=0;
}
}
gets(s);
l=strlen(s),num=0;
for(int i=0;i<=l;++i)
{
if(s[i]>='0'&&s[i]<='9') num=num*10+s[i]-'0';
else{
if(Y2==-1) Y2=num;
else if(m2==-1) m2=num;
else if(d2==-1) d2=num;
else if(h2==-1) h2=num;
else if(M2==-1) M2=num;
else if(s2==-1) s2=num;
num=0;
}
}
ll num1=0,num2=0,k1=0,k2=0;
if(Y1%4==0&&Y1%100!=0) k1=1;
if(Y1%400==0) k1=1;
if(Y2%4==0&&Y2%100!=0) k2=1;
if(Y2%400==0) k2=1;
if(Y1!=Y2)
{
num1=second(0,s1)+minute(0,M1)+hour(0,h1)+day(1,d1)+month(1,m1,k1);
num1=year(Y1,Y1+1)-num1;
num2=second(0,s2)+minute(0,M2)+hour(0,h2)+day(1,d2)+month(1,m2,k2);
ans=num2+num1+year(Y1+1,Y2);
}
else{
if(m1!=m2)
{
num1=second(0,s1)+minute(0,M1)+hour(0,h1)+day(1,d1);
num1=month(m1,m1+1,k1)-num1;
num2=second(0,s2)+minute(0,M2)+hour(0,h2)+day(1,d2);
ans=num1+num2+month(m1+1,m2,k2);
}
else{
if(d1!=d2)
{
num1=second(0,s1)+minute(0,M1)+hour(0,h1);
num1=day(d1,d1+1)-num1;
num2=second(0,s2)+minute(0,M2)+hour(0,h2);
ans=num1+num2+day(d1+1,d2);
}
else{
if(h1!=h2)
{
num1=second(0,s1)+minute(0,M1);
num1=hour(h1,h1+1)-num1;
num2=second(0,s2)+minute(0,M2);
ans=num1+num2+hour(h1+1,h2);
}
else{
if(M1!=M2)
{
num1=second(0,s1);
num1=minute(M1,M1+1)-num1;
num2=second(0,s2);
ans=num1+num2+minute(M1+1,M2);
}
else{
if(s1!=s2){
ans=second(s1,s2);
}
}
}
}
}
}
printf("%lld",ans);
return 0;
} T2 你做过接水问题吗?
请百度 codevs 接水问题。
贪心,每次从堆中弹出当前打sif总时间最小的那个位置,加上当前人所用的时间再扔进去。
#includevector,greater > q;
int main()
{
freopen("death.in","r",stdin);
freopen("death.out","w",stdout);
scanf("%d%d",&N,&M);
for(int i=1;i<=N;++i)
{
scanf("%d",&time[i]);
if(i<=M) q.push(time[i]);
}
if(M>N)
{
printf("%d",0);
return 0;
}
for(int i=M+1;i<=N;++i)
{
ll a=q.top();
q.pop();
a+=time[i];
q.push(a);
}
ll a=q.top();
printf("%lld",a);
return 0;
} T3 出题人想要的不是dp
首先,这并不是一个dp题,而是一个贪心题。(dp会T)
首先说一下dp。
可以打一个裸的01背包问题。因为只有1 * 3和1 * 2的物品,所以在数量都够的前提下,我们是可以一直往里塞直到背包全部填满或是只剩下一个空为止。数量不够的话也可以一直往里填。貌似是正确的。
虽然这道题dp可以水到60分,但是其实是有反例的。(不知道为什么没有被卡)
如:
1
2 5 0 3
3 4 5
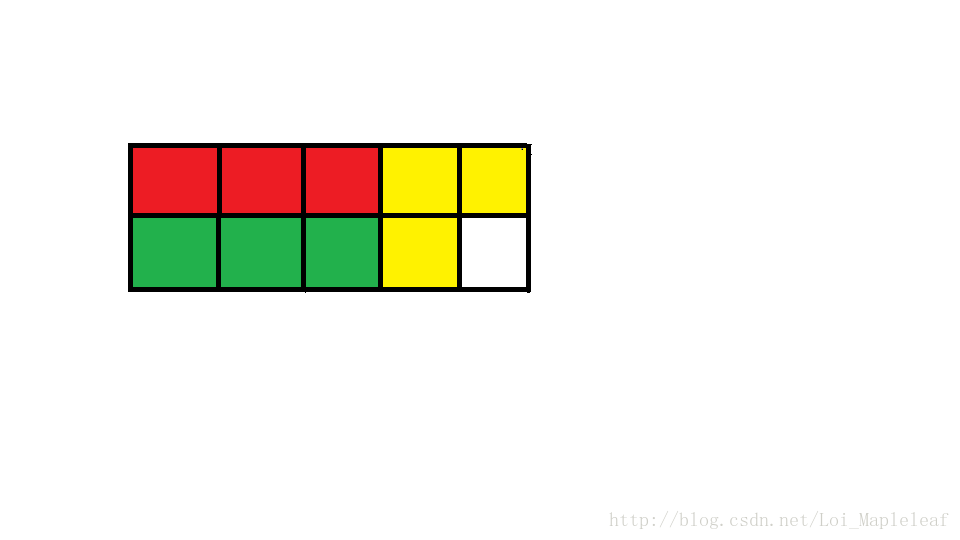
dp输出12,但答案其实是9,因为画出来后是这样:
其实这个黄的是没法放进去的,也就是说,如果N或M为2,而另一个%3==2,同时1*2的块又不够的时候,dp是会被卡掉的。
正解 前缀和+枚举
因为数据范围太大 、同时物品的体积只有1 * 2和1 * 3两种情况,考虑枚举更新。
采用前缀和进行优化。先对物品按照价值从大到小排序,再计算可以放入体积为3
的物品的最大数量(因为3很特殊)。注意特判剩余体积为4但是不能放3的情况(也就是上面的反例)。
另外还要注意到所放的最大物品数不能超过你所拥有的物品数。
代码
#include