【数组和字符串】(四) 双指针技巧

目录

四、双指针技巧

4.1 反转字符串

4.2 数组拆分 I

4.3 两数之和 II - 输入有序数组

4.4 移除元素

4.5 最大连续1的个数

4.6 长度最小的子数组

---

四、双指针技巧

情景一：

文章链接：https://leetcode-cn.com/explore/learn/card/array-and-string/201/two-pointer-technique/782/ 

---

4.1 反转字符串

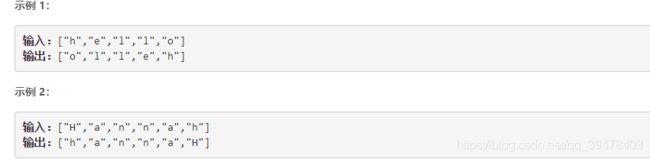
4.1.1 问题描述

4.1.2 求解过程

法一： 依次交换元素，复杂度 O(n)。

2020/06/08 - 89.38% - 次优速度, 最快的还是内建 str.reverse() 

class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        """
        # 不可以使用 s = s[::-1], 因为 s[::-1] 将无法申请新的字符串空间！
        for i in range(len(s)//2):  # 如此将奇偶均可
            s[i], s[-i-1] = s[-i-1], s[i]  # 交换元素, 省去中间变量 temp

        # s.reverse()  # 最快

4.2 数组拆分 I

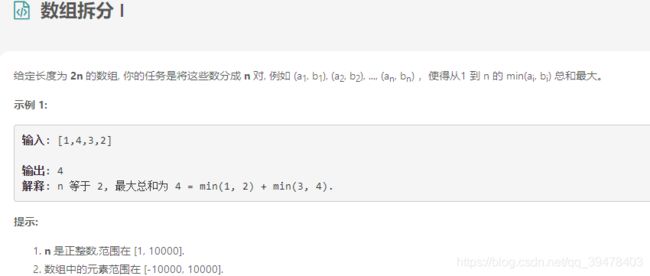
4.2.1 问题描述

4.2.2 求解过程

法一： 先将元素从小到大排序，再对偶数 index 的数字求和。复杂度 O(n)。

2020/06/08 - 99.98% - 基本就是最快的方法了，但是看不出来和双指针有什么关系？！

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        if not nums:
            return 0
        
        nums.sort()  # 元素从小到大排序
        
        # 法一
        summ = 0  
        for i in range(len(nums)//2):  
            summ += nums[2*i]  # 偶数 index 元素求和
        return summ

        #odd_slice = slice(0, len(nums), 2)  
        #return sum(nums[odd_slice])  # 法二

        #return sum(nums[::2])  # 法三 - 消耗内存最少

4.3 两数之和 II - 输入有序数组

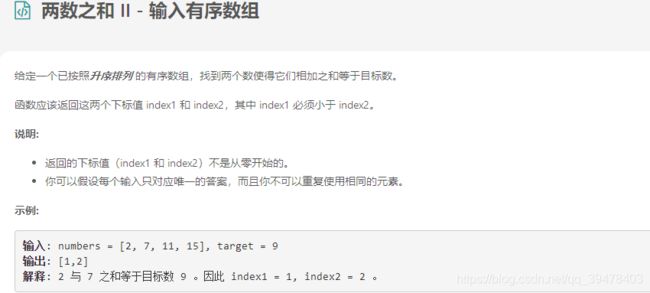
4.3.1 问题描述

4.3.2 求解过程

法一：先找一个上限值约束范围，再进行双指针迭代查找。复杂度 O(n)。

22020/06/08 - 88.66% - 还行！然而似乎存在太多冗余操作了！！

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        former = 0
        latter = len(numbers)-1
        
        if latter == 1:  # 特殊情况 [-1,0] -1
            return [1, 2]
        
        if numbers[-1] >= target:  # 如果列表最大值大于 target
            for index, num in enumerate(numbers):  # 找到比 target 小一点的值 index
                if num > target:
                    latter = index - 1  # 找到了后指针约束范围

        while former <= latter:
            while True:
                if numbers[former] + numbers[latter] == target:
                    return [former+1, latter+1]
                elif numbers[former] + numbers[latter] > target:
                    break
                else:
                    former += 1  # 前指针前进一位
            former = 0   # 前指针复位
            latter -= 1  # 后指针回退一位

法二：参考方法，果然十分地精炼！！无论是循环条件，还是指针调整方式，都比法一要优秀不少！复杂度 O(n)。

2020/06/08 - 99.99% - 值得学习的抽象思维！这才是真正的高效双指针用法！

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        i = 0  # 前指针
        j = len(numbers) - 1  # 后指针
        while numbers[i]+numbers[j] != target:
            if numbers[i]+numbers[j] > target:  # 如果和大于 target, 后指针回退一位
                j -= 1
            elif numbers[i]+numbers[j] < target:  # 如果和小于 target, 前指针前进一位
                i += 1
        return [i+1, j+1]

---

情景二

 文章链接：https://leetcode-cn.com/explore/learn/card/array-and-string/201/two-pointer-technique/786/

---

4.4 移除元素

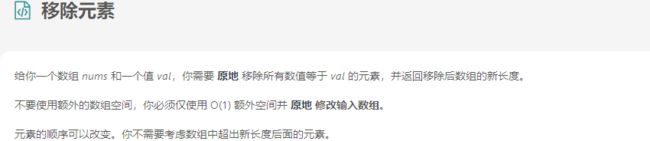
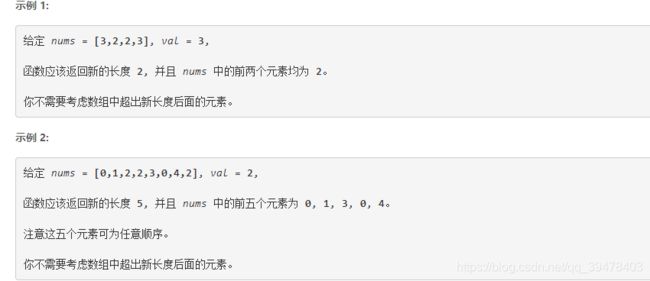
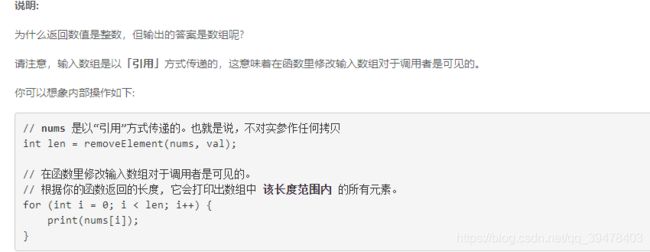
4.4.1 问题描述

4.4.2 求解过程

法一：朴素版快慢指针，复杂度 O(n)。

2020/06/14 - 95.65% - 算最简洁和高效的算法了 —— 快慢指针

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        slow = 0
        for fast in range(len(nums)):
            if nums[fast] != val:
                nums[slow] = nums[fast]  # 慢指针元素指向当前快指针元素
                slow += 1
        return slow

法二：单指针遍历和删除，复杂度 O(n)。但不明白为什么正向会出错，而反向则没问题？

2020/06/14 - 99.9% - 虽然最快，但仅适合 Python，没有算法的思想！

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        for i in range(len(nums)-1, -1, -1):  # 为什么反向可以、正向删除不行？
            if nums[i] == val:
                del nums[i]
        return len(nums)

        #while val in nums:  # 类似的仅追求简洁而没有灵魂的方法
        #    nums.remove(val)
        #return len(nums)

4.5 最大连续1的个数

4.5.1 问题描述

4.5.2 求解过程

法一：普通方法，维护两个计数器，复杂度 O(n)。

2020/06/14 - 99.50% - 基本是最快了的，实际相当于双指针

class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        max_len = nums[0]  # 最大值计数器  # 特殊情况 [1] or [0]
        counter = 0  # 临时值计数器
        for i in range(len(nums)):
            if nums[i]:
                counter += 1
            else:
                max_len = max(max_len, counter)
                counter = 0
                
        if nums[-1] == 1:        
            max_len = max(max_len, counter)  # 特殊情况 最后一个元素是 1 需再更新一次最大值
        
        return max_len

4.6 长度最小的子数组

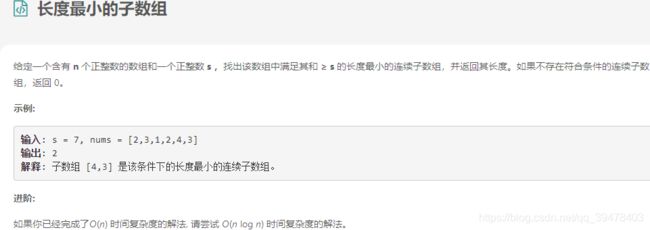
4.6.1 问题描述

4.6.2 求解过程

法一：题目要求连续子数组，故可以使用 双指针 / 对撞指针 动态处理。定义 慢指针 slow 和 快指针 fast，二者之间的数组 (切片) 相当于一个 滑块 / 滑动窗口，如此所有的子数组都会在 索引区间 [slow ... fast] 中出现。若 nums[slow : fast] 的元素之和小于目标值 s，则 fast 向后移一位，再次比较，直到大于目标值 s 后，slow 向前移动一位，缩小子数组 (切片) 长度。每当 nums[slow : fast] 的元素之和大于目标值 s 都会与上一次记录的最小连续子数组长度 min_len 比较并取最小值。当 slow 遍历至数组最末端时结束循环，若不存在符合条件连续子数组将返回 0，否则返回最小子数组长度 min_len。复杂度 O(n)。

2020/06/18 - 98.60% - 还有一点优化空间

class Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        if not nums:  # 特殊情况
            return 0
        
        slow, fast = 0, 0       # 慢指针, 快指针
        total = 0               # 连续子数组元素之和
        nums_len = len(nums)    # 数组长度
        min_len = nums_len + 1  # 初始化最小连续子数组长度
        
        ## 关键部分
        while slow < nums_len:
            if (fast < nums_len) and (total < s):  # 用元素累加, 而不用切片求和
                total += nums[fast]
                fast += 1  # 快指针后移一位
            else:
                total -= nums[slow]
                slow += 1  # 慢指针后移一位
 
            if total >= s:
                min_len = min(min_len, fast-slow)  # 每当子数组之和大于s就比较最小长度
 
        if min_len == nums_len + 1:
            return 0
        else:
            return min_len

        '''  遍历所有情况将在数量很大的时候超时
        for win in range(1, len(nums)+1):  # 滑动窗口递增
            for i in range(len(nums)):  # 本窗口移动次数
                if sum(nums[i:i+win]) >= s:
                    return win
        return 0
        '''

法二：对法一稍作优化，本质思想一致。将最小连续子数组长度 res 初始化为正无穷大，同时将快指针 end 自然地整合到 for loop 中从而减少一个类变量的调用与维护。

2020/06.18 - 99.80% - 最佳方法！

class Solution(object):
    def minSubArrayLen(self, s, nums):
        if not nums:  # 特殊情况
            return 0
        
        nums_len = len(nums)  # 数组长度
        start = 0             # 慢指针
        total = 0             # 连续子数组元素之和
        res = float('inf')    # 初始化最小连续子数组长度为﹢∞
        
        for end in range(nums_len):  # 快指针后移
            total += nums[end]       # 累加快指针所指元素
            while total >= s:                # 每当子数组之和 total > s
                res = min(res, end-start+1)  # 就比较一次最小长度值
                total -= nums[start]         # 减去慢指针所指元素
                start += 1                   # 慢指针后移
                
        if res == float('inf'):
            return 0
        else:
            return res