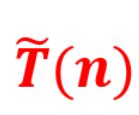计算机算法设计与分析 第4版 (王晓东) 重点题

第一章 算法概述

算法

• 算法是由若干指令组成的有序序列
• 输入：0个或多个
• 输出：至少一个
• 确定性：每条指令是清晰的、无歧义的
• 有限性：执行次数、执行时间有限

程序

• 算法用某种程序设计语言的具体实现，可以不满足算法的性质(4)有限性。

算法的复杂性

• 算法的复杂性是算法运行所需要的计算机资源的量
• 时间复杂性：需要时间资源的量
• 空间复杂性：需要空间资源的量

复杂性的渐进表达式

• 是T(n)的渐近性态（n->无穷大），为算法的渐近复杂性。
• 略去低阶项所留下的主项

O 符号的定义

• O评估算法的复杂性，得到的是当规模充分大时的一个上界。
• Ω得到的只是该复杂性的一个下界
• θ 同阶。f(N)=θ(g (N))，当且仅当f(N)=O(g(N))且f(N)=Ω(g(N))
• o：如果对于任意给定的ε>0，都存在正整数n0，使得当n≥n0时有f(n)/g(n)<ε，则称函数f(n)当n充分大时的阶比g(n)低，记为f(n)=o(g(n))

习题

1-1求下列函数的渐近表达式

• $3n^2$ +10n = O($n^2$)

• $n^2$ / 10 + $2^n$ = O($2^n$)

• 21 + 1 / n = O(1)

• log$n^3$ = O(logn)

• 10log$3^n$ = O(n)

1-2 试论O(1)和O(2)的区别

• 根据符号O的定义易知O(1) = O(2),用它们表示同一个函数时，差别仅在于其中的常数因子

1-4 假设某算法在输入规模为n时的计算时间为

1. 题目：假设某算法在输入规模为n时的计算时间为T=3*2n(2的n的次方）.在某台计算机上实现并完成该算法在t秒.现有另一台计算机,其运行速度为第一台的64倍,那么在这台新机器上用同一算法在t秒内能解输入输入规模为多大的问题?

   • 设新机器的规模是n1
   • T = 3 * $2^n$ = 3 * $2^n$${}^1$ / 64
   • n1 = n + 6 故新机器能解输入规模为n + 6的问题

2. T(n) = $n^2$

   • T = $n^2$ = $n{1}^2$ / 64
   • n1 = 8n

3. T(n) = 8

   • 由于T(n)是常数，因此可以解决任意规模的问题

1-5 硬件厂商XYZ公司宣称他们最新研制的微处理

• n1 = 100n
• $n{1}^2$ = 100$n^2$ ---- n1 = 10n
• $n{1}^3$ = 100$n^3$ ---- n1 = 4.64n
• n1! = 100n! ---- n1 = n + log100 = n + 6.64

1-8下面的算法段用于确定n的初始

• 下界为Ω(logn)
• 上界至今未知

1-1统计数字问题(简答题）

• 题目：一本书的页码从自然数1开始顺序编码直到自然数n。书的页码按照通常的习惯编排，每个页码都不含多余的前导数字0。例如，第6页用数字6表示，而不是06或006等。对给定书的总页码n，计算出书的全部页码中分别用到多少次数字0，1，2，…，9。

• 

• 看不懂上面的可以通过代码理解：老师的代码。

  #include 
  #include 
  #include 
  
  long num;
  long tab1[10] = {0, 1, 20, 300, 4000, 50000, 600000, 7000000, 80000000, 900000000};
  long tab2[10] = {0, 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000};
  long result[10];
  int flag = 0;   
  
  void compute (long x)
  {
     int len, i, high;
     long y;
     char string[10]; 
     sprintf(string,"%d",x);
     //len = strlen (itoa(x, string, 10));
     len = strlen (string);
     high = string[0] - 48;
     if (len == 1)
     {
         for (i = 0; i <= x; i++)
         {
             result[i] += tab1[len];
         }
         if (flag == 0)
         {
             result[0] -= tab2[len];
         }
         return;
     }
     else
     {
         for (i = 0; i <= 9; i++)
         {
             result[i] += tab1[len - 1]*high;
         }
         if (flag == 0)
         {
             for (i = 1; i < len; i++)
             {
                 result[0] -= tab2[len - i];
             }
             //flag = 1;
         }
         for (i = 0; i < high; i++)
         {
             result[i] += tab2[len]; 
         }
         if (flag == 0)
         {
             result[0] -= tab2[len];
             flag = 1;
         }
         for (i = 1; string[i] == 48 && len - i > 1; i++)    
             result[0]++;
         y = x - high*tab2[len];
         result[high] += (y + 1);
         compute (y);
     }
  }
  
  int main ()
  {
     int i;
     //freopen ("count.in", "r", stdin);
     //freopen ("count.out", "w", stdout);
     scanf ("%ld", &num);
     compute (num);
     
     for (i = 0; i<10; i++)
     {
         printf ("%ld\n", result[i]);
     }
     return 0;
  }
  

#include 
#include 
#include 

long num;
long tab1[10] = {0, 1, 20, 300, 4000, 50000, 600000, 7000000, 80000000, 900000000};
long tab2[10] = {0, 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000};
long result[10];  
void compute (long x)
{
   int len, i, high;
   long y;
   char string[10]; 
   sprintf(string,"%d",x);
   len = strlen (string);
   high = string[0] - 48;
   if (len == 1) {
   		for (int i = 0 ; i <= x; i++) {
   			result[i] += tab1[len];	
		}
   } else {
   		//1.先加上 high * tab1[len - 1]
	   	for (int i = 0 ; i <= 9; i++) {
   			result[i] += tab1[len - 1] * high;	
		}	  
		//2.加上 tab2中的数
   		for (int i = 0; i < high; i++) {
   			result[i] += tab2[len];	
		} 
		//3.加上y 和x本身的0 
		for (int i = 1; i < len - 1; i++) {
			if (string[i] == '0')result[0]++;
		}
		y = x - high * tab2[len];
		result[high] += y + 1;
		compute(y);
   }
}

int main ()
{
   int i;
   scanf ("%ld", &num);
   compute (num);
   char string[10]; 
   sprintf(string,"%d",num);
   int len = strlen (string);
   //减去一次多算的的0
   for (int i = 1; i < len; i++) {
   		result[0] -= tab2[i];
   } 
   result[0] -= tab2[len];
   for (i = 0; i<10; i++)
   {
       printf ("%ld\n", result[i]);
   }
   return 0;
}

第二章 递归与分治策略

递归

• 直接或间接地调用自身的算法称递归算法
• 用函数自身给出定义的函数称递归函数

分治法

• 将一个规模为n的问题分解为K个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解

二分搜索

大整数的乘法

习题

2-1 证明Hanoi塔问题的递归算法

• 

2-2下面的7个算法与本章中的二分搜索算法BinarySearch

2-3 设a[0:n-1]是已排好序的数

void binarySearch(int a[], int n, int x, int &i, int &j) {
	int left = 0, r = n - 1;
	while (left <= r) {
		int mid = (left + r) / 2;
		if (x == a[mid]) {
			i = j = mid;
			return;
		} else if (x > a[mid]) {
			left = mid + 1;
		} else {
			r = mid - 1;
		}	
	}
	i = r;
	j = left;
}

2-1 众数问题

#include 
#include 
using namespace std;
int n, num;
int main() {
    map<int, int> mp;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &num);
        mp[num]++;
    }
    int max = 0;
    for (map<int, int>::iterator it = mp.begin(); it != mp.end(); it++) {
        if (max < it->second) {
            num = it->first;
            max = it->second;
        }
    }
    printf("%d\n%d", num, max);
    return 0;
}

2-3 半数集问题

#include 
using namespace std;
int rec[10005];
void set(int n, int cnt) {
	rec[cnt] = n;
	for (int i = cnt; i >= 0; i--) {
		cout << rec[i];
	}
	cout << endl; 
	for (int i = 1; i <= n / 2; i++) {
		set(i, cnt + 1);
	}
}
int main() {
	int n;
	cin >> n;
	set(n, 0);
	return 0;
}

第三章 动态规划

基本思想

• 将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解
• 与分治法区别：子问题往往不是互相独立的
• 用表记录所有已解决的子问题的答案，在需要时再找出已求得的答案，这样就可以避免大量的重复计算

矩阵连乘

• 题目：对于给定的3个矩阵{A1， A2，A3} ，维数分别为10×100，100× 5和5×50，如何确定计算矩阵连乘积A1 A2A3的一个计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。

• 设计dp[i][j]: 保存第i~第j个矩阵数乘最少的结果（按照某种方式排列求出的最小次数）
• 设计s[i][j]: 来保存第i个矩阵~第j个矩阵根据那个中间地方进行划分
• dp[i][j] = min(dp[i][k] + dp[k+1][j] + 第i个矩阵的行 * 第k个矩阵的列 * 第j个矩阵的列， dp[i][j])
• 如果上面的式子进行更新了，代表当前k位置更优，那么s[i][j] = k;

for (int len = 2; len <= n; len++) { //区间长度
	for (int i = 1; i + len - 1 <= n; i++) {
		int j = i + len - 1; 
		for (int k = 1; k < j; k++) {
			dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + 第i个矩阵的行*
			第k个矩阵的列*第j个矩阵的列); //后面的值就= (pi-1 * pk * pj)
		}
	}
}

动态规划的基本要素

• 最优子结构
  • 当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构的性质。
• 重叠子问题
  • 子问题的重叠性质

最长公共子序列

• 设计dp[i][j] :存储第一个串的前i个字符和第二个串的前j个字符的最长公共子序列的长度

• 设计c[i][j]: 记录状态是由哪一个子问题得来的。1表示由dp[i-1][j-1]得来，2表示由dp[i - 1][j]得来，3表示由dp[i][j-1]得来。

• void LCS(int n, int m, char x[], char y[], int c[][], int dp[][]) {
      //初始化
      for (int i = 1; i <= n; i++) dp[i][0] = 0;
      for (int j = 1; j <= m; j++) dp[0][j] = 0;
      for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= m; j++) {
              if (x[i] == y[j]) {
                  dp[i][j] = dp[i - 1][j - 1] + 1;
                  c[i][j] = 1;
              } else if (dp[i - 1][j] >= dp[i][j - 1]) {
                  dp[i][j] = dp[i - 1][j];
                  c[i][j] = 2;
              } else {
                  dp[i][j] = dp[i][j - 1];
                  c[i][j] = 3;
              }
          }
      }    
  }
  

习题

3-1 最长单调递增子序列

• 设计dp[i]: 代表以a[i]为结尾元素的最长递增子序列长度. 序列a的最长递增子序列的长度就为max{b[i], 0<=i

• void LIS(int dp[], int a[], int n) {
      dp[0] = 1; //初始化
      for (int i = 1; i < n; i++) {
          dp[i] = 1;
          for (int j = 0; j < i; j++) {
              if (a[i] >= a[j] && dp[i] < dp[j] + 1) {
                  dp[i] = dp[j] + 1;
              }
          }
      } 	   
  }
  

3-1 独立任务最优调度问题

• 设计dp[i][j]:表示完成i个任务，A机器花费时间为j的条件下B机器花费的最少时间。

• #include 
  #include 
  #include 
  using namespace std;
  const int N = 1e3 + 5;
  int n, a[N], b[N], ans, sum, dp[N][N];
  void f() {
  	memset(dp, 0x3f, sizeof(dp)); 
  	dp[0][0] = 0; 
  	for (int i = 1; i <= n; i++) {
  		for (int j = 0; j <= sum; j++) {
  			if (j >= a[i]) {
  				dp[i][j] = min(dp[i - 1][j - a[i]], dp[i - 1][j] + b[i]);
  			} else {
  				//只能B机器做
  				dp[i][j] = dp[i - 1][j] + b[i]; 
  			}
  		} 
  	}
  	//找出最小的值 
  	ans = 0x3f3f3f3f;
  	for (int i = 0; i <= sum; i++) {
  		int t = max(i, dp[n][i]); 
  		ans = min(ans, t);
  	} 
  } 
  int main() {
  	cin >> n;
  	for (int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
  	for (int i = 1; i <= n; i++) cin >> b[i];
  	f();
  	cout << ans << endl;
  	return 0;
  }
  

第四章 贪心算法

基本思想

• 贪心算法总是作出在当前看来是最好的选择。贪心算法并不从整体最优考虑，只是某种意义上的局部最优选择

基本要素

• 贪心选择性质
  • 指所求问题的整体最优解可以通过一系列局部最优的选择即贪心选择来达到
• 最优子结构性质
  • 当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质

会场安排

• 按照开始时间从小到大进行排序。
• 优先队列里面保存的是每个会场的最后结束时间。每次出来的就是结束时间最短的，若这个新的活动的开始时间还是小于这个最短的，那么只能重新开一个会场。否则更新这个会场的结束时间。
• 最后队列里面数的个数就是会场个数。

#include 
#include 
#include 
#include 
using namespace std;
const int N = 10005;
struct Node {
	int s, e;
	bool operator < (const Node& w) const {
		return s < w.s;
	}
}p[N];
int n;
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &p[i].s, &p[i].e);
	sort(p + 1, p + 1 + n);
	priority_queue<int, vector<int>, greater<int> > q;
	for (int i = 1; i <= n; i++) {
		if (q.empty()) {
			//直接开一个
			q.push(p[i].e); 
		} else {
			int t = q.top();
			if (p[i].s > t) {
				q.pop();
			}
			q.push(p[i].e);
		}
	}
	printf("%d\n", q.size());
	return 0;
} 

上课讲述代码：

#include  
using namespace std;
template <class Type>
void GreedySelector(int b,int n,Type s[],Type f[],bool A[])
{
	A[b]=true;
	int j=b;
	for(int i=b+1;i<=n;i++)
		if(!A[i] && s[i]>=f[j])
		{
			A[i]=true;
			j=i;
		}
}

int main()
{
	int n=5;
	int s[n+1]={0, 1,12,25,36,27};
	int f[n+1]={0,23,28,35,50,80};
	bool A[n+1];
	int j=0;
	for(int i=1;i<=n;i++)
		if(!A[i])
		{
			GreedySelector(i,n,s,f,A);
			j++;
		}			
	cout<<j;			
	return 0;
}

最优装载

• 题目：有一批集装箱要装上一艘载重量为c的轮船。其中集装箱i的重量为wi。最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。
• 将重量进行排序，从最小的开始装。

单源最短路径问题

• https://blog.csdn.net/qq_41280600/article/details/103099005

习题

4-1 假定要把长为l1，l2，…，ln的（简答题）

• 按照l1 <= l2 <= … <= ln次序来考虑
  • 证：取{l1, l2, l3} = {1, 3, 4}， 按照题目所给的想法得出 A = {1，4} B = {3} 最大值是5
  • 若令A = {1, 3} B = {4}， 最大值为4。 这种方案更优 故得证
• 按照l1 >= l2 >= … >= ln次序来考虑
  • 证：取{l1, l2, l3, l4, l5} = {10, 9, 8, 6, 5}, 得出A = {10, 6, 5} B = {9, 8} 最大值为21
  • 若令A = {10， 9} B = {8, 6, 5} 最大值19。更优 故得证
• 正确方法：
  

4-2 将最优装载问题的贪心算法推广到2艘船的

• 不能产生最优解，不具备最优子结构性质
• 所以可以进行搜索求解

第五章 回溯法

基本思想

• 从开始结点出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。

  如果在当前的扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。换句话说，这个结点不再是一个活结点。此时，应往回移动至最近的一个活结点处，并使这个活结点成为当前的扩展结点。

子集树与排列树

• 当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。
• 当所给的问题是确定n个元素的满足某种性质的排列时，相应的解空间树称为排列树

装载问题

• 有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且∑1_(i=1)^n▒w_i ≤c_1+c_2

• 装载问题要求确定是否有一个合理的装载方案可将这n个集装箱装上这2艘轮船。如果有，找出一种装载方案。

• void backtrack(int i)
  {//搜索第i层结点
  	if(i>n) {//到达叶结点
  	    if(cw>bestw) bestw=cw;   
  	    return;  
  	}
  	//搜索子树
  	r -=w[i];
  	if(cw+w[i]<=c) 
  	{ //搜索左子树
  	    x[i]=1；//可行，装载集装箱i
  	    cw+=w[i]；//更新当前装载量
  	    backtrack(i+1)；//搜索第i+1层结点
  	    cw-=w[i];  
  	}
      if(cw+r>bestw) //进行剪枝 若不选这个而去  
      { //搜索右子树
          x[i]=0; 
          backtrack(i+1);  
      }
      r+=w[i]; 
  }
  

习题

5-1 装载问题改进回溯法1

void backtrack(int i)
{//搜索第i层结点
	if(i>n) {//到达叶结点
	    if(cw>bestw) bestw=cw;   
	    return;  
	}
	//搜索子树
	r -=w[i];
	if(cw+w[i]<=c) 
	{ //搜索左子树
	    x[i]=1；//可行，装载集装箱i
	    cw+=w[i]；//更新当前装载量
	    backtrack(i+1)；//搜索第i+1层结点
	    cw-=w[i];  
	}
    if(cw+r>bestw) //进行剪枝 若不选这个而去  
    { //搜索右子树
        x[i]=0; 
        backtrack(i+1);  
    }
    r+=w[i]; 
}

5-1 子集和问题

#include 
const int N = 10005;
int a[N], n, m, rec[N]; 
bool ok;
void dfs(int start, int sum, int cnt) {
	if (sum > m) return ;//剪枝 
	if (sum == m) {
		for (int i = 0; i < cnt; i++) printf("%d ", rec[i]);
		ok = true;	
		return ;
	}
	for (int i = start; i <= n; i++) {
		rec[cnt] = a[i];  //记录当前选的值 
		dfs(i + 1, sum + a[i], cnt + 1); //对下一个进行搜索 
		if (ok) return;
	}
}
int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
	}
	dfs(1, 0, 0);
//	if (!ok) printf("Solution！"); 
	return 0;
} 

第六章 分支限界法

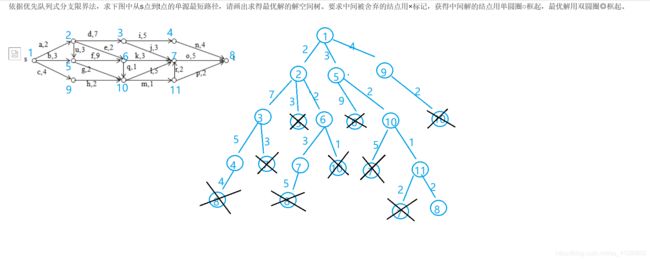
分支限界的基本思想

• 常以广度优先或以最小耗费优先的方式搜索问题的解空间树
• 在搜索问题的解空间树时，活结点一旦成为扩展结点，就一次性产生所有儿子节点。在儿子结点中，那些不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点加入活结点表。此后，从活节点表中取下一个结点成为当前扩展结点，并重复上述结点扩展过程，一直持续到找到所需的解或活结点表为空。

最短路径