博弈论算法
文章目录
- 基本原理
- 基本知识
- 奇异局势(必败局势)
- BashGame:同余理论
- NimGame:异或理论
- WythoffGame:黄金分割
- 阶梯博弈
基本原理
那就是若有多个人进行博弈,假设他们都足够聪明(能力已经相当于计算机了),在他们都没有失误并采取最优策略后,一定有一个人胜出,在知道初状态及规则的情况下,求解最终必胜的初状态(即何人胜出)的一类问题的理论及方法。
基本知识
1.异或运算符( ^ ),异或是一种对于两个数的二进制数进行运算的逻辑运算符
同真同假为假,一真一假为真,即1^1=0,0^0=0,1^0=1。
2.定义两个状态,分别为N和P:
N代表Next-position,可以理解为先手必胜状态;
P代表Previous-position,可以理解为后手必胜状态(或为先手必败)。
3.N/P两个状态的关系:
(1)无法进行局面转移的状态为P;
(2)只要有一种转移方式能将局面变为P,则当前状态为N;
(3)任何转移方式都只能使局面变为N,则当前状态为P。
4. 黄金比例 φ=(sqrt(5)+1)/ 2
奇异局势(必败局势)
1.任何自然数都包含在一个且仅有一个奇异局势中。
2.任意操作都可将奇异局势变为非奇异局势。
3.采用适当的方法,可以将非奇异局势变为奇异局势。
BashGame:同余理论
-
巴什博奕:一堆n个物品,两人轮流取,每次取1至m个,最后取完者胜
比如10个物品,每次只能取1到5个,则先手方必赢 1.面对[1...5]个局面,必胜 2.面对多余5+1个局面,必输 3.如果可以使对手面临必输局面,那么是必赢局面 4.如果不能使对手面临必输局面,那么是必输局面 基础: 1, 2, ..., m是必赢局面, m+1是必输局面 递推:m+2,m+3, ...,2m+1是必赢局面,2m+2是必输局面 ... k(m+1)是必输局面,应该允许k=0,因为0显然也是必输局面 在必输局和必赢局中,赢的一方的策略是:拿掉部分物品,使对方面临k(m+1)的局面 例如上例中10个物品,只能拿1到5个,先手方拿4个即可,对手无论拿多少个,你下次总能拿完 如果物品数量随机,那么先手一方胜利的概率m/(m+1),后手方胜利的概率是1/(m+1) -
模板
void BashGame(int n,int m){
if(n%(m+1)==0) {
System.out.println("败");
}else {
System.out.println("胜");
}
- 例题:HDU2188
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int cc=sc.nextInt();
for(int c=0;c<cc;c++) {
int n=sc.nextInt();//目标值,需超过
int m=sc.nextInt();//每次最大捐款数
if(n%(m+1)==0) {
System.out.println("Rabbit");
}else {
System.out.println("Grass");
}
}
}
}
NimGame:异或理论
-
尼姆博弈: m堆n个物品,两人轮流取,每次取某堆中不少于1个,最后取完者胜
有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。 这种情况最有意思,它与二进制有密切关系,我们用(a,b,c)表示某种局势 首先(0,0,0)显然是奇异局势,无论谁面对奇异局势,都必然失败。 第二种奇异局势是(0,n,n),只要与对手拿走一样多的物品,最后都将导致(0,0,0)。 仔细分析一下,(1,2,3)也是奇异局势,无论自己如何拿,接下来对手都可以将其变为(0,n,n)的情形。 计算机算法里面有一种叫做按位模2加,也叫做异或的运算,我们用符号⊕表示这种运算,先看(1,2,3)的按位模2加的结果: 1 =二进制01 2 =二进制10 3 =二进制11 ⊕ ——————— 0 =二进制00 (注意不进位) 对于奇异局势(0,n,n)也一样,结果也是0。 任何奇异局势(a,b,c)都有a⊕b⊕c =0。 注意到异或运算的交换律和结合律,及a⊕a=0,: a⊕b⊕(a⊕b)=(a⊕a)⊕(b⊕b)=0⊕0=0。 所以从一个非奇异局势向一个奇异局势转换的方式可以是: 1)使 a = c⊕b 2)使 b = a⊕c 3)使 c = a⊕b -
结论:
对于nim游戏的某个局面(a1,a2,…,an),当且仅当a1^ a2 ^ …^ an = 0,当前位于必败点,当前局面称为奇异局面,所有非奇异局面都能转化为奇异局面。
所有非偏博弈都能转化为Nim博弈。 -
证明
(1)无法移动的局面为所有石堆的石子数都为0,0 ^ 0 ^ …^ 0 = 0,显然已经输了;
(2)若当前的局面不为0,即a1 ^ a2 ^ a3 ^ … ^ an = k,则改变ai的值为aci = ai ^ k,能使得a1 ^ a2 ^ a3 ^ … ^ aci ^ … ^ an=0。
证明很简单,通过异或的性质,ai ^ k = a1 ^ a2 ^ a3 ^ … ^ ai ^ ai ^ … ^ an
ai ^ ai 将会被消去,即aci就是减去了ai这一堆的剩下的所有的异或,则此时
a1 ^ a2 ^ a3 ^ … ^ aci ^ … ^ an= a1 ^ a1^ a2 ^ a2 ^ a3 ^ a3 ^ … ^ an ^ an = 0
(3)若当前某个局面为P,即a1 ^ a2 ^ a3 ^ … ^ an=0,一定不存在改变某个ai,使之变为aci,使得a1 ^ a2 ^ a3 ^ … ^ aci ^ … ^ an = 0,因为aci = ai ^ 0 = ai,由题目可得不能不取,即当前的ai值必须改变,所以此时aci一定不等于ai。 -
模板
void Nim(int x[]) {
int sum = 0;
for (int i = 0; i < x.length; i++)
sum ^= x[i];
if (sum == 0)
System.out.println("必输");
for (int i = 0; i < x.length; i++) {
int k = sum ^ x[i];
if (k < x[i])
System.out.println("原堆个数为" + x[i] + "的子堆变为" + k);// 得出的结果为所有的方案第一次移动的数
}
}
- 例题:HDU1907
/*
**题目让求的是最后取光者为失败者,也就是说在取糖果的时候都要躲着最后一个糖果。
**首先来分析一下各种状态:
**假设S态表示异或和非0,T态表示异或和为0
**一堆糖果数量为1的称为孤独堆,否则称为充裕堆;Si或者Ti表示充裕堆的个数
** S0:表示有奇数个孤独堆,则先手必败;
** S1:表示有一个充裕堆,当孤独堆的个数为偶数时,先手只需要使得当前充裕堆只剩下一个即可
** 否则拿完即可,则先手必胜。
** T1:不存在这种状态,即不存在异或和为0且只有一个充裕堆的状态
** T0:表示有偶数个孤独堆。则先手必胜;
** S2:有两个以及以上的充裕堆,异或和非0;
** T2:有两个以上的充裕堆,异或和为0;
** 现在主要来分析下S2和T2态,从上面可知,S0先手必败,S1,T0先手必胜
** S2可以取一次变为T2。T2取一次可变为S2或者S1
** 因为S1是先手必胜态,根据这两个转换规则,我们就能得知S2也是先手必胜,T2是先手必败。
** 如果这道题是最后一个取的获胜,即完全的Nim博弈,就不需要特判1的个数了。
*/
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for (int T = 0; T < t; T++) {
int n = sc.nextInt();
int ans = 0, x = 0, sum = 0;
for (int i = 0; i < n; i++) {
x = sc.nextInt();
if (x == 1) {
sum += 1;
}
ans ^= x;
}
if (sum == n) {
if (sum % 2 == 0) {// 偶数个全1
System.out.println("John");
} else {// 奇数个全1
System.out.println("Brother");
}
} else {
if (ans != 0)
System.out.println("John\n");
else
System.out.println("Brother\n");
}
}
sc.close();
}
}
WythoffGame:黄金分割
-
威佐夫博弈:两堆(ak,bk)(ak<=bk)个物品,两人轮流取,每次从一堆中取不少于1个或者从2堆中同时取k个,最后面对(0,0)局面的输(设ak<=bk是为了忽略顺序的影响)
1.面对(0,0)局面必输 2.面对(1,1)(2,2)...(n,n)局面必赢 (0,1)(0,2)...(0,n)局面必赢 3.如果可以使对手面临必输局面,那么是必赢局面 4.如果不能使对手面临必输局面,那么是必输局面 基础:(0,0)是必输局面;(0,1)(0 ,2)...(0,n)是必赢局面, 递推:(1,2)是必输局面;(1,1)是必赢局面 (1,3)(1 ,4)...(1,n)是必赢局面 (2,2),(2,3)...(2,n)是必赢局面 (3,5)是必输局面;(3,3)(3,4)是必赢局面 (3,6)(3,7)...(3,n)是必赢局面 (5,5)(5,6)...(5,n)是必赢局面 (4,7)是必输局面;(4,4)(4,5)(4,6)是必赢局面 (4,8)(4,8)(4,9)...(4,n)是必赢局面 (7,7)(7,8)(7,9)...(7,n)是必赢局面 (6,10)是必输局面;(6,6)(6,7)(6,8)(6,9)是必赢局面 (6,11)(6,12)(6,13)...(6,n)是必赢局面 (10,10)(10,11)(10,12)...(10,n)是必赢局面 规律:(必输局面的规律比较容易找到) ak是前面必输局未出现的数中最小者, bk=ak+k( k=0,1,2,3,...n) 下面介绍必输局(奇异局)的最重要性质: 1,2,...,n中每一个自然数,出现且只出现在一个奇异局中。 推导:1.由于ak总是选择未出现的数,所以每个数总能出现在奇异局中 且ak不会选择到重复的数 2.bk=ak+k,所以bk总是比前面所有奇异局出现的数都大, 所以bk不会选择到重复的数 必赢一方的策略是:始终让对手面对必输局(奇异局势) -
证明:这里
-
给定任意局势(a,b),判定(a,b)是否为必输局势的方法是:
令 k=0,1…n
ak=[k * φ],bk=ak+k=[k * φ * φ]
如k=0,ak=0,bk=0
k=1,ak=1,bk=2
k=2,ak=3,bk=5
k=3,ak=4,bk=7 -
更好的一种判断策略是 k = b-a ,如a=k*φ时,当前局势为奇异局势
-
模板
void Wythoff(int a,double b){
double gold=(Math.sqrt(5)+1)/2;
int k=(a>b?a-b:b-a);
if(min==(int)(k*gold)) {
System.out.println("败");
}else {
System.out.println("胜");
}
}
- 例题:POJ1067
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
double gold=(Math.sqrt(5)+1)/2;
int a,b;
while(sc.hasNextInt()) {
a=sc.nextInt();
b=sc.nextInt();
int min=(a<b?a:b);
int k=(a>b?a-b:b-a);
if(min==(int)(k*gold)) {
System.out.println(0);
}else {
System.out.println(1);
}
}
sc.close();
}
}
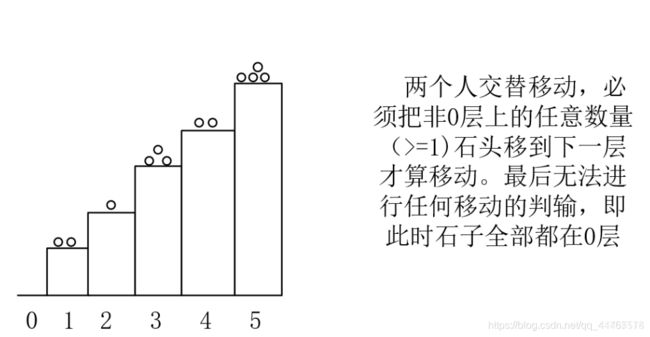
阶梯博弈
对奇数阶的石头进行 Nim,偶数阶的石头对结果不影响。
如上图:Nim和 = 2 ^ 3 ^ 4 = 5 不为 0,故先手必胜
把石头从奇数阶上移到偶数阶上相同于 Nim 中取一次石子。
为什么是奇数阶?
因为最后石子都要到 0 上,从 1 到 0 就是最后一步,这是从奇数阶到偶数阶,
所以认为从奇数阶上移到偶数阶上相当于取一次石子才能保证状态一致。
若 Nim和 != 0,先手将非 0 的局面转为 0 的局面,即把部分石子从奇数阶挪到下层偶数阶。
此时对手只有两种选择:
① 挪动奇数阶上的石头,从而打破了 0 的局面,再一次把非 0
的局面留给先手方,先手方继续调整奇数阶的石子即可。
② 挪动偶数阶上的时候到下层的奇数阶上,先手只要将这些刚挪下来的石子继续下挪,
这样奇数阶上的石子数量保持不变,又把 0 的局面留给对手。
这样一来,就能保证先手必胜了。
- 模板
void Nim(int[] nim){
int res = 0;
for (int j = 0; j < n; j += 2) {
res ^= Nim[j];
}
if(res==0) {
System.out.println("败");
}else {
System.out.println("胜");
}
}
- 例题:POJ1704
import java.util.Arrays;
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
int[] Nim,num;
for (int i = 0; i < T; i++) {
int n = sc.nextInt();
Nim = new int[n+1];
Nim[0]=0;
for (int j = 1; j <= n; j++) {
Nim[j] = sc.nextInt();
}
Arrays.sort(Nim);
int res = 0;
for (int j = n; j > 0; j -= 2) {
res ^= (Nim[j]-Nim[j-1]-1);
}
if(res==0) {
System.out.println("Bob will win");
}else {
System.out.println("Georgia will win");
}
}
sc.close();
}
}